積淀操作經驗 發展想象能力

在日常生活中，千姿百態的圖形美化了我們的現實世界，這些圖形既賦予了我們美的體驗，又為我們提供了諸多便利。同時也啟發我們去思考：圖形世界有哪些秘密？精美的物品都是由哪些基本圖形構成的呢？

一、圖形的由來

相傳四千年前，古埃及尼羅河每年都會洪水泛濫，泛濫的洪水在帶來肥沃淤泥的同時，也模糊了原有的土地界線．為了應對尼羅河洪水過后的土地界線問題，尼羅河流域的人們每年都會進行土地測量，因而，古埃及人積累了許多土地測量知識，也為幾何學的早期發展奠定了基礎．

我國對幾何學的研究歷史同樣悠久，我國新石器時代的黑陶器皿上的花紋演變逐漸由魚形過渡到不規則圖形，再到菱形、正方形等規則幾何圖形；墨翟及其弟子所著《墨經》里也有幾何圖形的相關知識；成書不晚于公元前2世紀的中國數學典籍《周髀算經》里記載了直角三角形三邊之間的關系；成書最遲在公元前1世紀的中國古代數學典籍《九章算術》里詳細記載了土地面積和物體體積的計算方法，此外，我國古代數學家祖沖之、劉徽等對幾何學的發展都做出了重大貢獻．

幾何圖形并不是數學家憑空創造的產物，而是由現實世界的實物抽象和提煉而來的．在現實世界中，存在著各種各樣的幾何圖形，包括簡單的幾何圖形，以及由簡單幾何圖形組成的復雜幾何圖形．

一些幾何圖形（如線段、角、三角形、長方形、圓等）的各部分都位于同一個平面內，它們是平面圖形，而有些幾何圖形（如長方體、正方體、圓柱、圓錐、球等）的各部分不都在同一個平面內，它們是立體圖形．

二、圖形的應用

幾何圖形的應用十分廣泛，尤其在創意文化用品和家居用品領域，幾何圖形扮演著重要角色，幾何圖形在幫我們解決生活問題的同時也美化了生活環境，現在我們提出一個問題：

能否利用手中的材料，制作一個正五棱柱呢？

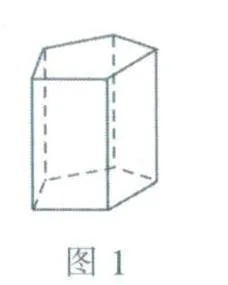
觀察正五棱柱（如圖1所示），可以發現正五棱柱的上表面和下表面是一樣的正五邊形．側面都是矩形，并且這些矩形都具有特定的性質：寬與正五邊形的邊長相等，長全部都相等，正五棱柱的展開圖需要滿足這樣的條件：上表面和下表面至少要有一條邊與側面連接，而側面之間則不必完全連接．

下面我們開始動手做．

（1）制作正五棱柱的展開圖，正五棱柱的展開圖大致分為兩類：

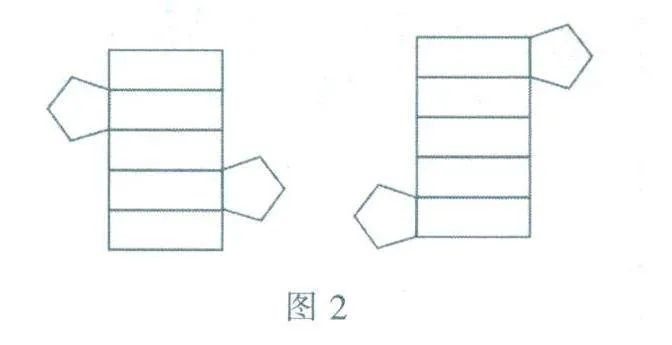
當側面都連在一起時，只要兩個一樣的正五邊形在側面所連成的大矩形的兩側即可（如圖2所示）.

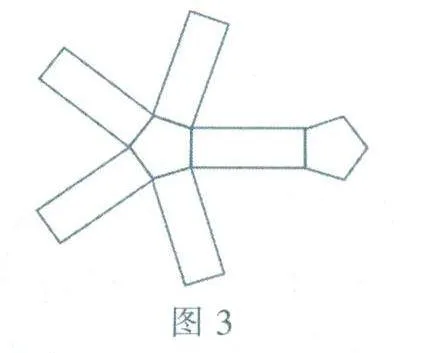
當側面和側面不連接在一起時，有一個正五邊形就會和每一個側面都相連，另一個正五邊形和其中的一個側面相連即可（如圖3所示）．

這兩類展開圖均可組成一個正五棱柱．

（2）任選第一步中可以組成正五棱柱的一個展開圖，將展開圖折疊起來，用膠粘好，一個正五棱柱就做好了．

三、圖形的學習

和數與代數、統計與概率領域的學習相比，幾何圖形領域的學習更需要在直觀操作和思考推理中完成．

1．動手實踐．

在本章中，教科書精心設計了豐富的數學實踐活動，許多數學結論和圖形的性質不是直接呈現給我們的，而是要求我們親自動手操作和探索，通過親身體驗，進而理解和掌握數學結論及圖形的性質．

2．細致觀察．

在幾何圖形的學習中，同學們需要學會如何從不同角度觀察和分析問題．在解決現實世界中的問題時，這是非常重要的技能．例如，在規劃一個花園時，同學們需要考慮如何最有效地利用空間，解決這樣的實際問題不僅使學習變得有意義，而且能幫助同學們認識到數學的重要性和實用價值．

3．激發想象．

數學學習離不開豐富的想象，尤其是幾何圖形的學習，更離不開想象，雖然本章提供了大量動手操作的數學活動，但是，我們不能完全依靠動手操作去探究所有的數學結論．

事實上，先想象一下，然后動手操作，再回想操作過程，是培養我們想象能力的重要環節．

4．學思結合．

“學而不思則罔”，在數學學習中，我們不能僅僅滿足于動手操作的活動層面，應該在操作的每個環節以及操作結束后進行深入思考：我是怎么進行操作的？為什么要這么做？這樣的操作方法是否有效？接下來我應該采取什么步驟？這個活動涉及哪些數學知識？通過這個活動我學到了什么？

總之，在“幾何圖形初步”學習中，多一次動手、多一分觀察、多一次想象、多一分思考，就會多一點收獲！

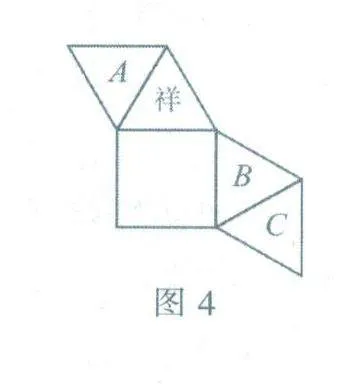
（2024年德陽）走馬燈，又稱仙音燭．史料記載，走馬燈起源于隋唐時期，盛行于宋代，是中國特色工藝品，常見于除夕、元宵、中秋等節日，在一次綜合實踐活動中，一位同學用如圖4所示的紙片，沿折痕折合成一個棱錐形的“走馬燈”，正方形做底，側面有一個三角形面上寫了“祥”字，當燈旋轉時，正好看到“吉祥如意”的字樣，則在A，B，C處依次寫上的字可以是（ ）．

A．吉、如、意

B．意、吉、如

C．吉、意、如

D．意、如、吉

參考答案：A