基于組合模型的安徽省農產品物流需求量預測

摘 要：農業生產者和供應鏈管理者要想合理制訂和調整生產計劃，就需要更加精準地預測農產品物流需求量。為了提高預測模型的擬合程度及預測結果的精確度，利用GM（1，1）結合BP神經網絡的組合模型，對安徽省未來5年的主要農產品物流需求量進行預測。首先，通過對傳統的GM（1，1）預測模型進行優化，構成預測的主體部分；其次，根據灰色關聯分析法，選取與安徽省農產品物流需求量關聯度最大的經濟指標，并建立相關的BP神經訓練網絡進行訓練和預測；最后，對GM（1，1）非線性殘差部分通過BP神經網絡進行優化，構建出無偏GM-BP組合預測模型，并對比幾種不同方式的預測結果。根據對比結果，組合模型的預測結果更加準確可靠。

關鍵詞：滑動無偏灰色模型；BP神經網絡；組合模型；農產品物流

中圖分類號：F224 文獻標志碼：A 文章編號：1674-7909（2024）8-46-5

DOI：10.19345/j.cnki.1674-7909.2024.08.009

0 引言

隨著我國農產品市場的不斷壯大和產業的快速發展，農產品物流發展的重要性也日益凸顯。一方面，農產品物流能夠促進農產品的流通和銷售，提高農產品的附加值，推動農村經濟的發展，促進農村地區的現代化建設；另一方面，農產品物流也能夠促進國際貿易和農產品出口，提高中國農產品在國際市場上的競爭力，推動中國農業的國際化進程。而農產品物流的穩定發展離不開對農產品物流需求量的預測。農產品物流需求量預測是指通過對農產品物流行業的市場環境、產品種類、交通運輸等因素進行分析，以預測未來一定時間內農產品物流需求的變化趨勢和數量規模。該預測可以為農產品生產、運輸和銷售等環節提供決策參考，支持物流企業的規劃和相關產業的發展。

很多學者研究提出了針對特定指標的預測方法。Wang X等［1］提出了一種基于粒子群優化的支持向量機（SVM）的房地產價格預測模型。Selakov A等［2］介紹了一種結合粒子群優化（PSO）和支持向量機（SVM）的混合方法，其可用于考慮溫度變化的短期負荷預測。Kisi O［3］探討了最小二乘支持向量機（SVM）和多元自適應回歸樣條（MARS）模型在長期河流水污染預測中的應用。Zou H F等［4］在多階段優化方法的基礎上，提出了一個短期食品價格預測神經網絡模型。Qi Fang［5］等通過組合模型對港口物流需求預測進行研究。

也有學者研究提出針對物流和冷鏈物流的預測模型。繆輝等［6］基于多元線性回歸模型對貴州省物流需求進行了預測。戎陸慶等［7］基于灰色理論的定量分析方法研究了區域果蔬冷鏈物流需求發展，為其發展過程所受到的環境因素影響提供了一種可行的范式。李思聰等［8］通過灰色—回歸組合模型對我國農產品冷鏈物流市場需求進行了預測。李捷等［9］提出了兩階段組合預測模型GSPS-BPNN，通過兩個不同階段、不同的模型對區域物流需求進行預測，證明其預測結果比單階段單一預測模型預測的結果更穩定。李國祥等［10］基于深度學習對物流需求預測模型進行了研究。岳偉等［11］利用灰色關聯法對各個影響因素指標進行分析，實現了對區域冷鏈物流需求量的預測，并且根據Shapley值法進行邊際貢獻分析［12］，對組合模型進行優化，提高了模型的預測優勢。李義華等［13］利用滑動無偏灰色預測模型對湖南省農產品冷鏈物流需求量進行了分析預測，發現滑動無偏灰色預測模型要優于傳統灰色預測模型。王曉平等［14］采用定性分析和定量統計相結合的方法研究農產品冷鏈物流需求的影響因素，建立了多種農產品冷鏈物流需求預測模型，并進行對比分析。

這些預測方法大多是單一模型，雖然準確率也比較高，但可能會出現過擬合或欠擬合或者無法適用于多種類型數據的情況，從而導致預測的結果并不準確。此研究在傳統灰色預測模型的基礎上進行優化改進，并與BP神經網絡相結合，不僅能夠有效改善過擬合或欠擬合的現象，還能提高預測模型的準確性，減小誤差。

1 影響因素的選取與分析

1.1 影響因素的選取

影響農產品物流需求的因素有很多，從宏觀角度來看，包括全球和國內的經濟增長水平、國際貿易環境、金融政策的變動，其都將影響農產品進出口，進而會直接或間接影響農產品物流。微觀因素包括農產品生產、供應、需求及政策等，都會對農產品的需求量產生影響。此次研究主要選取了與經濟水平、生產價格、物流量有關的因素。此研究以地區生產總值和第一產業增加值來代表供給水平的影響，以農產品生產價格指數、社會消費品零售總額、農林牧漁業總產值、國內外進出口總額來代表供給水平的影響，以貨物運輸量、鐵路運輸里程和公路運輸里程代表物流發展水平的影響，如表1所示。

1.2 灰色關聯度分析

為了探尋影響農產品物流需求的因素，收集包括地區生產總值、第一產業增加值、農產品生產價格指數、社會消費品零售總額、農林牧漁業總產值、國內外進出口總額、貨物運輸量、貨物運輸量、鐵路運輸里程、公路運輸里程的往年數據，運用Matlab計算出這些指標與安徽省農產品物流需求量的灰色關聯度值，并按照其關聯度值大小進行排序，得到表1。

表1可以看出各指標的關聯度值均大于0.5，說明文中選取的指標對安徽農產品物流需求的影響都是顯著的。

2 研究方法

此研究先對傳統的GM（1，1）預測模型進行優化，在傳統的GM（1，1）模型、新信息GM（1，1）模型和新陳代謝GM（1，1）模型中選擇最優模型的預測結果，將其作為GM（1，1）預測的主體部分；再選取與安徽省農產品物流需求量關聯度最大的經濟指標作為影響因素，并建立相關的BP神經訓練網絡，對數據集進行訓練和預測，構建出無偏GM-BP組合預測模型；最后，將幾種不同方式的預測結果進行對比，即可得到最優模型。

2.1 GM（1，1）灰色預測模型及優化

2.1.1 GM（1，1）模型

GM（1，1）表示的是模型是一階的，包含一個變量的灰色模型。GM（1，1）灰色預測的步驟如下：

①進行一階累加生成數據序列，見式（1）。

[x1k=m=1kx0m，k=1，2，…，n]" " " " " " " " " " "（1）

一次累加后的數據光滑比小于0.5的數據占比要大于60%。

GM（1，1）模型的微分方程見式（2）。

[dx1dt+aX1（t）=b] （2）

式（2）中：a為發展系數，b為灰作用量，利用一元線性回歸，即最小二乘法，求其估計值。

[a b=BTB-1BTYn]， （3）

B=[-12x11+x121-12x12+x131……-12x1n-1+x1n1]，[Yn=x02x03…x0n]" （4）

②建立生成數據序列模型，見式（5）。

[x1k+1=x01-bae-ak+ba，k=1，2，…，n]" （5）

③建立原始數據序列模型，見式（6）。

[ x01=x01]，

[x=x1k-x1k-1=1-e-ax01-bae-ak-1，]

[k=1，2，3，…，n] （6）

式（6）中：[x0k，k=1，2，…，n]為原始數據序列[x0k，]

[k=1，2，…，n]的擬合值。如果對原始數據進行預測，那么只需要滿足k≥n即可。

2.1.2 無偏灰色GM（1，1）模型

設無偏GM（1，1）模型的參數為[m]和[A]，則對原始序列見式（7）。

[x0k=Aemk-1，k=1，2，…，n]" （7）

通過一次累加可以得到式（8）。

[x1k=x0k=A1-emk1-em，k=1，2，…，n]" "（8）

參照傳統GM（1，1）建模方法可得式（9）。

[abT=BTB-1BTYn=21-em1+em2A1+em] （9）

因此，可以用傳統GM（1，1）模型參數a和b表示m和A的估計，見式（10）。

[m=ln2-a2+a，A=2b2+a]" " " " " " " " " " （10）

建立原始數據模型，見式（11）。

[x01=x01]；

[x0k=Aemk（k=0，1，2，…，n-1）]" " " " " " " " " " " " （11）

式（11）中：[x0k（k=0，1，2，…，n-1）]為原始數據序列的擬合值。

2.2 灰色預測模型精度檢驗

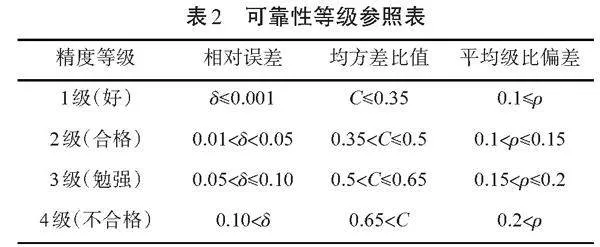
殘差檢驗一般包括殘差檢驗和后殘差檢驗，通過計算相對誤差、均方差比值和平均級比偏差的數值來判斷數據的精度等級，具體標準可參照表2。

2.3 BP神經網絡模型構建

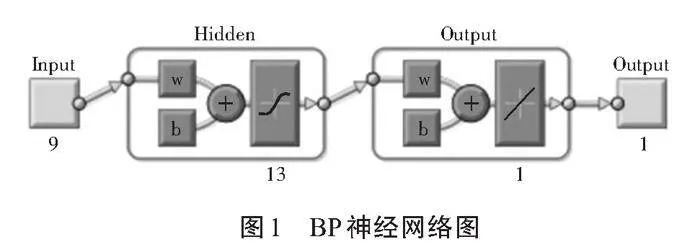
BP神經網絡的基本結構包括輸入層、輸出層和至少一個隱藏層。BP神經網絡的訓練過程可以分為前向傳播和反向傳播兩個階段。在前向傳播階段，輸入信號經過一系列的加權和非線性變換后，得到網絡的輸出。在反向傳播階段，根據網絡輸出與實際輸出之間的誤差，通過鏈式法則計算出每個神經元的誤差貢獻，并根據誤差貢獻來更新網絡的權重和偏置。BP神經網絡具有很強的非線性映射能力和柔性的網絡結構，可以適應各種復雜的非線性問題。網絡的中間層數、各層的神經元個數可根據具體情況而改變，并且隨著結構的改變其性能也有所不同。

3 實證分析

3.1 數據來源

此研究實證選取數據源自《安徽統計年鑒》《安徽省國民經濟和社會發展統計公報》，以及相關網站數據直接或間接得出。

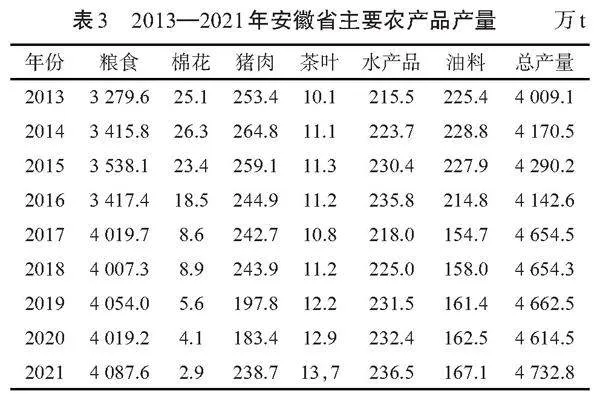
為了更加準確直觀地對特定地區的農產品物流需求總量進行描述和涵蓋，此研究將特定經濟區域的糧食、棉花、豬肉、茶葉、水產品、油料等農產品的產出總量均作為影響農產品物流需求總量的因素應用于預測模型，選取了2013—2021年的安徽省主要農產品產量作為原始數據，對安徽省未來5年主要農產品的物流需求量進行預測。通過統計年鑒，得到具體數據，見表3。

3.2 滑動無偏灰色GM（1，1）模型預測分析

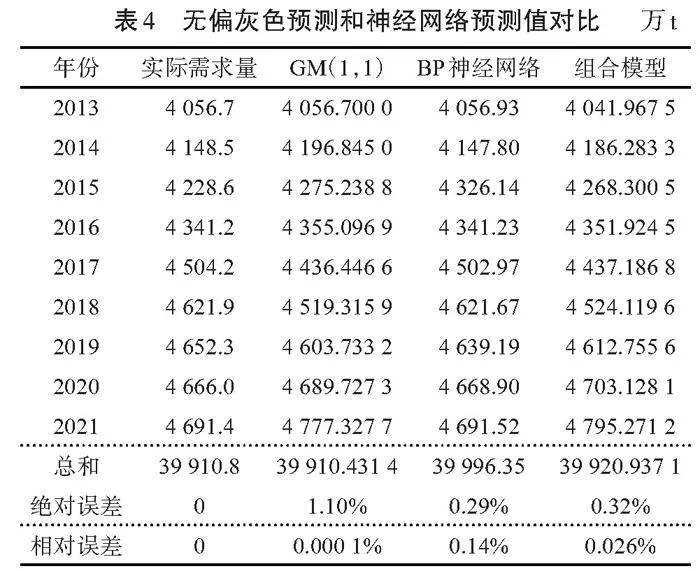
此研究以2013—2021年安徽省主要農產品產量為試驗數據，利用Matlab對農產品總量采用無偏灰色GM（1，1）模型進行預測，模型以最后3期為試驗組，前面的n[-]3期為訓練組，分別計算出傳統的GM（1，1）模型、新信息GM（1，1）模型和新陳代謝GM（1，1）模型的SSE值。選擇SSE值最小的模型作為最優模型對主要農產品未來5年的物流需求量進行預測，分析得到的預測值如表4所示。對預測得到的結果進行檢驗，小概率誤差精度檢驗結果等級為一級，平均相對殘差可靠性等級為二級，數據的均方差比值C=0.249 866 5≤0.35，可靠性等級為一級，說明該模型對原數據的擬合程度具有較高的準確性。因此，可以利用該預測結果作為無偏GM-BP 組合預測模型的線性主體部分。

3.3 BP神經網絡模型預測分析

根據關聯度分析所得到的數據可以看出，文中所選取的影響因素指標對安徽省主要農產品物流需求的影響是十分顯著的。因此，可以確定BP神經網絡（見圖1）的輸入神經元的數量為10個，通過神經網絡經驗公式kolmogorov定理：[h=m+n+a]可知，其隱層神經元個數應為5～14。經訓練集訓練檢驗，可以確定：其隱含層神經元數量為13個時，其回歸預測結果最好。

將影響農產品物流需求量的9個因素在2013—2021年的數據作為訓練集數據，建模后通過測試集對模型進行回歸預測性能檢驗，設置訓練次數為3 000次，最小誤差為0.000 001。模型訓練結果如表４所示。BP神經網絡預測結果總體R=0.996 63，具有較好的擬合度，得到的預測值如表4所示。

4 組合模型預測分析

從滑動無偏灰色GM（1，1）模型和BP神經網絡模型預測結果來看，滑動無偏灰色 GM（1，1）預測的總值與BP神經網絡預測總值相比更接近原始數據值，但個別數據的預測值與原始數據的偏差較大。而BP神經網絡預測總值雖然比無偏GM（1，1）預測的總值偏差大，但每個預測值與實際值的殘差都較小，對于整體預測來說更有利于準確判斷未來數據變化的趨勢。因此，可以將兩種方法結合起來組合成為無偏GM-BP組合模型，利用已經完善的BP網絡模型對無偏灰色GM（1，1）模型預測結果中得到的殘差項進行預測，然后將預測得到的殘差項與無偏灰色GM（1，1）模型預測得到的線性主體部分加和，得到組合模型的最終預測結果，并將3種預測模型的絕對誤差和相對誤差進行對比，結果如表４所示。

從結果來看，平均絕對誤差0.32%lt;1.1%，與無偏灰色 GM（1，1）模型和BP神經網絡模型相比，組合模型的擬合度和準確度更高。利用GM-BP組合模型對2022—2026年安徽省主要農產品物流需求量進行預測，得到結果如表5所示。

5 結束語

以2013—2021年的安徽省各主要農產品產量為原始數據，分別通過無偏GM（1，1）模型、BP神經網絡模型和無偏GM-BP組合模型等3種模型對數據進行分析和預測，探究最適用于安徽省主要農產品物流需求量預測的模型。從分析結果來看，無偏GM（1，1）模型總相對誤差最小，但絕對誤差偏差較大，而BP神經網絡模型的隨機性導致了試驗結果中個別數據存在較大偏差。因此，這兩種模型都不能完全適用于對安徽省主要農產品的物流需求量預測。

若能將兩種模型結合，取長補短，就能使兩種模型的優點相結合。因此，在無偏 GM（1，1）模型和BP神經網絡模型的基礎上，構成了新的無偏GM-BP組合模型，其克服了灰色預測模型預測的數據需要滿足一定規律性和趨勢性，以及BP神經網絡容易陷入局部最優解和數據量較少時產生的過擬合現象的缺點。將原始數據代入3種不同GM（1，1）模型中進行預測，選擇最優模型的預測結果，得到與原始數據的殘差后，利用BP神經網絡重新訓練，然后與無偏GM（1，1）模型預測的主體部分加和，得到最終結果。對比觀察可以發現，該組合模型預測精準度高于無偏GM（1，1）模型和BP神經網絡模型，所以此組合模型對安徽省2022—2026年主要農產品物流需求量進行預測的結果是相對較為準確的。

參考文獻：

［1］WANG X，WEN J，ZHANG Y，et al.Real estate price forecasting based on SVM optimized by PSO Optik-International［J］.Journal for Light and Electron Optics，2014，125（125）：1439-1443.

［2］SELAKOV A，CVIJETINOVIC D，MILOVIC L，et al.Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank［J］.Applied Soft Computing，2014，16（3）：80-88.

［3］KISI O，PARMAR K S．Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution［J］.Journal of Hydrology，2016，534：104-112.

［4］ZOU H F，XIA G P，YANG F T，et al．A neural network model based on the multi-stage optimization approach for short-term food price forecasting in China［J］.Expert Systems with Applications，2007，33（2）：347-356.

［5］FANG Q，TIG D.The model of highway logistic demand forecasting based on gray neural network［J］.Soft Science，2010（11）：132-135.

［6］繆輝，羅露璐.基于多元線性回歸模型的貴州省物流需求預測［J］.物流科技，2023，46（8）：75-78.

［7］戎陸慶，黃佩華.基于灰色理論的廣西果蔬冷鏈物流需求及其影響因素預測研究［J］.中國農業資源與區劃，2017，38（12）：227-234.

［8］李思聰，葉靜.基于灰色回歸模型的農產品冷鏈物流需求分析及預測［J］.公路交通科技，2022，39（5）：166-174.

［9］李捷，陳彥如，楊璐.基于兩階段組合預測模型的區域物流需求預測［J］.信息與控制，2018，47（2）：247-256.

［10］李國祥，馬文斌，夏國恩.基于深度學習的物流需求預測模型研究［J］.系統科學學報，2021，29（2）：85-89.

［11］岳偉.基于組合模型的區域冷鏈物流需求預測研究［D］.太原：太原科技大學，2023.

［12］岳偉，袁媛.基于Shapley組合模型的冷鏈物流需求預測研究［J］.赤峰學院學報（自然科學版），2023，39（8）：27-33.

［13］李義華，王沖，文哲，等.基于滑動無偏灰色模型的湖南省農產品冷鏈物流需求預測［J］.中南林業科技大學學報，2021，41（8）：161-168.

［14］王曉平，閆飛.京津冀農產品冷鏈物流需求影響因素及預測模型研究［J］.福建農業學報，2018，33（8）：870-878.

作者簡介：師小雨（1999—），女，碩士生，研究方向：農產品需求量預測。