精心設計問題　引導有效探究

　　(杭州市余杭區臨平第一小學，浙江杭州311100)
　　課堂提問是教師在教學時常用的方法之一，是每一位教師進行教學時必備的基本功，是實現教學目標的一種教學行為方式。經過教師精心設計的、有創造性的提問，能有效地引導學生進行探究活動。
　　
　　一、問題要有一定的開放性。給學生提供更大的探索空間
　　
　　教師在課堂提問中要把握好“度”，要難易適中。教師的提問不能像傳統教學的提問方式，一問一答，一答一個準，只提供一種可能答案，一種解決途徑，結果堵塞了學生的思路。教師的提問要符合學生的認知水平和實際生活經驗，給學生一定的探索空間。讓學生在問題的推動下展開多角度、多方向的思維活動。結合各方面的信息，在產生大量的答案的同時，獲得新奇、獨特的反應，從而培養思維的廣闊性和靈活性。
　　例如在學習“平移”時，教師在讓學生研究了什么是平移之后，出示了下圖：
　　
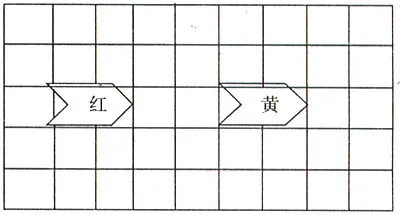
　　并讓學生圍繞“紅色的圖形到底要向右平移幾格才能和黃色圖形重合”這一問題進行研究。這一問題為學生提供了足夠的探索空間，也引發了孩子們強烈的探究欲望，學生的答案各不相同，有的孩子認為是2格，有的認為是4格，也有的認為是6格。“看來同學們的意見還不統一，你有辦法證明你的判斷是對的嗎?你的紙上也有這樣兩個圖形，先動手試一試，再把你的想法和你的同桌交流一下。”通過研究，學生得出了以下幾種方法：移動實物直接進行驗證；根據距離標上數；找對應點，從前面的尖點到尖點剛好是4格；加一加，圖形2格加上中間空格2格一共是4格。適度的問題空間引導學生進行探索，并且使思維得到提升，并不一定要進行操作。可以通過觀察得出平移距離。
　　又如在學習“分數的初步認識”時，為學生提供了這樣的問題：①同學們想不想自己動手平均分一分，得到一些分數呢?老師為每個四人小組都準備了一些平面圖形，你可以動手折一折，將這些圖形平均分，并把自己想要的分數涂上顏色。說一說你的分數是多少，是怎么來的。②觀察這些圖形和對應的分數，還有沒有其他的發現?
　　學生有了對1/2的體驗后，就能夠用類比的方法去創造更多的分數，于是教師就大膽地創設了用折紙和涂色的方法創造分數的活動，并讓學生上臺展示、解說自己的成果，讓學生有一次展示自己的機會。學生創造的分數是出乎意料的，不光有幾分之一，更多的是幾分之幾。教師通過這些現成的分數，讓學生的思維展開了一次又一次的碰撞：同樣的長方形，在平均分成2份的時候，得到的每一份的形狀不同，但是大小一樣，都可以用1/2來表示，讓學生體會到平均分成2份，取一份就是1/2(只跟平均分的份數和取的份數有關)；一個長方形的1/2和一個三角形的1/2大小和形狀完全不同，但都表示1/2，讓學生體會到了分數的相對性；甚至學生們還發現了同樣大小的一個圓，它的1/2與它的1/2的大小是一樣的。
　　
　　二、問題要有指向性，給學生提供一定的思維方向
　　
　　教師提出的問題要有針對性，要根據每節課的教學要求，針對教材的重點和難點，以及學生的原有認知設計問題，不能離開教學目標，漫無邊際地提一些問題。教師所提的問題情境并不神秘，是學生生活范圍中所感受到的，但又不能直接用自己已有的知識經驗加以處理。又熟悉又不能馬上解決，才產生疑惑，引發思考，促進探索。通過將已有知識信息重新組合，達到問題解決的目的。
　　如學習“認識人民幣”時，課的末尾向學生提出了這樣的問題：為什么人民幣的面值只有1角、2角、5角，1元、2元、5元……，而沒有3角、4角、6角、7角……?顯然這樣的問題學生不能用現成的知識直接回答，必須運用學到的知識進行假設、分析，重新組合才能解決。
　　又如在學習“簡單的條形統計圖”時，教師是根據這樣兩個問題展開教學的：學校要開展紅領巾超市活動，我們班決定賣“速食”，班主任王老師初步列出了四種食品供大家參考(貢丸、玉米、豆腐干、油炸臭豆腐)你認為我們賣哪一種比較合適?
　　生1：我覺得玉米好，我喜歡玉米。生2：貢丸，它還有湯可以喝。……
　　師：意見不統一怎么辦?生：統計一下，聽人數多的。師：怎么統計?
　　學生統計出了喜歡吃各種速食的人數情況：貢丸20人、玉米2人、豆腐干14人、油炸臭豆腐4人。
　　師：你們現在覺得應該賣哪一種了吧?
　　生：可以賣貢丸，也可以賣豆腐干……
　　師：用什么方式把你們的意見告訴你們的王老師呢?
　　生1：把統計結果告訴王老師。
　　生2：把統計的數據制成表格，并用文字說明后交給老師。
　　生3：可以把它制成統計圖。
　　師生接下去一起學習研究條形統計圖。
　　這樣的問題具有現實意義，又富有挑戰性。問題看似寬泛，但又有明確的思維指向：讓學生在4中食品中選擇；經過統計之后想到了制成統計圖，從而更進一步產生了制作統計圖的需求。
　　
　　三、問題要有突破性。根據學習進程及時追問或補問
　　
　　在課堂教學中，教師一開始的提問往往是啟發學生進行觀察，引導學生認知沖突，從中尋找解決問題的思路。那么當學生根據教師的提問進行探究的時候，或許會遇到一些問題，比如偏離正確的思考方向，或者對于問題的解釋帶有片面性，這就需要教師對這些問題進行追問，突破這一知識點，提高學生理解的水平。
　　如在學習“平均數”時創設了這樣的情境：
　　計算達標競賽，4(2)班的平均成績是89分，4(3)班的平均成績是95分；
　　1978年杭州市平均每人住房面積4平方米，1999年杭州市平均每人住房面積是9平方米；
　　師：你發現了什么?
　　生1：我發現4(3)班比4(2)班的平均成績高，高了6分；1999年杭州市平均每人住房面積比比1978年多了5平方米。
　　生2：我們的生活條件越來越好了，房子住的越來越大了。
　　生3：我覺得4(2)班同學的計算水平有點低。
　　師：是不是4(2)班每一個同學的計算水平都比較低，只有89分?
　　生1：不是的，這89分是平均數，是全班同學的總成績除以總人數得到的，并不是每一個同學的真正分數，有的可能比89分多，有的可能比89分少，有的可能剛好89分。
　　生2：9平方米也是一個平均數，并不是說每個人都只有9平方米，有的人家住著別墅，面積很大呢!
　　生3：平均數相當于是一個中間數，不大也不小，它只是說明了全班同學的學習情況。
　　教師提出問題讓學生解讀信息，其主要目的是通過解讀生活中的平均數，進一步理解平均數的意義，了解平均數在生活中的運用。教師提的第一個問題，十分寬泛，希望在這樣寬泛的問題中達成目標，但是學生看到了蘊藏在這些信息后面的一些人文性和教育性，對于平均數意義的理解還沒有顯示出來。于是教師教師進行了第二個問題的補問，這個問題引導學生思考平均數的意義，加深對平均數意義的理解。
　　我們經常可以看到教師根據學生的回答進行追問或補問：“這樣的思路可以嗎?為什么?”“再想想，還有別的想法嗎?”“你能理解××同學的思路嗎?”“你是怎樣想的，為什么這樣想?”……通常，開始的問題是啟發學生的觀察，引導學生的認知沖突，從中尋找解決問題的思路，那么在研究過程中的追問或補問，可以讓學生更加深入地理解概念的本質。
　　(責任編輯：張華