經濟類應用題的解法訓練

周成旻

《數學課程標準》指出:“讓學生人人學有價值的數學;人人都能獲得必需的數學;不同的人在數學上得到不同的發展。”學生是否獲得有價值的數學,判斷標準之一是能否運用數學知識解決實際問題。為考察學生解決實際問題的能力,許多教師選擇應用題進行測試。因此,應用題是初中數學教學中的重點,也是教學中的難點。

隨著我國經濟的發展,經濟問題逐漸呈現在我們面前。學生要適應社會需要,就應該掌握一些基礎的經濟知識,這不僅能擴大學生的視野,而且能提高學生運用數學知識解決實際問題的能力,對他們以后進入社會從事相關工作,也有益處。實驗人教版《數學》教材也增加了相關市場經濟的問題,主要以應用題的形式出現。解答此類問題的關鍵是將實際問題轉化為數學問題,通過對數學問題的求解得出實際問題的答案。現就常見的經濟類問題,通過下面的具體例子作些分析。

一、巧設輔元

例1有一商人需要進貨,若進價便宜8%,而售價保持不變,那么他的利潤(按進貨價而定)可由目前的x%增加到(x+10)%,x等于多少?

分析:本題數據很少,若直接列方程十分不易,可引入輔助元進貨價M,則0.92M是打折扣的價格,x是利潤。

解答:根據售價=進價×利潤+進價, 求出原來售價=M(1+x%),

現在售價=0.92M [1+(x+10)%],列方程得:

M(1+0.01x)=0.92M[1+0.01(x+10)]約去M,解之,得 x=15.

類似試題:現對某商品降價10%促銷,為了使銷售總金額不變,銷售量要比按原價銷售時增加百分之幾?

二、建立表格

例2從1999年11月1日起,全國儲蓄存款征收利息稅,稅率為利息的20%。某人在1999年12月存入人民幣1000元,定期一年,到期后將本息再存一年(和上年利率相同)。兩年后他共得1031.9 元。那么此項存款業務的年利率為多少?

分析:實際考察這個問題時,很多學生都分不清第二年存款的本金是多少。為了說明其中的數量關系,可建表格。設此項存款業務的年利率為x:

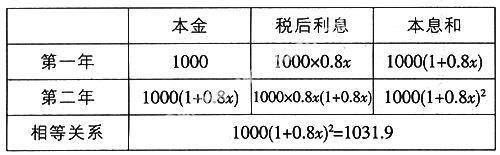
列方程得1000(1+0.8x)²=1031.9。解得x=1.98%。

說明:實際問題中的利率都是和銀行現行的利率一樣的,可讓學生收集銀行有關存款利息資料,進行閱讀分析,弄清有關的含義。然后根據自己的了解或與家長討論,進行編寫與儲蓄有關的題目,并寫出解答過程。之后,教師可進行評定,并適當地對題目的內容、條件或所求的結果進行擴充或修改。這種活動,溝通了實際模型與應用題之間的聯系,鍛煉了學生編寫應用題的能力,還能激發學生的對新知識的渴望。

三、構建函數模型

例3某商品每件60元,每星期賣出300件。如調整價格,每漲價1元,每星期要少賣10件。已知每件商品的成本為40元,如何定價才能使利潤最大?

分析:將實際問題轉化為函數模型問題,也就是我們俗稱的建模。用相關的函數知識確定最佳方案,進行數學上的計算。再用計算獲得的結果去解釋實際問題,即對實際問題總結做答。

解答:設上漲x元,利潤為y元,由題意得

y=(60+x-40)(300-10x)。化簡y=-10x²+100x+6000。

∵y=-10(x-5)²+6250, ∴ x=5。

所以定價為65元能使利潤最大化。

類似試題: 某書店有1000本書出租,每本書收2元時,可全部租出。若每本書提高0.5元,則減少100本書租出;若每本書再提高0.5元,則再減少100本書租出。為了獲利大,每本書應提高多少元?

四、利用隱含條件

例4某市按以下規定收取煤氣費:每月用煤氣不超過60m³,按每立方米0.8元收費;若超過60m³,按每立方米1.2元收費。某戶4月份的煤氣費平均每立方米0.88元,那么該用戶應交煤氣費多少元?

分析:由題意知用戶該月所用煤氣已超過60m³,設用戶該月用了x立方米煤氣,且x>60,則煤氣費可表示為60×0.8+1.2(x-60), 也可表示為0. 88x,所以60×0.8+1.2(x-60)= 0. 88x,求出煤氣立方數就可得解。

說明:解應用題的關鍵是找等量關系,需要通過分析才能得出,所以解題時要仔細審題挖掘出隱藏的條件。

經濟類應用題種類繁多,相應的變化層出不窮,解決這些問題的關鍵是掌握解應用題的基本方法,認真分析題目,找出其中的相等關系,那么這些問題都是能夠迎刃而解的。總之,我們在數學教學中要重視學生能力的培養,使學生獲得較高的應用數學知識解決實際生活、生產中問題的能力,以適應時代的需要。◆(作者單位:江西省德興市三○八學校)

□責任編輯:包韜略