采用Kalman濾波器進行信號處理的高頻信號注入法在電動機控制中的應用

鄭澤東 李永東 Maurice Fadel

（1. 清華大學電機工程與應用電子技術系 北京 100084 2. 法國圖盧茲國家理工學院ENSEEIHT LAPLACE-CNRS實驗室 圖盧茲 31071）

1 引言

無機械傳感器交流電動機控制技術是目前交流傳動領域研究的一個熱點。由于不需要機械傳感器，因而系統(tǒng)成本降低，結構簡單，減小了機械尺寸，提高了可靠性。無機械傳感器控制需要根據電壓和電流檢測結果來估算或者觀測轉速和位置，在低速下電動機中的電壓信號比較小，信號檢測誤差和噪聲等會給估算結果造成較大的誤差，因此低速問題是制約無機械傳感器電動機控制技術發(fā)展的一個瓶頸。特別是在零速附近，電動機基頻電壓幾乎為零，理論上如果不注入信號，傳統(tǒng)的無機械傳感器控制方案在零速附近會失效。高頻信號注入是解決這個問題的一個非常有效的方法，注入的高頻信號因其頻率足夠高，對轉速轉矩等產生的影響較小，而由于磁場飽和和凸極等因素的影響，注入的高頻信號會由于轉子位置的不同而產生不同的響應，所以通過檢測注入信號的響應就能夠得到轉子磁鏈位置的信息。

由于電動機通常采用逆變器控制，在檢測的信號中除了基頻信號和注入高頻信號的響應外，還有PWM 開關產生的各次諧波、外界干擾等，所以如何從電流中提取有用的信息，降低諧波和噪聲的影響是高頻注入法需要解決的一個重要問題。常用的方法是通過低通和帶通濾波器來提取信號，為了得到好的幅頻響應，需要采用一些特殊的濾波器，如切貝雪夫濾波器等，但是仍然無法避免會對信號幅值和相位產生影響，提取的信號中往往會含有頻率相近的諧波和噪聲信號，影響系統(tǒng)的性能[1-2]。

本文提出了一種用 Kalman濾波器來提取信號的高頻信號注入法。Kalman濾波器可以從含有多頻段諧波和噪聲的信號中提取特定頻率的信號，不會產生幅值和相位誤差，系統(tǒng)穩(wěn)定性較好。Kalman濾波器是一種自適應濾波器，從其被提出以來就廣泛應用于信號檢測和處理中，特別是在導航、定位等系統(tǒng)中[5-7]。本文以永磁同步電動機為例，通過仿真和實驗驗證了該方法的有效性，并且可以很容易地把該方法推廣到異步電動機等應用中。

2 高頻注入法原理

高頻信號注入法一般用在異步電動機或者永磁同步電動機無機械傳感器控制中，本文以永磁同步電動機為例進行說明。利用高頻注入法檢測轉子位置，要求轉子必須有一定的磁凸極，即要求定子繞組的電感是轉子位置的函數，所以一般應用在凸極電動機上。對于隱極電動機，隨轉子位置不同，定子繞組的磁飽和度存在差別，所以在繞組的飽和度不是太小的情況下高頻注入法在隱極電動機上也是適用的[1-2]。

在轉子磁場定向同步坐標系下，永磁電動機模型可以寫成如下形式

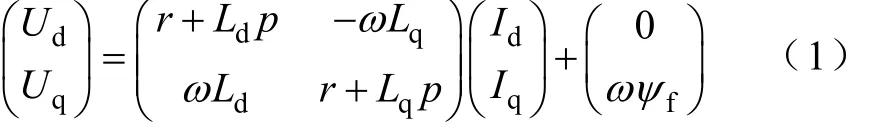
由于注入信號角頻率遠大于電動機轉子角速度，高頻信號方程中可以忽略交叉耦合項，高頻信號支路可以寫成如下形式

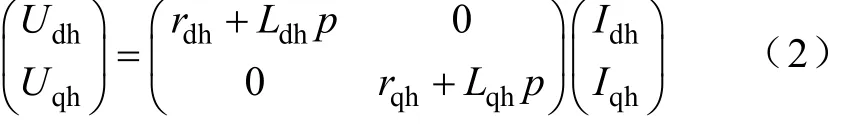
在無傳感器控制中，轉子磁鏈角度的估計值和實際值之間會存在一定的偏差，定義偏差為

式中Ud，Uq——電動機d、q軸電壓；

Id，Iq——電動機d、q軸電流；

Udh，Uqh——電動機d、q軸高頻電壓；

Idh，Iqh——電動機d、q軸高頻電流；

Ld，Lq——定子繞組d、q軸基頻電感；

Ldh，Lqh——定子繞組d、q軸高頻電感；

r——定子繞組電阻；

rdh，rqh——定子繞組 d、q軸高頻電阻，一般rdh=rqh；

ω——轉子電角速度；

ψf——轉子磁鏈幅值；

p——微分算子；

θ——轉子磁鏈的電角度。

在實際應用中，機端電壓一般用參考電壓來代替。用上標γ表示該變量是在由估計角度定向的同步坐標系下的值，跟實際值存在一個γ的角度偏差。

那么在以估計角度?θ定向的坐標系下，由式（2）可以得到

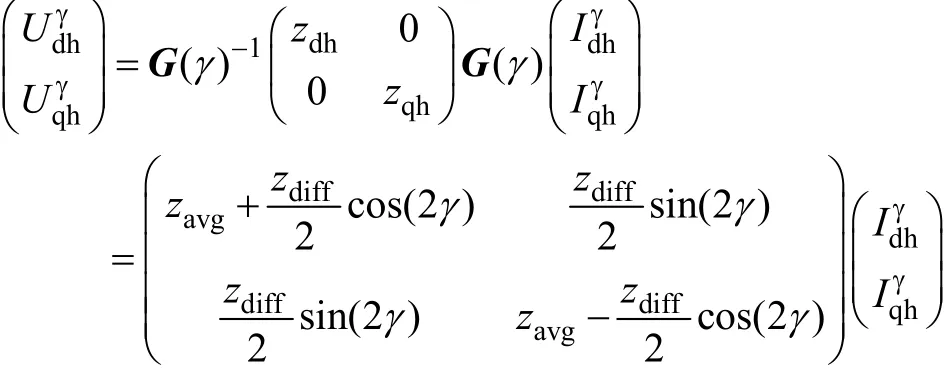
3 傳統(tǒng)信號提取處理方法

傳統(tǒng)方法中一般采用如下步驟處理信號：首先用一個帶通濾波器（BPF）從q軸電流信號中把高頻分量提取出來，然后把高頻分量乘以-sinωht，再用低通濾波器（LPF）提取式（9）中的第二項。

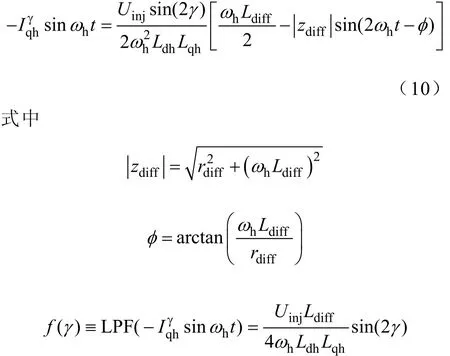
根據f(γ)，用一個PI環(huán)節(jié)就可以辨識出轉子轉速，然后積分得到轉子位置。傳統(tǒng)高頻注入法框圖如圖1所示。

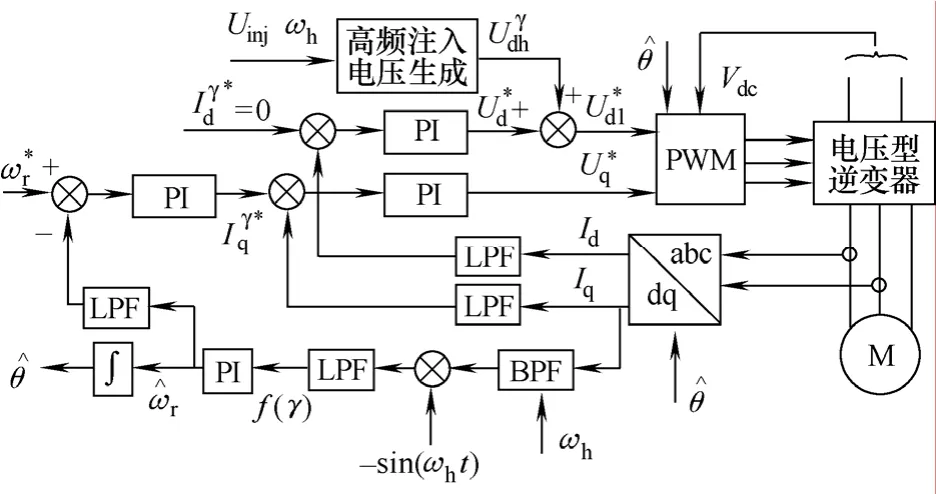
圖1 傳統(tǒng)高頻注入法框圖Fig.1 Traditional HF injection method

在施加高頻注入電壓后，dq軸電流中都會出現(xiàn)相應的高頻分量。因此在作為電流調節(jié)器輸入的反饋電流中應該把高頻分量去除，否則電流調節(jié)器會產生相應的響應來消除這些高頻分量，最終的結果是d，q軸參考電壓中也出現(xiàn)了對應的高頻分量來抵消高頻注入電壓。所以在dq軸電流上各施加一個低通濾波器來濾除高頻分量，然后作為電流調節(jié)器的反饋輸入量。

4 基于Kalman濾波器的信號處理方法

假設dq軸電流的測量值如下：

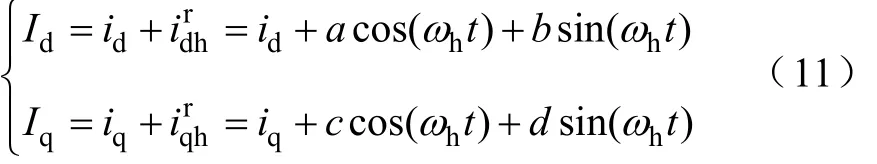
式中，id、iq為dq軸電流的基頻分量（直流分量）。

為了提高 Kalman濾波器對高頻分量的辨識能力，盡量在Kalman濾波器之前把dq軸電流中的基頻分量去掉，因此把dq軸電流減去dq軸電流的參考值后作為Kalman濾波器的輸入

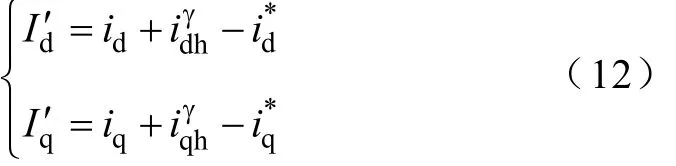
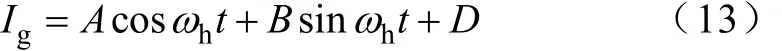
為了建立 Kalman濾波器模型，選擇電流中正弦分量的幅值，余弦分量的幅值和基頻分量為狀態(tài)變量

假設高頻分量的幅值和基頻分量變化緩慢，則離散方程可以寫成

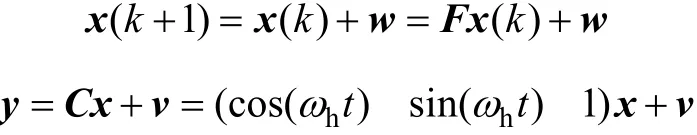
式中F——單位陣；

w——輸入噪聲（系統(tǒng)噪聲）；

v——輸出噪聲（測量噪聲）。

噪聲一般為平穩(wěn)的高斯白噪聲，平均值為零。噪聲的協(xié)方差矩陣定義為

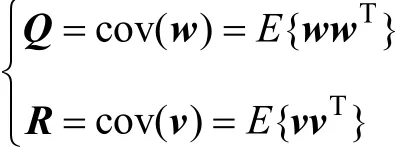
Kalman濾波器迭代過程如下：

（1）計算下一步的先驗估計值與相應的誤差

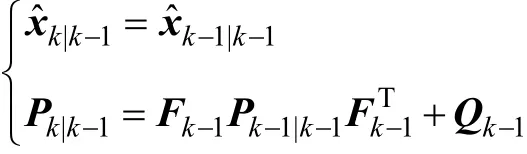
（2）計算Kalman增益

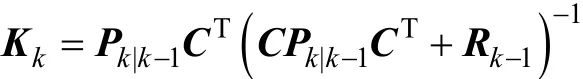
（3）從測量向量計算當前的最優(yōu)估計值

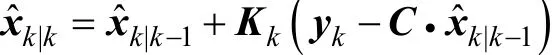
（4）計算當前最優(yōu)估計值的誤差

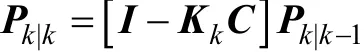
式中，矩陣P定義為估計值的誤差的均方；I為單位陣。

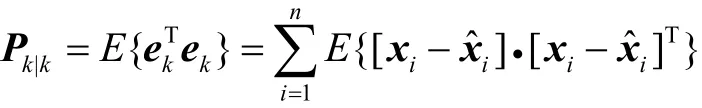
式中，E{·}代表求期望值[3-4]。

dq軸的Kalman濾波器的輸出分別為狀態(tài)變量的最優(yōu)估計值

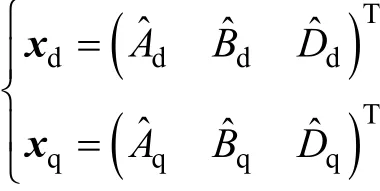
在其輸出端的基頻分量中再加上電流給定值得到dq軸電流基頻分量的最優(yōu)觀測值

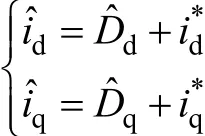
并把這個量作為電流調節(jié)器的反饋值。

根據q軸電流中的高頻分量的幅值（主要是正弦分量），通過模型參考自適應的方法來辨識轉子轉速和角度，在轉子角度估計誤差為零時，正弦分量的幅值應該為零。

一般可以用比例積分環(huán)節(jié)來實現(xiàn)轉速辨識，即

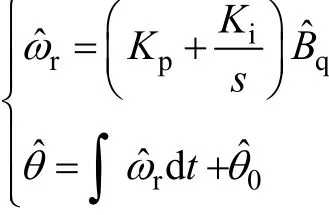
通常把估計的轉速再通過一個低通濾波器后作為轉速反饋值，以減少其中的噪聲。

由于噪聲特性位置，所以Q和R矩陣一般通過實際調試得到，調節(jié)Q、R矩陣的值，還可以在Kalman濾波器的輸出量中把電流測量中的噪聲去掉，得到測量電流的一個最優(yōu)估計值[5-7]。

在高頻注入法中，另外一個很重要的問題就是逆變器開關狀態(tài)的死區(qū)補償問題。最直接的死區(qū)補償方法是根據逆變器輸出的三相電流方向來進行，但是由于實際電流的測量值中常常含有很多測量噪聲，所以在電流的過零點附近常常會造成補償錯誤。因此一般把dq軸電流濾波，然后反變換到三相坐標系，把濾波后的電流值作為補償依據，這樣就避免了直接對相電流濾波造成的相移問題。但是在高頻注入法中，由于dq軸電路中仍然包含高頻的交流分量，所以在dq軸上進行濾波同樣會造成相位偏移。而Kalman濾波器通過合適的Q和R矩陣設置，可以很好地從dq軸電路中去除噪聲，并且不會產生相移。所以把經過Kalman濾波之后的dq軸電流的基頻分量和高頻分量的和如式（15），再變換回三相坐標系，作為死區(qū)補償的依據。

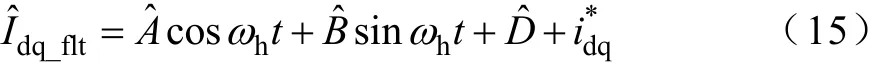
基于 Kalman濾波器的高頻注入法系統(tǒng)框圖如圖2所示。這里高頻注入電壓直接疊加在dq軸電壓的給定值上，然后作為 PWM的計算依據，即逆變器發(fā)出的電壓中就已經包含了注入的高頻電壓，所以不需要額外的高頻電源。

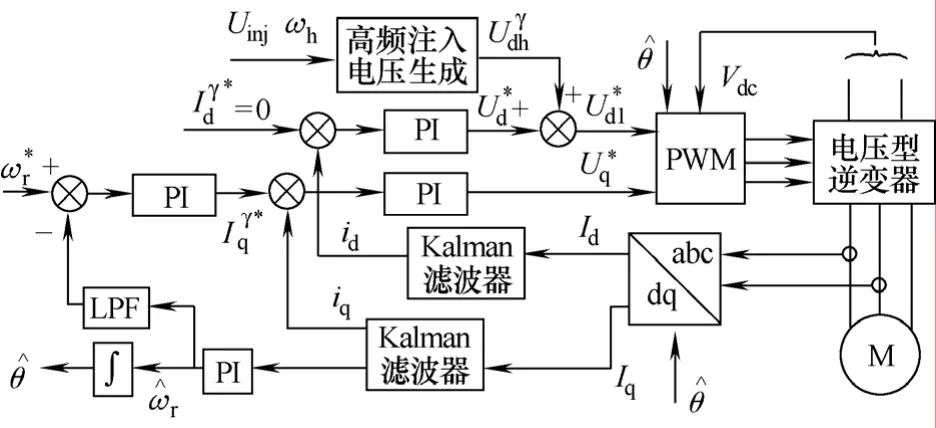
圖2 基于Kalman濾波器的高頻注入法框圖Fig.2 HF injection method based on Kalman filter

5 仿真結果

為了驗證上述算法的有效性，用 Matlab/Simulink進行了仿真驗證。仿真中，電動機dq軸電感分別為Ld=1.0mH，Lq=1.5mH，注入電壓幅值為20V，頻率為 500Hz。電動機采用轉子磁場定向矢量控制，d軸電流基頻分量控制為零。

電動機起動過程中，d軸電流中的基頻分量和高頻分量的分離結果如圖3所示。可以看出，在收斂之后，Kalman濾波器能夠很好地從測量電流中把高頻分量提取出來，并且不會造成高頻交流分量的相位滯后和幅值誤差。

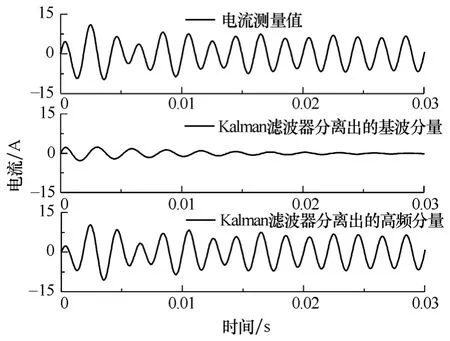
圖3 起動過程中的d軸電流分析結果Fig.3 d-axes current analysis results during startup

6 實驗結果

為了驗證理論分析和仿真結果的有效性，在以TI的C6711浮點DSP和Alter的EP1K100 FPGA為控制器組成的實驗平臺上進行了實驗驗證。電動機為表面貼式永磁同步電動機，電感L=1.25mH。雖然是表面貼式電動機，但是受磁飽和的影響，還會存在一定的凸極效應，因此高頻注入法仍然可以使用。注入高頻信號幅值為 30V，頻率為 500Hz。電動機采用轉子磁場定向矢量控制，d軸電流基頻分量控制為零，控制周期為 100μs。逆變器由 IGBT組成，系統(tǒng)框圖如圖2所示。

電動機從靜止起動到0.5Hz，再加速到10Hz時的機械角速度估計結果如圖4所示，加速過程中轉子位置估計的誤差如圖5所示。可以看出，轉速和轉子位置的估計有很好的穩(wěn)定性和動態(tài)響應速度，角度估計的誤差能控制在一個很小的范圍內。而且該算法不僅可以應用在低速區(qū)域，在高速區(qū)域同樣可以得到很好的性能。在電動機低速空載時，由于電動機的反電動勢和電流都很小，所以噪聲、干擾、測量誤差等的影響就比較明顯，造成低速時轉速控制出現(xiàn)一定的波動。在中高速區(qū)域，轉速和位置估計的精度都能提高。

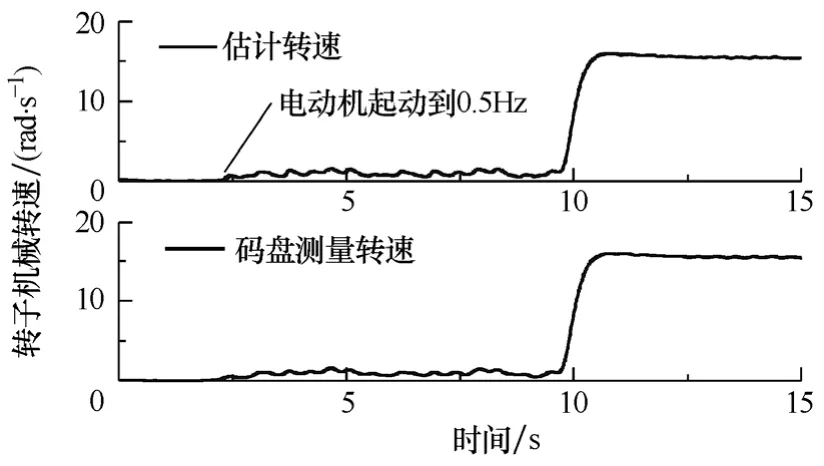
圖4 起動和加速過程中的轉速估計結果Fig.4 Speed estimation results during startup and acceleration

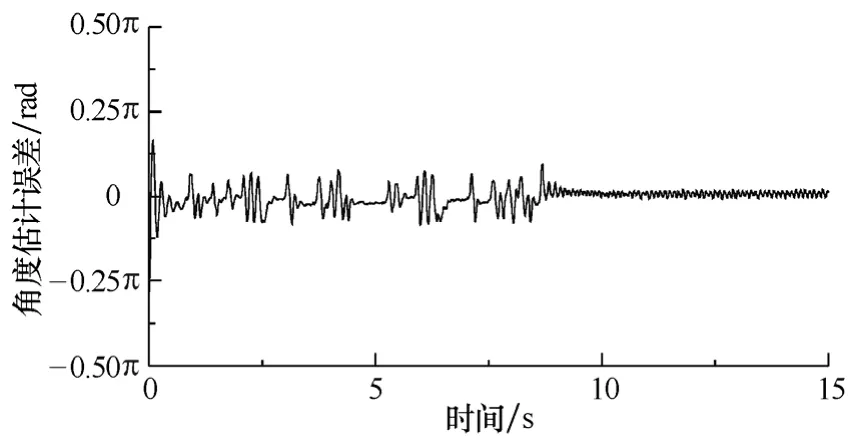
圖5 0.5Hz加速到10Hz時的轉子角度估計誤差Fig.5 Rotor position estimation error during acceleration from 0.5Hz to 10Hz

起動后突加和突減轉矩過程中的轉速估計結果如圖6所示，驗證了系統(tǒng)的帶負載能力。起動過程中，Kalman濾波器（KF）對 d軸電流的信號處理結果如圖7所示，可以看出，Kalman濾波器在很短的時間內就能夠收斂，并準確地分離d軸電流中的高頻分量和基頻分量。

在零速下，對電動機施加一定的轉矩時的轉子轉速波形如圖8所示，可以看出，系統(tǒng)在零速時具有很好的帶負載能力和響應速度，出現(xiàn)負載沖擊之后系統(tǒng)能夠迅速穩(wěn)定。

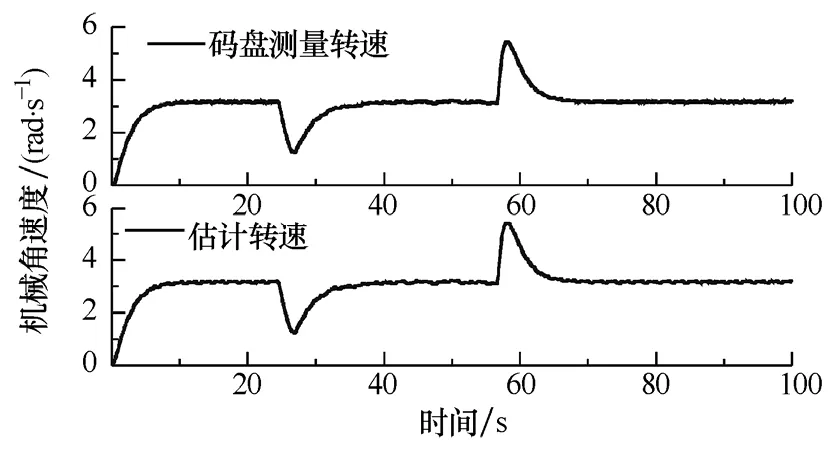
圖6 在負載沖擊過程中的轉速估計結果Fig.6 Speed estimation results during load torque impact

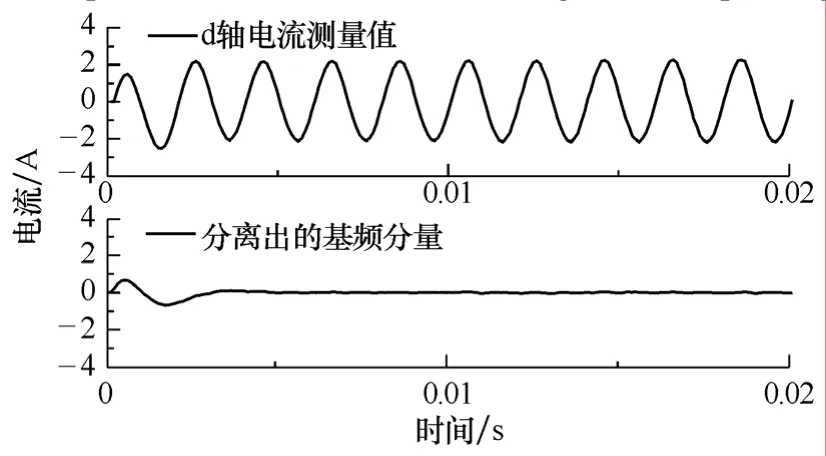
圖7 起動過程中的d軸電流分析結果Fig.7 d-axes current analyses results during startup

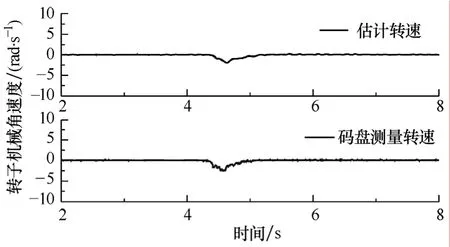
圖8 零速時突加轉矩時的轉子轉速Fig.8 Speed estimation results at zero speed with some load torque impact

7 結論

本文提出了一種利用Kalman濾波器來進行信號處理的高頻信號注入法來估計交流電動機的轉子位置和轉速，提高交流電動機無機械傳感器控制的低速甚至零速控制性能，該方法相比傳統(tǒng)方法，算法簡單直接，系統(tǒng)得到簡化。以永磁同步電動機為例進行的仿真和實驗驗證，表明該方法能夠有效地從測量的電動機電流中提取需要的高頻分量。利用Kalman濾波器的信號處理結果能夠準確估計轉子位置和轉速，是一種非常好的轉子位置和轉速的估計方法，可以實現(xiàn)交流電動機在低速甚至零速下的無機械傳感器控制，并且具有非常好的穩(wěn)定性和動態(tài)響應速度。對于其他的信號注入法如旋轉信號注入法，或者其他類型的電動機如異步電動機等，這種基于 Kalman濾波器的信號處理方法經過簡單修改后同樣適用。

[1] Ji-Hoon J, Jung-Ik H, Ohto M, et al. Analysis of permanent-magnet machine for sensorless control based on high-frequency signal injection[J]. IEEE Trans. on Industry Applications, 2004, 40(6): 1595-1604.

[2] Silva C, Asher G M, Sumner M. Influence of deadtime compensation on rotor position estimation in surface mounted PM machines using HF voltage injection[C]. PCC’02 (Power Conversion Conference),2002, 3: 1279-1284.

[3] 鄭澤東, 李永東, Maurice Fadel, 等. 基于擴展Kalman濾波器的 PMSM 高性能控制系統(tǒng)[J]. 電工技術學報, 2007, 22(10): 18-23.Zheng Z D, Li Y D, Fade1 M, et al. High performance PMSM control system based on extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2007, 22(10): 18-23.

[4] 李劍飛, 尹泉, 萬淑蕓. 基于擴展卡爾曼濾波器的異步電機轉速辨識[J]. 電工技術學報, 2002, 17（5）:40-44.Li Jianfei, Yin Quan, Wan Shuyun. Identify the rotor speed of an asynchronous motor by using the extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2002, 17(5): 40-44.

[5] Choi J W, Sui S K. Inverter output voltage synthesis using novel dead time compensation[J]. IEEE Trans.on Power Electronics, 1996, 11(2): 221-227.

[6] Hide C, Moore T, Smith M. Adaptive Kalman filtering algorithms for integrating GPS and low cost INS[C].PLANS 2004, 2004: 227-233.

[7] Jwo D J, Chang C S, Lin C H. Neural network aided adaptive Kalman filtering for GPS applications[C].ICSMC, 2004, 4: 3686-3691.