運用辯證思維探求解題捷徑

■江思容

運用辯證思維探求解題捷徑

■江思容

所謂辯證思維，就是用運動的、聯系的、對立統一的觀點和方法來思考、研究問題，揭示事物的本質的思維方法。解題是數學學習的基本活動。題目千變萬化，已知和未知之間充滿矛盾的對立統一，在指導學生研究數學問題時，教師要積極引導他們運用聯系轉化觀、對立統一觀、運動變化觀來分析問題、探求問題解決的最佳途徑，這將有利于對學生進行辯證唯物主義教育，提高學生辯證思維能力。本文從以下八個方面談談作法，以期拋磚引玉。

一、一般與特殊

有些數學命題條件與結論之間的聯系，不很明顯，而其結論又是反映一般的情形，直接尋找解題途徑較為困難。在這種情況下，不妨先將問題的一般性轉化為問題的特殊性來考慮。這種探索一般性的結論的方法，有助于我們從特殊性認識普遍性。

例1，方程(m+1)x4-(3m+3)x3-2mx2+18m=0對任何實數m都有一個共同的實數解，試求這個實數解。

解：∵m為任意實數，不妨取m=-1和m=0兩種特殊情形。

(1)將m=-1代入原方程有2x2-18=0，解這個方程得x=±3；

(2)將m=0代入原方程有x4-3x3=0，解這個方程得x=0或3。

而這兩個方程只有公共解x=3，因此方程的實數根是x=3。

二、相等與不等

辯證唯物主義觀點認為，矛盾的雙方是可以互相轉化的，所以我們可用“不等”的方法來解決“相等”的問題，從而讓“不等”向“相等”轉化。

例2，已知a，b，c為整數，且a2+b2+ c2+49≤4a+6b+12c，求的值。

解：∵a、b、c為整數，由已知條件的不等式有：a2+b2+c2+49≤4a+6b+12c。

三、正面與反面

一般來講，從正面解題，是常見的有效的方法，但有時從正面出發思路卻受阻，不知所措，這時若從反面著手常常能化難為易，迎刃而解。

例3，設三個二次方程

x2+4mx+4m2+2m+3=0，

x2+(2m+1)x+m2=0，

(m-1)x2+2mx+m-1=0，

它們中至少有一個方程有實根，則m的取值范圍是（）

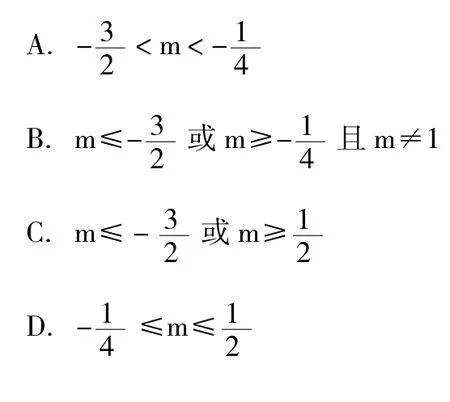
解：此題分以下兩種情況考慮——

(1)當m=1時，方程(m-1)x2+2mx+m -1=0化為一次方程2x=0，它有一個實數根x=0，故m=1符合題意。

(2)當m≠1時，所給方程均為一元二次方程，若從正面考慮，“至少有一個方程有實根”，需分“一個方程有實根”、“兩個方程有實根”、“三個方程有實根”一一進行討論，共需列七個不等式(組)，運算相當繁雜。若轉化到問題的反面，先求三個二次方程都無實根時m的取值范圍，然后從m≠1的實數中排除它即為所求。

且m≠1，故選(B)

四、運動與靜止

當題目中變量較多或不確定因素較多時，全面考慮難度較大，為此可“動”中求“靜”，而有時，要反其道而行之。

例4，如圖1，邊長為a的等邊△ABC的二頂點A、B，分別在x軸和y軸上運動，試求動點C到原點O的距離的最大值和最小值。

解析：由于求動點C到原點O的距離的最大值比較困難，根據相對運動原理，可以考慮把定點O轉化為動點，把動點C轉化為定點，讓坐標軸運動，由于∠xOy=90°，原點O就在以AB為直徑的圓上運動，當AO=BO時，CO最大，CE最小。

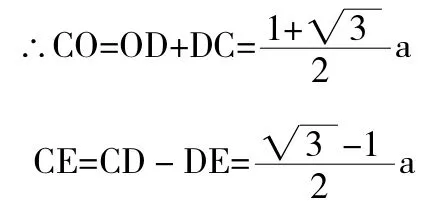
五、熟悉與陌生

熟悉與陌生是一對矛盾，把比較生疏的問題轉化為熟悉的問題，以充分利用已有的知識和經驗，使問題得以解決，這是解題化歸思想中一個重要原則。

例5，若(b-c)2-4(a-b)(c-a)=0，求證：2a=b+c

證明：∵條件等式類似于一元二次方程判別式，于是可構造熟悉的一元二次方程即(a-b)x2+(b-c)x+(c-a)=0，

∵(a-b)+(b-c)+(c-a)=0及△=0知x1=x2=1，

六、隱含與明顯

在數學解題中，常把題中的隱含條件轉化為顯現的條件，增加問題的透明度。

解析：本題若直接代換計算，則相當麻煩，仔細觀察，不難發現其隱含條件是x-y=1，這樣就增加了問題的透明度。

于是，原式=(x-y)(x2+xy+y2)-3xy= (x-y)2=1

七、無限與有限

數學中涉及無限多情形的問題，常因難以統一處理而成難題，但有些可通過適當處理，轉化為有限的問題來解決。

例7．求證：等式

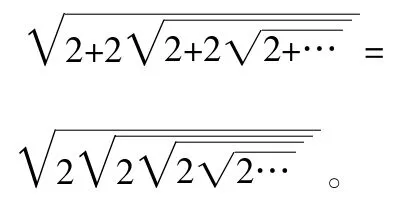
證明：設左邊=x，兩邊平方后有2+2x=x2，解之得x1=2，x2=-1(不合題意舍去)，再設右邊=y，兩邊平方后有2y=y2，解之得y1=2，y2=0(舍去)

∴x=y=2。

故原命題成立。

八、前進與后退

解決一個特殊數學問題時，往往可先將這個問題作一般化的探討，推進到一般的情形，通過對一般問題的解決，再返回來解決原來的問題，以達到最終解決問題的目的。

例8，如圖2，AD是△ABC的中線，AD上一點E，過E的直線交AB于 F、AC于G。求證：。

綜上所述，引導學生用辯證的觀點去觀察問題、解決問題，努力促進學生掌握辯證思維這個銳利武器，將能大大提高學生的思維能力和解題能力。

武漢市洪山區教育研究培訓中心）

責任編輯 王愛民