提高超窄橋面加勁梁懸索橋顫振穩定的措施研究

尹建芳

(河北省第四建筑工程公司，石家莊 050011)

1 橋梁概況

劉家峽大橋為主跨536 m的單跨桁架式加勁梁懸索橋，主纜跨度布置為(150+536+115)m，垂跨比為1/11，總體布置如圖1所示。主纜采用預制平行鋼絲束股，兩根主纜的中心間距為15.6 m，每根主纜由44束127根φ5.2 mm高強鍍鋅鋼絲組成，鍍鋅鋼絲極限抗拉強度為1 670 MPa。吊索由73根 φ5.0 mm高強鍍鋅鋼絲組成，吊索縱橋向標準間距為8 m。主塔采用鋼管混凝土門形框架結構，兩岸塔高均為67.0 m，錨碇采用三角框架式重力錨。主桁采用型鋼桁架，桁高4.0 m，節間長4.0 m，兩片主桁間距與主纜間距相同。橋面系由正交異性鋼橋面板、縱梁、U肋和橫隔梁組成，其中，橋面板厚度為16 mm。

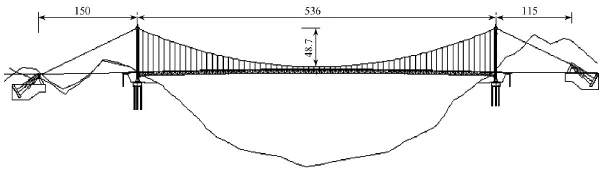
圖1 橋梁總體布置(單位:m)

劉家峽大橋位于二級公路，受建設條件制約，橋面寬度僅15.6 m，在國內同規模橋梁中最窄，主纜重力剛度低，抗風問題較為突出。根據劉家峽大橋風洞試驗結果，若不采取任何抗風措施的情況下，顫振臨界風速遠低于顫振檢驗風速，抗風穩定不滿足要求。為此，需要采取合理措施解決劉家峽大橋抗風穩定問題。本文從結構措施和氣動措施兩方面入手，研究劉家峽大橋抗風方案。首先通過套用古典耦合顫振理論來研究結構措施，然后通過風洞試驗手段研究氣動措施。

2 關于顫振穩定的分析方法

近地風是一種紊流風。劉家峽大橋采用桁架式加勁梁，而并非采用流線型截面形式的加勁梁。紊流風場對于振動著的非流線型截面所產生的非定常空氣力無法用解析形式表達出來，只能用風洞試驗的途徑來確定。但為了研究影響抗風穩定的主要因素并優化參數，本文分析仍套用適用于流線型截面的古典耦合顫振檢算公式。其研究結果仍然可以在一定程度上反映劉家峽大橋的抗風顫振穩定問題。

1935年，Theodorson首先從理論上研究了薄平板的空氣作用力，用勢能理論求得了作用于振動平板上的非定常空氣力的解析表達式。1976年，VanderPut提出了平板顫振臨界風速Vcr的簡化計算公式

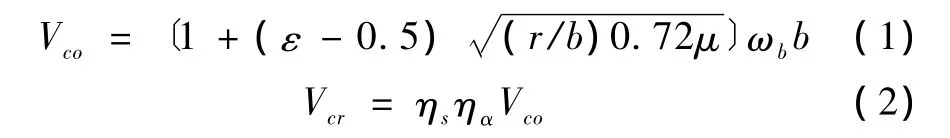
式中，Vco為臨界風速(m/s);ε 為扭彎頻比，ε = ωt/ωb，ωb為抗彎基頻，ωt為抗扭基頻;μ為橋面質量與空氣的密度比，μ =m/(πρb2)，ρ=0.125 kg/m3，m 為橋面每延米的質量;r/b為橋面慣性半徑比，r/b=為橋面每延米質量慣性矩(kg·m2/m)，m′為加勁梁半寬(m);ηs，ηα為形狀系數，ηs=0.7，ηα=0.8。

從式(1)可以分析出，豎向彎曲頻率對結構顫振穩定具有不利影響。扭轉基頻可以顯著提高顫振臨界風速，對顫振穩定起有利作用。豎彎基頻可降低臨界風速，對顫振穩定起不利作用。為了改善劉家峽大橋顫振穩定性，則需要提高結構的扭轉基頻或降低豎彎基頻。

3 提高顫振穩定的結構性措施研究

3.1 優化纜索體系

主纜對全橋剛度貢獻主要反映在主纜線形(即主纜垂跨比)和主纜拉力大小上。為此，針對以上因素進行研究，圖2給出了振動基頻隨主纜垂跨比變化曲線，圖3給出了振動基頻隨主纜拉力變化曲線。

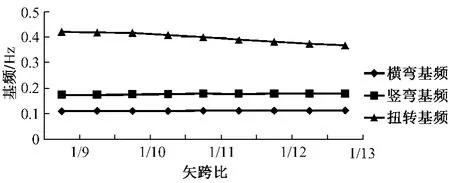
圖2 基頻隨主纜垂跨比變化曲線

從圖2可見，扭轉基頻隨垂跨比的減小而減小;橫彎基頻和豎彎基頻隨垂跨比保持不變。當垂跨比由1/9變化到1/13時，扭轉基頻降低12.6%。

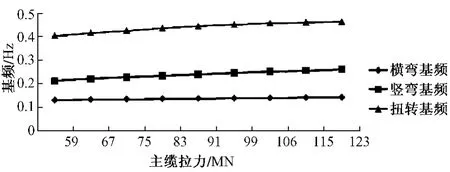
圖3 基頻隨主纜拉力變化曲線

從圖3可見，扭轉、橫彎和豎彎基頻均隨主纜拉力增加而增加，當主纜拉力增加1倍時，豎彎基頻可增加23%，橫彎基頻可提高 9.2%，扭轉基頻可增加14.5%。

綜上，若提高臨界風速，應提高扭轉基頻或降低豎彎基頻，即需降低垂跨比或提高主纜拉力。隨著垂跨比的降低，主纜拉力將隨之提高，扭轉基頻也會提高，但豎彎基頻也會隨著提高，對臨界風速具有一定折減作用。經分析，若采用提高垂跨比、增加主纜拉力的方案來提高臨界風速，效果并不明顯，而且會引起活載應力比例提高，豎彎剛度下降，對行車舒適性也有不利影響。

3.2 改變梁高

為了研究加勁梁高度對典型自振基頻的影響，將梁高由1 m變化到10 m，主纜垂跨比取1/11。考慮梁高變化引起質量、主纜拉力變化影響，主纜應力保持不變。圖4給出了臨界風速提高百分比與梁高變化的關系。隨著梁高的增加，主纜拉力和加勁梁弦桿軸力均隨之增加，主纜和加勁梁用鋼量也必然增加。為了綜合反映橋梁用鋼量變化，根據主纜和加勁梁的造價比，引入了加權用鋼量變量，以直接反映橋梁造價的變化。圖5給出了換算用鋼量變化百分比隨梁高變化曲線。

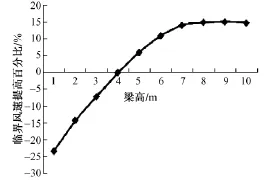
圖4 臨界風速隨梁高變化關系

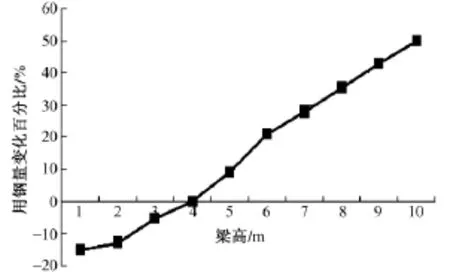
圖5 換算用鋼量隨梁高變化關系

從圖4和圖5可見，隨著梁高的增加，臨界風速隨之提高，但當梁高增加到7 m時，顫振臨界風速趨于穩定，僅提高約15%，而此時用鋼量已增加30%。由此可見，通過增加梁高來提高結構顫振穩定性可能會帶來整體造價的大幅度提高，若梁高超過7 m后，則不應繼續增加梁高。

3.3 改變梁寬

為了研究加勁梁梁寬對典型自振基頻的影響，梁寬由12 m變化到24 m，主纜垂跨比取1/11，考慮梁高變化引起質量、主纜拉力變化影響，主纜應力保持不變。圖6給出了臨界風速提高百分比與梁寬變化的關系。隨著梁寬的增加，主纜拉力、橫梁受力隨之加大，主桁弦桿軸力均基本不變，然而，主纜、加勁梁、橋面用鋼量必然增加。根據主纜和加勁梁的造價比，引入了加權用鋼量變量，以直接反映橋梁造價的變化。圖7給出了換算用鋼量變化百分比隨梁寬變化曲線。

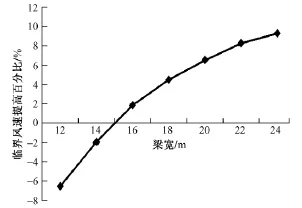
圖6 臨界風速隨梁寬變化關系

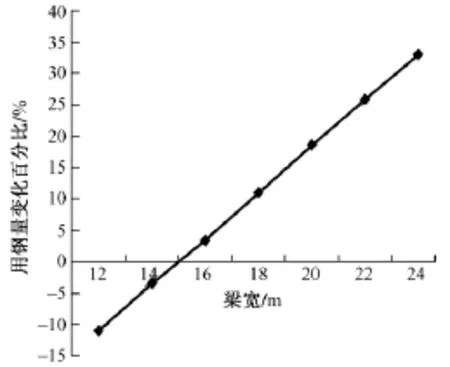
圖7 換算用鋼量隨梁寬變化關系

從圖6、圖7可見，以15.6 m為基準，梁寬增加至24 m后，臨界風速可提高9.34%，但用鋼量卻增加33%。由此可見，通過增加梁寬來提高結構顫振穩定性可能會帶來整體造價的大幅度提高，若僅僅通過加大梁寬來提高臨界風速是不經濟的。

3.4 設置抗風纜

通過架設抗風纜可以提高橋梁的顫振穩定，國內很多小跨度懸索橋均采用此方案。但由于架設風纜會影響到橋梁美觀且施工難度較大，目前國內大跨度懸索橋尚無采用的先例。抗風纜的形式分為三種:平行式、外張式和內收式，如圖8所示。

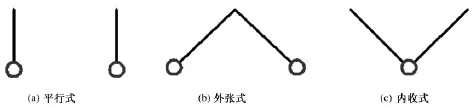
圖8 抗風纜布置的三種形式

為了便于比較，將三種風纜形式的風纜張力均按30%主纜力施加，垂跨比均取1/30，研究三種方案對顫振穩定的影響。表1給出了各方案典型振動頻率的提高百分比。從表1可見，三種方案豎向彎曲基頻提高幅度均較大，扭轉基頻提高幅度均較小。外張式方案對橫向彎曲提高幅度最大，最大可提高40.2%。平行式方案對豎向彎曲提高幅度最大，最大可提高40.3%。平行式方案對扭轉基頻提高幅度最大，最大可提高12.5%。

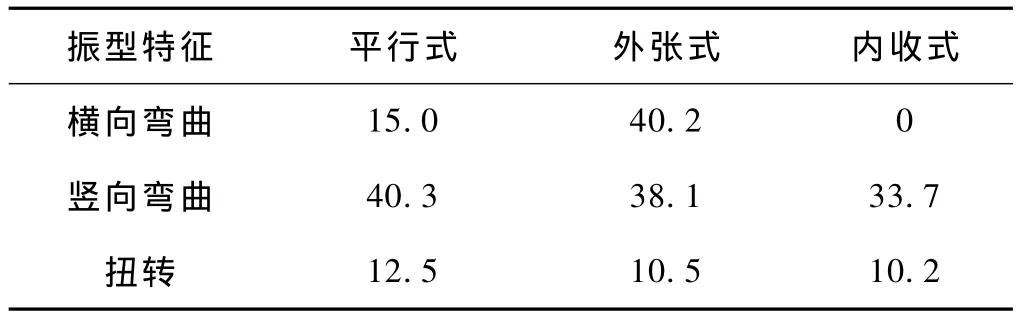
表1 各方案典型振動頻率提高百分比 %

根據有限元分析結果，采用風纜扭轉基頻可有一定的提高，但豎彎基頻提高幅度較大，對顫振臨界風速有一定的折減作用。各方案中，平行式風纜臨界風速提高幅度最大，但也僅提高約7%。然而，由于增加抗風纜，顫振臨界風速還會受到風纜恢復力的影響，風纜對升力、扭轉有一定的抵抗作用，應可增加顫振臨界風速。一些簡易橋的風纜，沒有初張力，橋面基本沒有扭轉剛度，風纜也沒有提高扭轉基頻，但事實表明風纜很有效。可見，采用二維理論計算中頻率的簡單函數解釋增加風纜后懸索橋的顫振已不適宜，從理論上對風纜恢復力對顫振臨界風速影響進行分析存在困難，也應通過風洞試驗確定。在實際工程中，大跨懸索橋采用風纜存在施工不便的不利條件，且施加初張力后，還會引起主纜纜力的增加，繼而影響橋塔、錨碇工程量的增加。

4 提高顫振穩定的氣動措施研究

根據前面的分析，若僅通過結構措施來解決劉家峽大橋抗風不足問題，可能會造成橋梁造價大幅度提高。為了得到更合理的抗風方案，本文通過風洞試驗來研究提高顫振穩定的氣動措施。試驗在均勻流場中進行，采用直接試驗法對成橋狀態進行了-3°、0°和3°三種攻角的豎彎和扭轉兩自由度耦合顫振試驗。

4.1 設置下穩定板

首先提出了在桁架內部設置下中央穩定板的方案，下中央穩定板高度取1.12 m，風洞實驗結果見表2所示。由表2可知，該方案 0°和 +3°攻角條件下，顫振臨界風速小于顫振檢驗風速［Vcr］=62.6 m/s，說明結構顫振穩定不滿足要求。

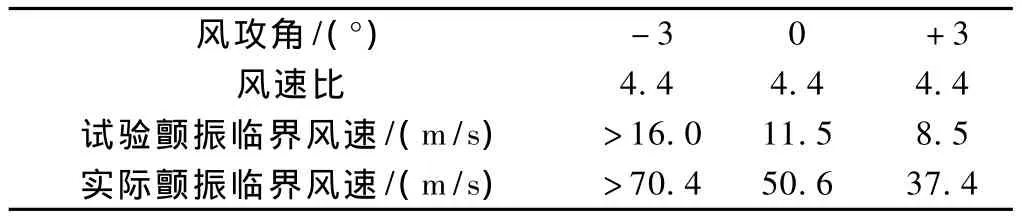
表2 設置下中央穩定板時顫振臨界風速值

4.2 設置上穩定板和下穩定板

通過分析提出了第二種氣動措施，在桁架內部設置上、下中央穩定板。上穩定板高度取1.28 m，下穩定板高度取1.12 m，風洞試驗結果見表3所示。由表3可知，該方案三種攻角條件下，顫振臨界風速均大于顫振檢驗風速［Vcr］=62.6 m/s，說明結構顫振穩定可滿足要求，并留有足夠的富裕。

表3 設置上、下中央穩定板時顫振臨界風速值

4.3 設置下穩定板和水平導流板

由于劉家峽大橋位于二級公路上，橋面寬度較小，不便設中央分隔帶，設上穩定板并不合理。為此，提出了第三種氣動措施，即采取設下中央穩定板(板高h=1.28 m)、水平導流板(板長 L=2 m)以及封閉部分防撞欄的抗風方案，風洞試驗結果如表4所示。由表4可知，該方案三種攻角條件下，顫振臨界風速均大于顫振檢驗風速［Vcr］=62.6 m/s，說明結構顫振穩定可滿足要求。試驗也表明本橋無明顯渦振現象。

表4 設置下穩定板和水平導流板時顫振臨界風速值

5 結論

劉家峽大橋橋面寬度在國內同規模橋梁中最窄，主纜重力剛度低，對于橋面較窄的桁式加勁梁懸索橋，抗風問題較為突出，本文從結構措施和氣動措施兩方面分別研究了劉家峽大橋顫振穩定問題。

主纜線形和應力水平、加勁梁梁高和梁寬以及張拉風纜都會影響橋梁臨界風速，但效果并不理想。通過引入用鋼量經濟性指標進行優化計算后發現，若僅通過結構措施解決超窄橋面桁式加勁梁懸索橋的抗風顫振穩定問題是不經濟的，應結合氣動措施進行抗風方案優化。本文提出了三種氣動措施。根據風洞試驗結果，僅設置下穩定板方案并不能解決抗風穩定問題。若同時設置上、下穩定板方案可以解決抗風穩定不足的問題，但由于劉家峽大橋位于二級公路上，設置上穩定板并不合理。第三種方案是同時設置下穩定板和水平導流板，風洞試驗結果表明，該方案各種工況下顫振臨界風速均大于顫振檢驗風速，說明結構顫振穩定可滿足要求，試驗也表明本橋無明顯渦振現象。綜上，認為同時設置下穩定板和水平導流板是解決超窄橋面懸索橋抗風穩定不足的合理氣動措施。

本文研究結果表明，若想解決超窄橋面加勁梁懸索橋的抗風穩定問題，應從結構措施和氣動措施兩方面研究入手。首先，要確定合理的結構形式，然后，在此基礎上進行氣動措施研究。這樣，才能得到合理的抗風方案。

［1］ZHANG Xinjun，SUN Bingnan，XIANG Haifan.Nonliear Aerostatic and Aerodynamic Analysis of Long-span Sunpension Bridges Considering Wind-structure Interactions［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90(9):1065-1080.

［2］陳艾榮，宋錦忠.鎮江揚州長江大橋抗風性能研究報告［R］.上海:同濟大學土木工程防災國家重點實驗室，2000.

［3］李國豪.橋梁結構穩定與振動［M］.北京:中國鐵道出版社，2003.

［4］華旭剛，陳政清.一種基于 ANSYS的顫振頻域分析方法［C］∥第12屆全國結構風工程會議.西安:長安大學，2005:517-525.

［5］AGAR T J A.Aerodynamic flutter analysis of suspension bridges by a modal technique［J］.Engineering Structure，1989，11(2):75-82.

［6］祝志文，汪志昊，陳政清.三汊磯大橋顫振穩定性的風洞試驗與研究［J］.中南公路工程，2006，31(4):19-23.