雙螺桿泵流場動力特性的數值模擬

唐 倩 張元勛 高 瞻

1.重慶大學機械傳動國家重點實驗室,重慶,400044 2.重慶中冶賽迪工程技術股份有限公司,重慶,400013

0 引言

雙螺桿泵以其節能環保、平穩可靠等優點,廣泛應用于石油、環保等支柱產業。目前所有對螺桿泵螺桿傳動系統的研究均是圍繞螺桿轉子型線的修正和轉子力學性能展開的,而對于螺桿內部流場的流道特性、系統的動態特性等關鍵技術的研究還未見報道。泵內流體的流動狀態具有復雜、非定常、不可壓縮、黏性等特性,直接影響螺桿泵的性能,由于雙螺桿泵幾何結構及流動特性復雜,很難采用數學解析求解,因而如采用試驗方法來驗證幾何設計的合理性,會耗費大量的人力和資金[1-7]。

本文以自主設計的漸開線修形雙螺桿泵為研究對象,基于有限容積法,對螺桿泵內部流場的速度、壓力進行流體動力學分析,得出雙螺桿泵內部流場主要特征和分布規律,進而研究其結構改進及性能改善的方法,為雙螺桿泵的設計提供理論依據。

1 雙螺桿泵結構設計及仿真模型

1.1 螺桿的結構設計

由雙螺桿泵工作原理知,相互嚙合的兩根螺桿的嚙合線將螺旋槽分割成互不相通的腔體,其齒廓曲線一般采用外長擺線;而僅有外長擺線時,齒頂處的夾角小于90o,齒頂處的螺旋線與主螺桿的螺旋面相嚙合,主要起密封作用,因此齒頂的銳角在主螺桿、從螺桿相互嚙合傳遞力矩時必然會很快磨損,從而破壞螺桿泵的密封性[8-9]。為了增強從螺桿齒頂的耐磨能力,本文應用漸開線對螺桿的齒廓曲線進行修正,根據包絡的定義推導出主螺桿的修正曲線(以下簡稱漸開線修形)。圖1中,Ⅰ為主螺桿修形前后對比圖,Ⅱ為從螺桿修形前后對比圖。從圖中可以看出,修形后從螺桿齒頂與主桿相嚙合的點轉化為漸開線段,使得齒廓間的嚙合由點-線嚙合轉化為線-線嚙合,從而形成連續的嚙合線,增強了密封性,提高了泵的容積效率。

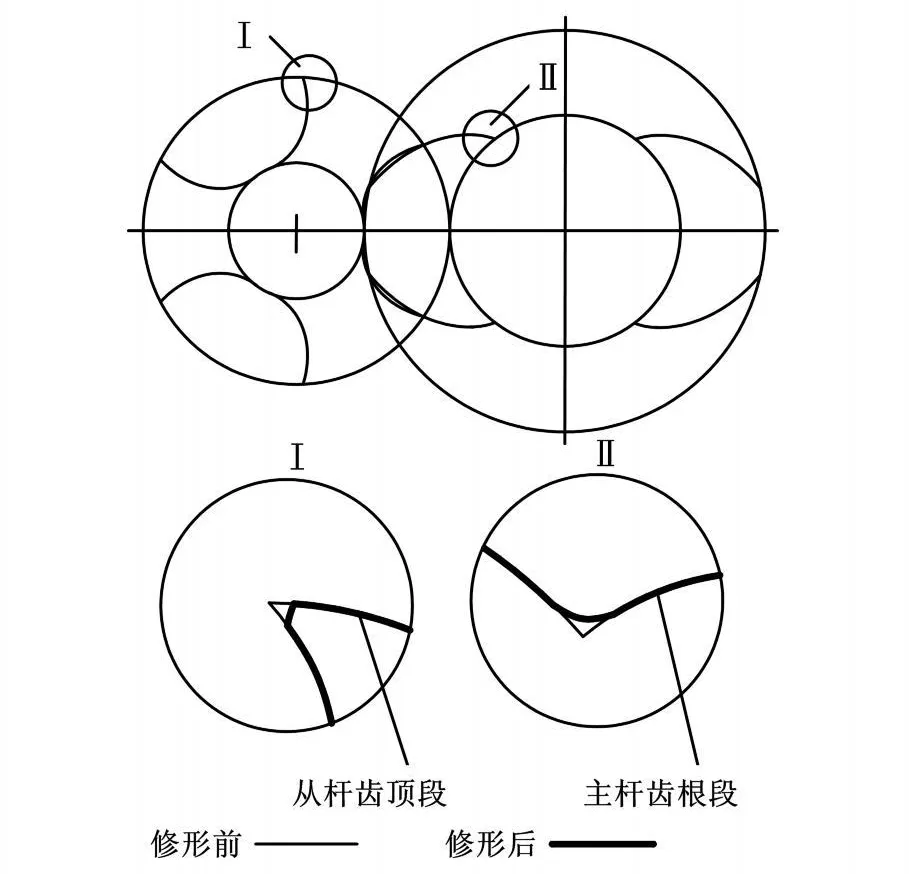
圖1 螺桿端面齒形曲線示意圖

1.2 三維實體及網格模型

根據所設計的螺桿幾何參數(表1)以及修形后的端面齒廓,采用Pro/ENGINEER三維造型軟件建立了雙螺桿泵三維流道幾何模型,將其導入網格劃分軟件ANSA以對整個流道進行四面體網格劃分,其中擺線型雙螺桿泵(圖 2)網格總數755 390,節點總數154 842,單元網格最小體積3.1276×10-12mm3,最大體積3.352 893×10-12mm3;漸開線修形雙螺桿泵(圖 3)網格總數830 659,節點總數173 921,單元網格最小體積1.0312×10-12mm3,最大體積2.7784×10-8mm3。

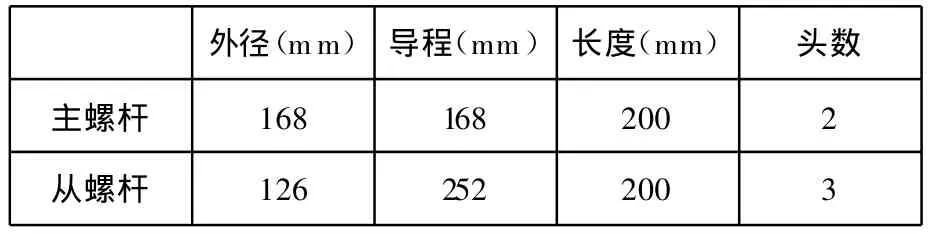
表1 主從螺桿幾何參數

圖2 擺線型雙螺桿泵流道網格圖

圖3 漸開線修形雙螺桿泵流道網格模型

2 雙螺桿泵湍流模型

2.1 湍流模型

雙螺桿泵流場流動為復雜的湍流問題,采用基于Reynolds時均方程的模擬方法來建立湍流模型。雙螺桿泵的湍流是指由于壓差、各流速層之間的流速差以及工作容積、空間形狀隨螺桿的運轉而改變等因素造成的液體在各方向和流速上的紊亂流動。本文針對雙螺桿泵流道液體流動問題,采用標準k-ε雙方程模型進行分析。

2.2 邊界條件

為擬定流場,考慮到流體的輸送具體條件及流場特性,作以下假設：①流體為不可壓縮、牛頓流體;②流場為穩定、等溫流場;③慣性力、重力等體積力遠小于黏滯力,可忽略不計;④流體在流道中完全充滿。

在雙螺桿泵流道流場模擬計算過程中,主要涉及的邊界分別為：入口端面,出口端面,左右螺桿外表面,機筒內表面。泵流場內部液體為潤滑油液CD40。入口壓力50kPa,出口壓力0.8MPa。

在確定雙螺桿泵流道流動邊界時,一個主要難點是：當螺桿轉動時,流動邊界是隨時間變化的。這種隨時間變化的流動邊界問題一般是通過用一系列不同相位的瞬時流場模型代表一個完整時間周期的模型來解決的[10-12]。在螺桿旋轉一周的時間里,按等時間間隔均勻取出不同瞬時的流場模型來代表整個流場模型。考慮螺桿的對稱性,流道在螺桿旋轉時的前180°模型邊界同后180°的模型邊界是一一對應的,因此,間隔30°取出其中的6個瞬時模型即可代表整個隨時間變化的流動邊界。

初始相位角θ定義為螺桿流道前端面上主螺桿中心線與X軸的夾角,為了考察初始相位角對流場特性的影響,即對流量、回流量及加權剪切應力的影響,本文選取了漸開線修形雙螺桿泵流道的6個不同初始相位角時的流場模型。

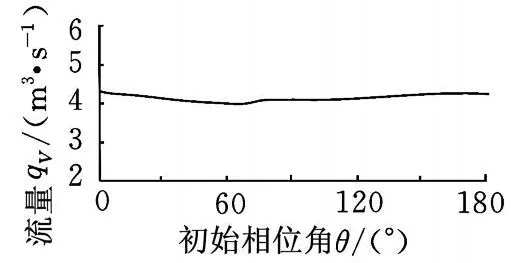
圖4 θ與流量關系

對上述不同初始相位角下的6個流場模型分別進行計算,得到初始相位角 θ與流量、回流量及加權剪切應力的影響,結果如圖4～圖 6所示。由圖4～圖6可以看出,隨著雙螺桿泵流道初始相位角的變化,流量、回流量的變化很小,而剪切應力則沒有變化,說明初始相位角對流場的影響不大,因此,采用某一瞬時的流場模型來代表按時間周期變化的雙螺桿泵流場的方法是可行的。本文采用0°初始相位角的流場模型來進行計算。

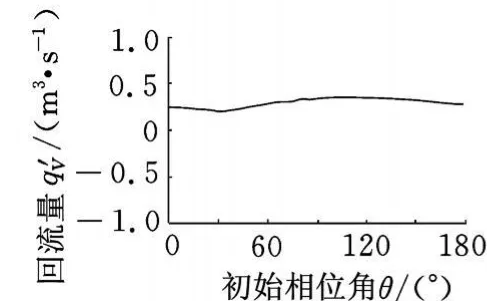
圖5 θ與回流量關系

圖6 θ與加權剪切應力關系

3 雙螺桿泵數值仿真分析

采用流體專用分析軟件Fluent對螺桿泵內部流場進行仿真分析。壓力速度耦合采用SIMPLIC算法,并監測進出口流量變化,當進出口流量變化趨向穩定時說明計算結果收斂。

對整個內部流動區域取合適的截面,以獲得需要的計算結果并進行詳細分析。圖7、圖8是雙螺桿泵流道對稱面壓力分布云圖,可以看出,對稱截面流道內存在四級壓力梯度,且壓力從入口的低壓逐級增大,到出口處達到0.8MPa左右,主從螺桿嚙合區高低壓交替變化。

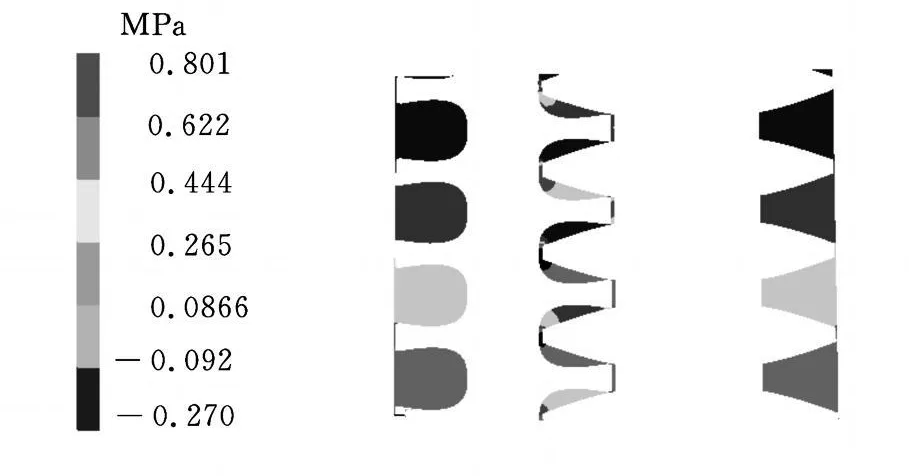
圖7 擺線雙螺桿泵流道對稱面壓力圖

為了更清晰地分析流道內壓力p沿軸向的分布情況,分別取漸開線修形雙螺桿泵主螺桿A1、A2點(圖 9),從螺桿 B1、B2、B3點(圖 9)的壓力值沿螺旋流線方向展開,得到其壓力隨軸向位置的變化圖(圖10、圖11)。

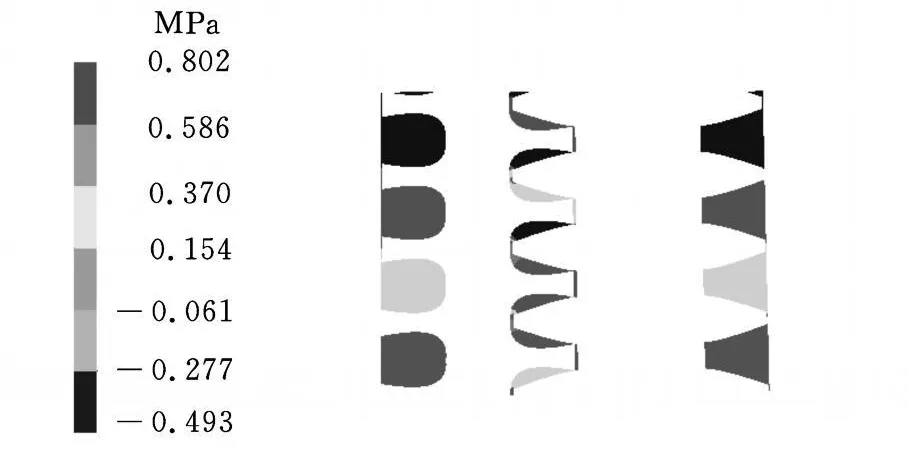
圖8 漸開線修形雙螺桿泵流道對稱面壓力圖

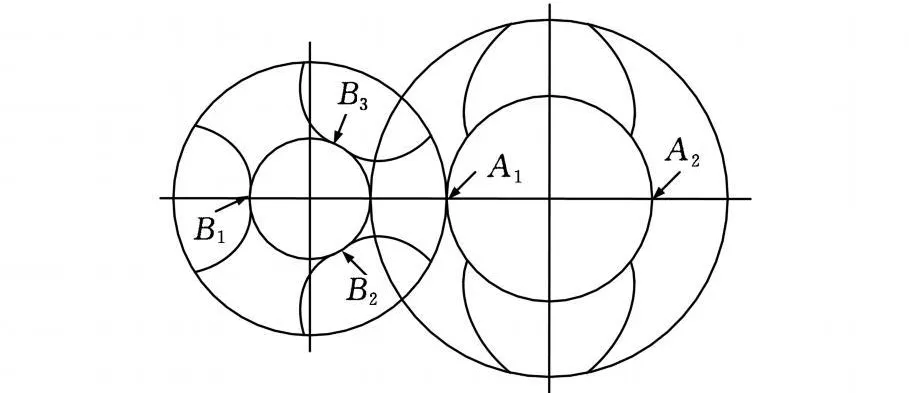
圖9 螺桿機筒關系圖

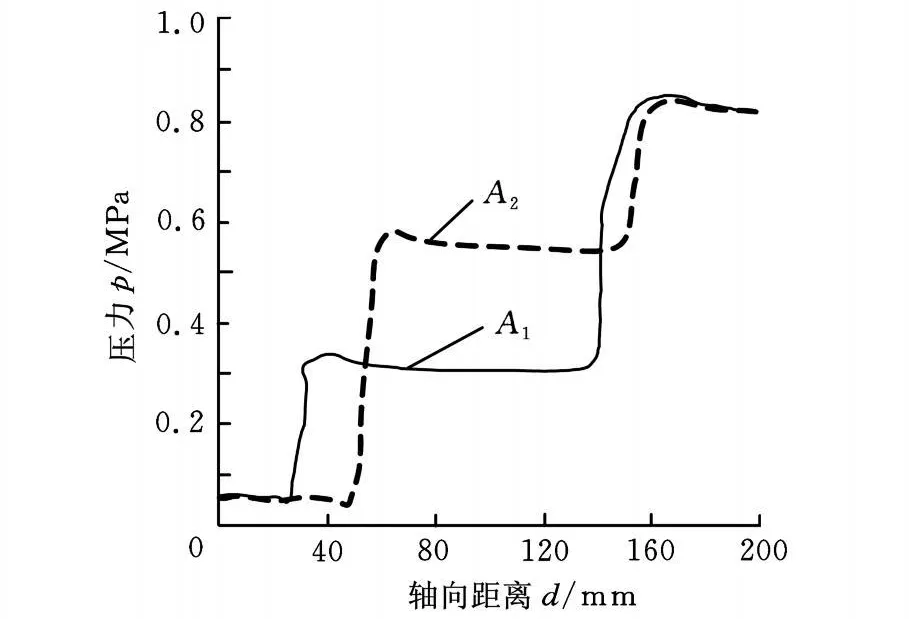
圖10 主螺桿壓力趨勢圖

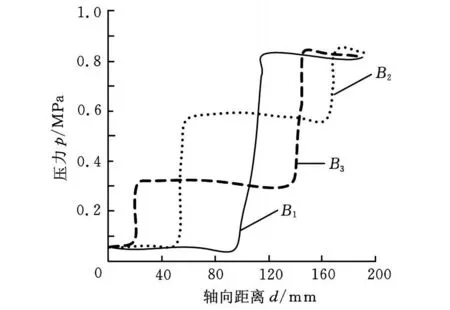
圖11 從螺桿壓力趨勢圖

由圖7和圖8可知,擺線雙螺桿泵與漸開線修形雙螺桿泵壓力分布趨勢相似。由圖10、圖11可知,雙螺桿泵在工作時,液體壓力從低壓腔到高壓腔是階梯變化的,壓力是隨著密封腔而逐級增大的,但同一級內由于泄漏的原因,在該級壓力范圍內沿軸向逐漸減小。

圖12、圖13為流道在軸向50mm處截面的速度矢量圖,由圖能直觀地觀察到液體在此截面處的運動狀態,可以看出,液體在螺槽內的運動是復雜的湍流流動,液體在螺桿的拖拽帶動下,總體沿圓周方向運動。螺槽區域內液體的運動十分復雜,從截面速度矢量圖可以明顯看出螺槽區的渦流流動,液體在螺槽Ⅰ、Ⅱ、Ⅲ處易產生渦流,此三個螺槽靠近嚙合區,受液體經過嚙合區時速度矢量發生突變的影響較大,原來較為規則的圓周運動軌跡將被破壞。

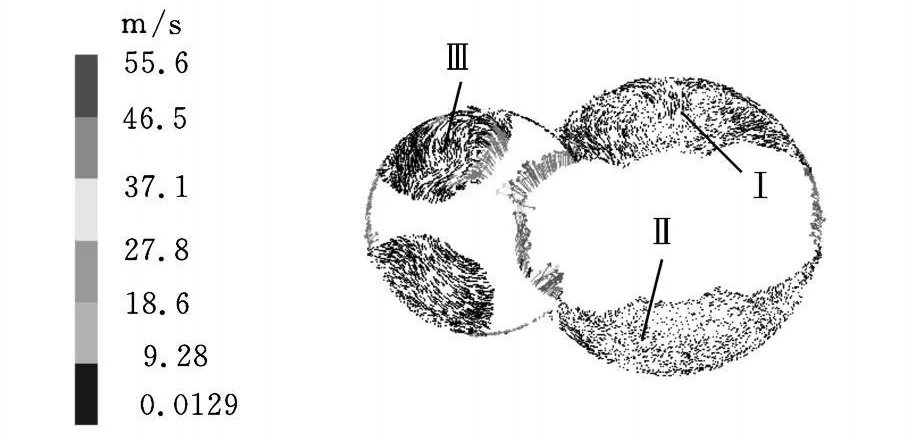
圖12 擺線雙螺桿泵軸向50mm處截面速度矢量圖

圖13 漸開線修形雙螺桿泵軸向50mm處截面速度矢量圖

圖14 ～圖16為流道軸向50mm處截面的軸向速度分布圖,可以看出,在螺桿壁面區域為正速度,且速度相對其他區域較大,說明此處受正向剪切作用的影響,流體是沿泵出口擠出的,不存在回流現象;螺槽區及嚙合區速度分布較復雜,既有正速度又有負速度;螺槽與泵套間間隙處為負速度區域,螺槽區渦流中心及嚙合區速度交換處是負速度最大區域,說明泄漏主要存在于流道間隙處、流體渦流中心及嚙合區。由圖14～圖16可知,漸開線修形雙螺桿泵流場與擺線雙螺桿泵流場軸向速度分布趨勢相同,但漸開線修形雙螺桿泵流道平均速度場大于擺線雙螺桿泵流道速度場,說明漸開線修形雙螺桿泵輸送能力強于擺線雙螺桿泵。

容積損失是雙螺桿泵流道的主要損失形式之一,因為嚙合螺桿之間、螺桿與泵套間存在間隙,而液體受軸向壓力梯度和切向壓力梯度的作用,在這些間隙中產生流動,其中一些流動方向與流出方向相反,形成回流。不同結構的螺桿元件組成的流道幾何結構不同,因此具有不同的回流量。通過整個流道正負速度的積分計算,得到雙螺桿泵流道的流量,進而得出雙螺桿泵容積效率(圖17)。由圖17可知,漸開線修形雙螺桿泵流道的輸送能力較為優越。

圖14 擺線雙螺桿泵軸向50mm處截面速度圖

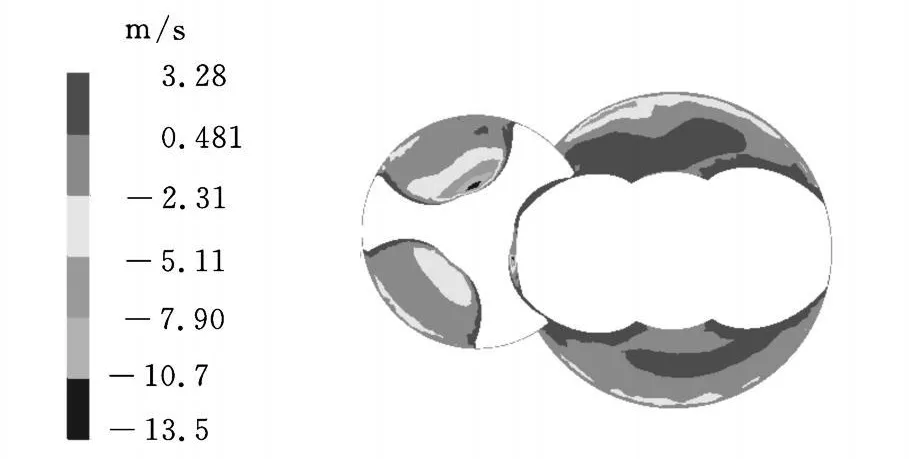
圖15 漸開線修形雙螺桿泵軸向50mm處截面速度圖

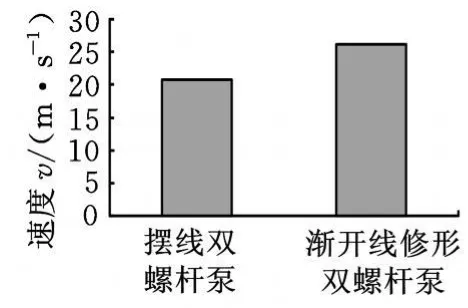
圖16 兩種流道平均加權速度圖

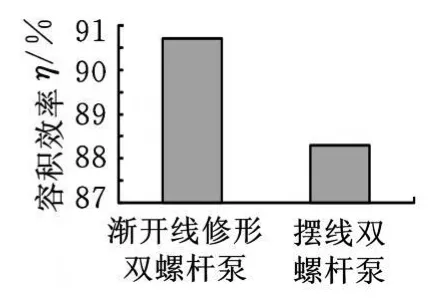
圖17 兩種流道容積效率比較圖

4 結論

(1)轉子嚙合區壓力變化梯度大、剪切應力大,混合擠壓能力強。

(2)主要回流區域為流道間隙處、流體渦流中心及嚙合區。

(3)漸開線修形雙螺桿泵回流量相對較小,容積效率較高,密閉性能更優越,輸送能力更強。

[1] 張洪森,趙煒,李發榮.螺桿泵應用發展14年[J].國外油田工程,2004,20(5)：21-23.

[2] 張寒峭.螺桿泵及新型組件的新進展[J].石油機械,2005,33(11)：81-82.

[3] 陳金海,王麗霞,陳德偉.雙螺桿泵型線的修正[J].流體機械,2006,34(6)：41-43.

[4] Tone S H,Yang D CH.Rotor Profiles Synthesis for Lobe Pumps with Given Flow Rate Functions[J].ASME Journal of Mechanical Design,2005(2)：287-294.

[5] Ryazantsev V M.Radial Forces and Screw Rigidity in a Two-screw Multiphase Pump[J].Chemical and Petroleum Engineering,2001,37(11/12)：617-622.

[6] 王福軍.計算流體動力學分析——CFD軟件原理與應用[M].北京：清華大學出版社,2004.

[7] 劉峰,朱向哲.雙螺桿擠出機齒型螺紋元件三維流場分析[J].石油化工設備,2008,37(3)：37-39.

[8] 于鳳榮,閆國軍,張建蓉.射流泵流場三維數值模擬[J].水泵技術,2006(6)：21-23.

[9] 蔣炎坤,鐘毅芳,周濟,等.基于流場動力學行為的機械產品結構性能研究[J].機械工程學報,2002,38(4)：115-119.

[10] 荊珂.雙螺桿反應器組合螺桿的三維流場數值模擬[J].機械設計與制造,2008(5)：85-87.

[11] Berand F,Tanguy P A,Thibault F.A Threedimension Fictitious Domain Method for Incompressible Fluid Flow Problems[J].International Journal for Numerical Methods in Fluids,1997,25(6)：719-736.

[12] Cao Feng,Peng Yueyuan,Xin Ziwen,et al.Thermodynamic Performance Simulation of a Twinscrew Multiphase Pump[J].Proceedings of the Institution of Mechanical Engineers,2001,215(2)：157-163.