基于二階矩約束的最大熵先驗信息解及其在數控系統可靠性評估中的應用
凌 光 戴 怡 李 曦
1.天津工程師范學院,天津,300222 2.華中科技大學,武漢,430074
0 引言
Bayes方法是解決小子樣問題的一個重要方法,其核心和關鍵是如何利用先驗信息確定先驗分布。根據早期研究,數控系統失效時間服從雙參數Weibull分布。目前,雙參數先驗分布的確定未能得到很好解決:基于1/(θβ)形式的假設的方法[1]雖然簡化了雙參數相互間的關系,但在一定程度上影響了該方法的精度;獨立參數分布的截尾Γ分布和截尾Γ-1分布方法[2]計算復雜、不易操作,將對原分布的統計推斷的難度轉移到了參數分布計算上。
最大熵方法因充分利用了各種先驗信息并盡量避免了引入其他不確定因素而受到重視,許多學者為之作出不懈努力。Mazzuchi等[3]將非參數的 Dirichlet函數與最大熵相結合,提出了MED先驗分布;Kazama等[4]將最大熵方法應用到不等式約束規劃問題中。Agrawal等[5]提出一種基于矩約束的最大熵雙參數聯合分布的確定方法,但該研究局限于一階矩約束。目前,關于一般形式下雙參數的最大熵先驗信息解的研究還鮮見報道。本文基于雙參數二階矩約束,求取了最大熵先驗信息解析解,并將之應用于數控系統可靠性評估中。
1 利用最大熵方法確定聯合先驗分布
如上所述,數控系統失效時間服從雙參數Weibull分布 ,即
f(t;η,m)=m exp(-(t/η)m)/[η(t/η)m-1] t >0
它有η、m兩個參數,其中,η為特征壽命(分布的0.632分位數);m為形狀參數,對密度函數形狀有很大影響。
根據二元聯合熵的定義和最大熵原理,確定雙參數聯合先驗分布 π(η,m),滿足

參數滿足的約束條件如下:

式中,ηi、mj分別為兩參數η、m的 i階和 j階原點矩;k、n分別為兩參數原點矩的最高階數,可以相同,也可以不同。
對聯合密度函數π(η,m)的求解是個泛函意義下的條件極值問題。構造如下輔助泛函:
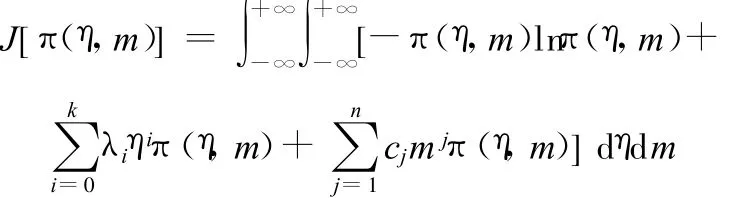
式中,λ0、λ1、…、λk、c1、…、cn為拉格朗日乘子。

本文主要討論二階矩約束下雙參數聯合先驗分布 ,對于一般的k 、n,系數λ0、λ1、…、λk、c1、…、cn可通過數值計算[6]求得。故在二階矩約束下,即當k=n=2時,先驗函數形式為

2 雙參數二階矩先驗分布的確定和穩健性分析
利用最大熵方法求解雙參數聯合先驗分布過程中,需要參數樣本的二階矩信息。由于試驗所得數據為數控系統失效時間,故本文利用自助法,通過構造再生子樣來獲取兩參數η、m的二階矩估計。詳細過程可參見文獻[7]。
在應用先驗分布前,必須分析其對后驗統計推斷結果的影響,即分析先驗分布的穩健性。一種簡單常用的先驗分布穩健性判斷方法[8-9]就是利用相對似然邊際分布函數m*(t|π)。該相對似然函數邊際分布值代表以π(η,m)為先驗分布時現場樣本出現的相對概率。當獲得現場樣本(t1,t2,…,tN)后,可計算m*(ti|π)(i=1,…,N)。如果所得值都不是非常小(一般不小于10-3),則說明先驗分布符合現場數據條件,即可以認為先驗分布π(η,m)是穩健的。
對雙參數Weibull分布,聯合先驗分布 π(η,m)的相對似然邊際函數為
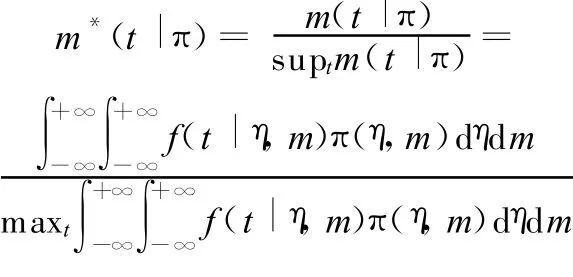
3 最大熵先驗信息解在數控系統可靠性評估中的應用
據Bayes原理,設有數控系統壽命數據T=(t1,t2,…,tN),則其似然函數可表示為
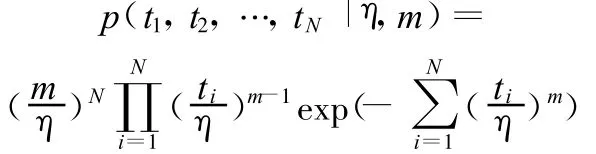
利用已知先驗形式,則參數η、m聯合后驗分布可表示為
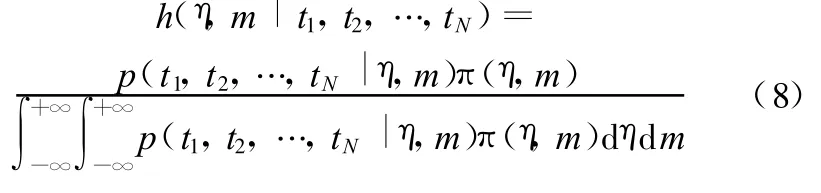
借助于數值計算,可以得到后驗分布的點估計:

最后根據Weibull分布性質可知,數控系統平均后驗無故障工作時間的估計為
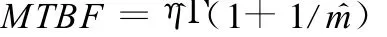
設有數控系統失效數據30個,如表1所示,利用這30個歷史數據,應用自助法生成200個容量為1000的自助樣本組,即求得η和m的參數序列,進一步可以計算兩參數的數學期望和方差:

表1 數控系統壽命數據 h
η=3811.6,m=1.4552,σ2η=7920.0,σ2m=0.0011
從而該Weibull分布尺度參數與位置參數的雙參數聯合先驗密度函數為

設有現場數控系統的壽命數據20個,如表2所示。利用該數據對先驗分布的穩健性進行驗證,計算出其相對似然邊際函數值亦如表2所示。從表2中數值可以看出,該先驗分布對于所得的現場數據而言,穩健性良好,即利用該分布作為先驗分布是可取的。將現場數據形成的似然函數乘以由歷史數據求解得到的先驗分布,得到由式(8)計算的后驗分布,并可求出其點估計:

故而數控系統平均后驗無故障工作時間的估計為
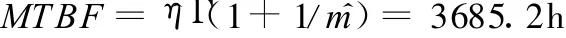
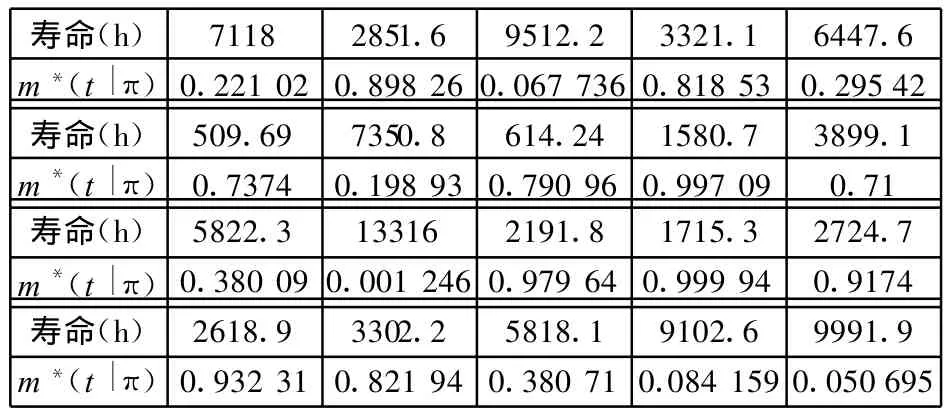
表2 現場數控系統壽命數據及其相對似然函數值
4 結語
最大熵方法能夠最大限度地利用歷史樣本信息,適用于產品壽命長、實驗數據難以獲得的高可靠性產品的評估。本文提出的基于二階矩約束、通過最大熵原理確定的先驗分布,經檢驗具有良好的穩健性。算例表明,該方法適用于數控系統可靠性評估。
[1] Ferdous J,Uddin M U,Pandey M.Reliability Estimation with Weibull Inter Failure Times[J].Reliability Engineering and System Safety,1995,50:285-296.
[2] 張湘平.小子樣統計推斷與融合理論在武器系統評估中的應用研究[D].長沙:國防科學技術大學,2003.
[3] Mazzuchi T A,Soofi E S,Soyer R.Computation of Maximum Entropy Dirichlet for Modeling Lifetime Data[J].Computational Statistics&Data Analysis,2000,32:361-378.
[4] Kazama J,Tsujii J.Maximum Entropy Models with Inequality Constraints:a Case Study on Text Categorization[J].Machine Learning,2005,60:159-194.
[5] Agrawal D,Singh J K,Kumar A.Maximum Entropy-based Conditional Probability Distribution Runoff Model[J].Biosystems Engineering,2005,90(1):103-113.
[6] 夏新濤,陳曉陽,張永振,等.航天軸承摩擦力矩的最大熵概率分布與bootstrap推斷[J].宇航學報,2007,28(5):1395-1400.
[7] 張金槐,劉琦,馮靜.Bayes試驗分析方法[M].長沙:國防科技大學出版社,2007.
[8] Berger JO.統計決策論及貝葉斯分析[M].賈乃光,譯.北京:中國統計出版社,1998.
[9] 余禮軍,Ben Heydecker.基于概率加權矩與最大熵原理的交通流統計分布估計方法[J].公路交通科技,2008,25(2):113-133.

