基于運費結構的多式聯運方式選擇研究

李 愈，李美彥，趙 軍

（1.西南交通大學峨眉校區 交通運輸系，四川 峨眉山 614202；2.西南交通大學 交通運輸學院，四川成都 610031）

伴隨通交運通輸運方輸式業的的技逐術步經發濟展優，勢充，分實發行揮多各種種運交輸方式共同參與一類貨物的運輸，是加快貨物流通速度、提高各種運輸方式設施使用效率、實現交通運輸可持續發展的有效措施。多式聯運經營者在進行貨物承運時，有的運輸方式的運輸速度較快，但運輸費用較高；有的運輸方式的運輸費用較低，但運輸速度較慢。因此，需要對各種運輸方式進行合理搭配，在滿足貨主對所承運貨物各種運輸需求的前提下，使自身經營費用最低。這種決策問題被稱為多式聯運方式選擇問題。既有文獻對多式聯運方式選擇問題做了系統研究。張運河等[1]研究了不受限的單目標問題，并且通過網絡抽象描述，將該問題轉換為廣義最短路問題，可以借助于最短路精確算法求解；部分學者研究了送達時間和運輸能力受限的單目標問題[2-7]，其中，有學者根據問題特點設計了基于最短路問題的近似求解算法[2-5]，王玲玲等[6]采用0－1編碼設計了遺傳算法，孫華燦等[7]考慮了貨物送達延誤懲罰和中轉次數限制，給出了求解思路；姜軍等[8]研究了送達時間受限的單目標問題，對具有中轉延誤的情況進行了建模分析，設計了遺傳算法；還有學者研究了貨物送達具有時間窗的能力受限單目標問題，設計了遺傳算法[9-10]，其中，賀竹磬等[9]采用整數編碼，李麗等[10]采用0－1編碼；此外，井祥鶴等[11]研究了能力不受限的多目標問題，設計了遺傳算法。以上所有文獻只考慮了運輸費用的變動部分，沒有充分考慮各種運輸方式的運輸費用結構，忽略了其固定部分，通過分析既有文獻研究，對運輸費用進行更為準確的建模分析，以期對多式聯運方式選擇問題做出更加符合實際的描述。

1 多式聯運方式選擇問題的描述

多式聯運方式選擇主要研究的問題為：多式聯運經營者需要將一批運輸量為 Q，送達時間窗為 [E，L] 的貨物從該貨物的始發城市 O 運送到目的城市 D，已知運輸路徑，路徑將途經 n 個不同的城市，任意2個相鄰的城市之間都有 g 種運輸方式可供選擇，已知各種運輸方式的運輸費用 (固定費用和變動費用)、運輸時間和運輸能力。當貨物從始發地出發時，或在任意城市從一種運輸方式轉換到另一種運輸方式時，運輸費用由固定費用和變動費用兩部分組成；其他情況下，運輸費用只包括變動費用。當貨物在任意城市從一種運輸方式轉換到另一種運輸方式時，需要一定的中轉費用及中轉時間，已知中轉費用和時間。在滿足送達時間和各種運輸方式運輸能力限制的前提下，確定各種運輸方式的最佳搭配，使得包括運輸費用、中轉費用和送達早點或延誤懲罰費用 (簡稱送達懲罰費用) 的總費用最低。利用圖論知識，將多式聯運方式選擇問題抽象為網絡 G =[V，E，W]，式中，V 為頂點集合，E 為弧集合，W 為弧權重集合。多式聯運虛擬運輸網絡如圖1所示。

頂點集 V 包括始發城市 O，城市擴展集合和虛擬目的城市 D′ 組成，在已知的運輸路徑上，除始發城市 O 外，將其他每個城市分別擴展為 g 個城市，分別表示 g 種運輸方式 (例如 V11,V12,...,V1g)。弧集 E 包括始發城市與途經第一個城市的弧集E1(例如)，除始發城市外各個途經城市間弧集 E2(例如) 和目的城市與虛擬目的城市間弧集 E3(例如。弧權重 W 由運輸費用、運輸時間和運輸能力的三元組構成，除了弧集 E3外，其余弧的運輸時間、運輸費用和運輸能力分別等于弧所對應的兩相鄰城市采用某種運輸方式時的運輸費用加中轉費用、運輸時間加中轉時間、運輸能力，弧集 E3的運輸費用和時間等于 0，運輸能力為無窮大。這種網絡抽象描述方法適用于各個途經城市可供選擇的運輸方式和運輸方式總數不同的情況，為了保證結果的合理性，需要將不存在中轉方式所對應的弧的費用和時間設為無窮大，運輸能力設為 0。通過網絡抽象描述，多式聯運方式選擇問題可以轉換為具有時間窗和能力約束的最短路問題。

2 優化模型

模型的假設為：①同一支貨流在其途經路徑上兩相鄰城市間不能分割，也就是在兩相鄰城市間只能選擇一種運輸方式；②任意兩相鄰城市間至少存在1種運輸方式。

以運輸費用、中轉費用和送達懲罰費用最小為目標，考慮送達時間窗和運輸能力的約束，建立多式聯運方式選擇問題的優化模型為：

式中：n 為運行路徑上城市集合，按照運輸路徑前進方向依次編號；g 為運輸方式集合；，，，分別為相鄰城市 i 和 i+1 選擇第 k 種運輸方式的固定運輸費用、變動運輸費用、運輸時間和運輸能力；和分別為在城市 i 從第 k 種運輸方式轉換到第 l 種運輸方式的中轉費用和中轉時間；T 為運送貨物花費的總時間；α 和 β 分別為貨物送達早點和延誤的懲罰費用系數。為 0－1 變量，若在相鄰城市 i 和 i+1 選擇第 k 種運輸方式，=1，否則，=0；為0－1變量，若在城市i從第 k 種運輸方式轉換到第 l 種運輸方式，=1，否則，=0；z1為0－1變量，若貨物送達時間早于規定時間 e， z1=1，否則，z1=0；z2為0－1變量，若貨物送達時間晚于規定時間 l 時，z2=1，否則，z2=0。

公式⑴為目標函數，表示運輸費用、中轉費用和送達懲罰費用的總和最小。其中，運輸費用由前2項算式構成，分別表示運輸過程中所需要花費的固定運輸費用和變動運輸費用，第1個算式表明只有當貨物從始發地出發或在途經任意城市從一種運輸方式轉換到另一種運輸方式時，需要支付所選擇的運輸方式的固定費用。公式⑵—⑾為約束條件，公式⑵限制運送貨物時，在途經兩相鄰城市間只能選擇一種運輸方式；公式⑶為在每一個途經城市只能選擇一種運輸方式進行后續運輸；公式⑷確保貨物運送的連續性，同時描述決策變量之間的邏輯關系；公式⑸為貨物運送時間的計算方法；公式⑹為運輸能力約束；公式⑺—⑻為貨物送達時間與時間窗之間的邏輯約束；公式⑼—⑾為變量定義域約束。

s.t. 多式聯運方式選擇問題優化模型中公式⑵、⑶、⑷、⑹、⑼

與既有研究方法相比，上述模型更具有一般性，而且能充分反映各種運輸方式的運輸費用結構。模型⑴—⑾為 0－1 非線性規劃模型，對于此類模型，盡管現階段不存在精確算法，但隨著現代數學優化理論的不斷發展和計算機能力的不斷提高，對于中小規模的問題實例，現有的各種商業優化軟件能夠勝任求解工作；對于大規模問題實例，與既有研究相比，該模型的數學性質沒有變化。因此，可以直接移植現有近似求解算法，如遺傳算法，根據初步研究結果，建議采用整數編碼方法。通過介紹基于各種運輸方式的運輸費用結構的前提下，多式聯運方式選擇問題的建模方法，采用商業優化軟件 LINGO 對1個小規模問題實例進行算例分析，說明模型的優越性。

3 算例分析

假設某多式聯運經營者需要將一批運輸量為100單位，送達時間窗為 [45 50] 單位的貨物從始發城市1運送到目的城市8，途經8個城市。各相鄰城市間各運輸方式的運輸費用、運輸時間和運輸能力見表1。貨物中轉費用和時間見表2。貨物送達早點和延誤的懲罰費用系數 α 和 β 分別為 3單位和2單位。

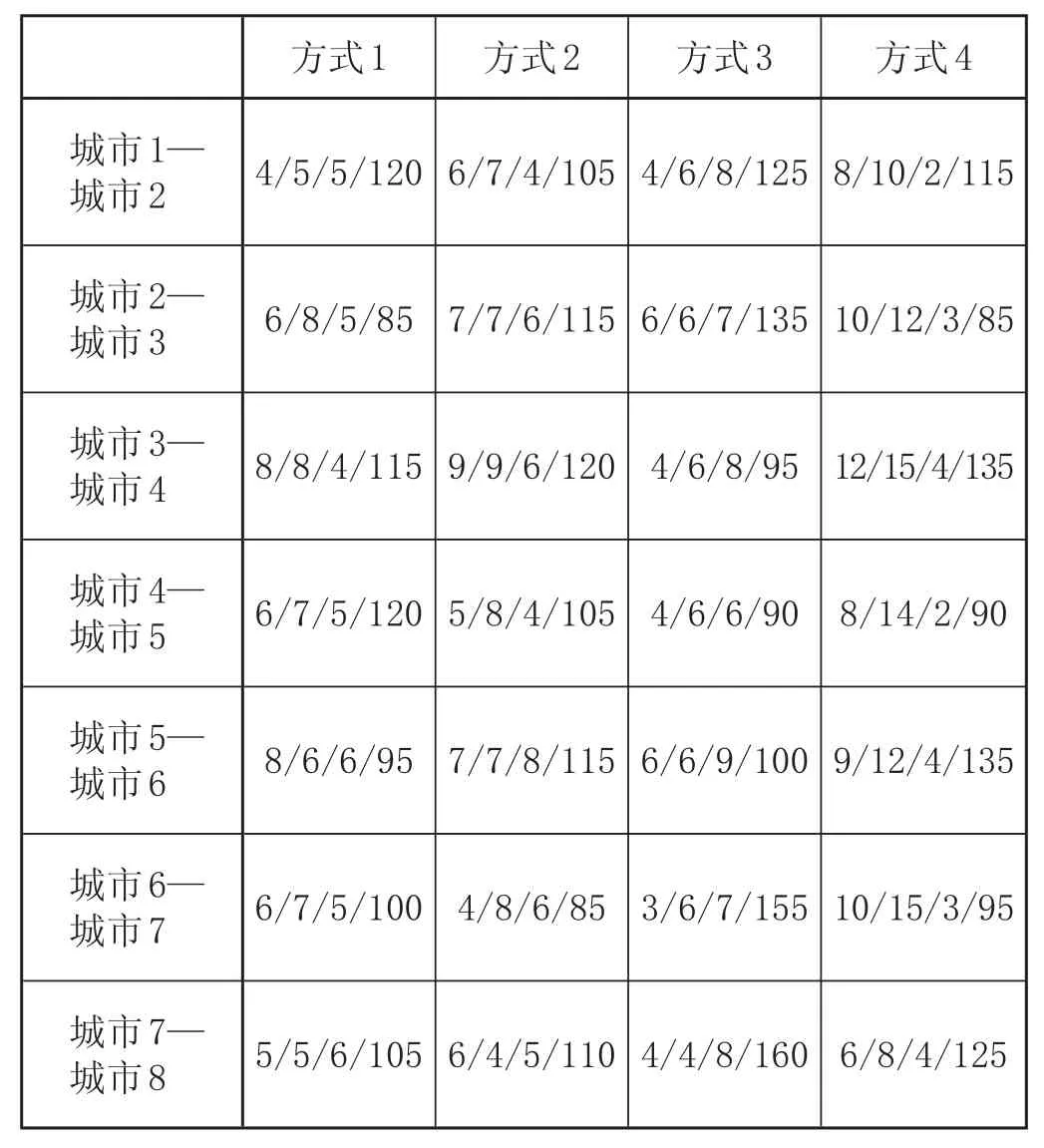
表1 相鄰城市間各運輸方式的運輸費用、運輸時間和運輸能力

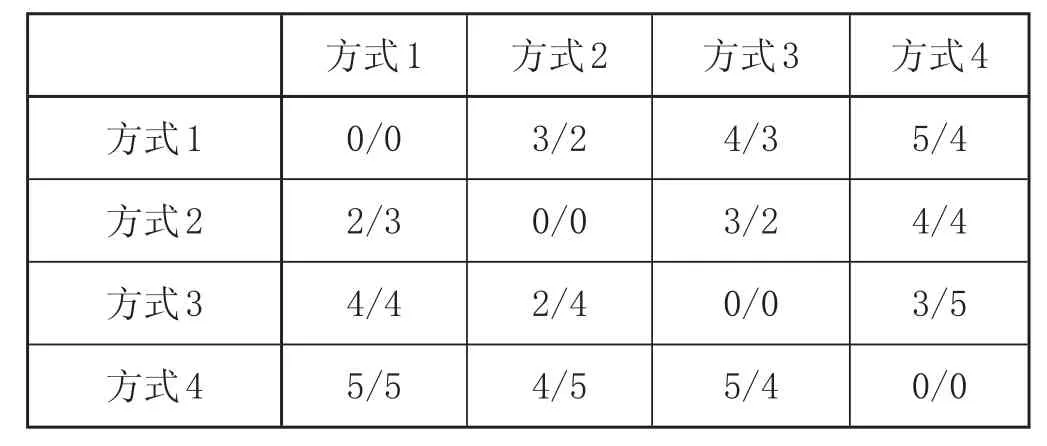
表2 貨物中轉費用和時間

利用 LINGO11.0 編程，可以找到局部最優解。計算結果為：，。這表明：采用運輸方式2將待運送貨物從始發城市1運送到城市 6，然后由運輸方式3運送到目的城市 8。送達時間為45單位，總費用為 60 單位，其中，運輸費用、中轉費用和送達懲罰費用分別為 57 單位、3 單位和0單位，運輸費用中固定費用和變動費用分別為9單位和 48 單位。

4 結束語

結合各種運輸方式的運輸費用結構，研究了多式聯運中運輸方式的合理搭配問題。與既有研究方法相比，建立了更為一般的優化模型。對于中小規模問題，建議采用商業優化軟件求解；對于大規模問題實例，建議設計近似算法求解。通過采用商業優化軟件 LINGO 進行算例分析表明，在綜合考慮運輸費用組成的基礎上，多式聯運方式選擇問題的優化模型能夠找到更優解，對多式聯運方式選擇問題進行更為符合實際的描述和建模分析。

[1]張運河，林柏梁，梁 棟，等. 優化聯合運輸問題的一種廣義最短路方法研究[J]. 鐵道學報，2006，28(4)：22-26.

[2]張得志，凌春雨. 多種運輸方式的組合優化模型及求解算法[J]. 長沙鐵道學院學報，2002，20(4)：71-75.

[3]王 濤，王 剛. 一種多式聯運網絡運輸方式的組合優化模式[J]. 中國工程科學，2005(10)：46-50.

[4]賀國先. 集裝箱公鐵聯運的費用加權最短路計算機算法[J].鐵道學報，2006，28(1)：1-5.

[5]范志強，莊佳芳. 基于多維有向圖的多式聯運中運輸方式的選擇研究[J]. 物流技術，2006，26(5)：47-48，60.

[6]王玲玲，覃運梅. 多式聯運的運輸方案選擇研究[J]. 鐵道運輸與經濟，2009 ，31(10)：78-81.

[7]孫華燦，李旭宏，陳大偉，等. 綜合運輸網絡中合理路徑優化模型[J]. 東南大學學報，2008，38(5)：873-877.

[8]姜 軍，陸 建. 集裝箱多式聯運系統中各種運輸方式最優組合模式研究[J]. 物流技術, 2008，27(4)：127-129，134.

[9]賀竹磬，孫琳巖，李曉宏. 時效性物流聯運方式選擇模型及其算法[J]. 管理科學， 2007，20(1)：8-12.

[10] 李 麗，曾永長. 物流運輸中多式聯運模型及算法[J]. 統計與決策，2009(20)：27-29.

[11] 井祥鶴，魏冬峰，周獻中. 運輸方式選擇多目標優化問題的混合遺傳算法[J]. 計算機工程與應用，2008，44(6)：210-212，224.