無線自組網個體移動模型分析

劉宴濤，安建平，盧繼華，劉珩

（1.渤海大學 信息科學與工程學院 計算機網絡智能重點實驗室，遼寧 錦州 121013；2.北京理工大學 電子工程系，北京 100081）

1 引言

移動模型是無線自組織(ad hoc)網絡仿真研究的重要工具，用以規劃節點的移動軌跡。根據移動方式的不同，ad hoc網絡的移動模型一般可以分為2大類[1]。如果網絡中節點彼此獨立地選擇自己的運動參數，如速度和方向等，則這種模型被稱為個體移動模型；如果節點以某種合作的、相互依賴的方式移動，則稱之為群組移動模型。個體移動模型以節點運動的隨機性為特征，這類模型具有遍歷性，即對某一個節點在多個時刻的采樣和多個節點在同一時刻的采樣具有相同的分布。

隨機點模型、隨機游走模型和隨機方向模型是3種典型的個體移動模型，其中隨機點模型應用最廣泛。最近研究發現該模型具有非均勻節點分布[2,3]和速度衰減[4]等問題，這反映出使用該模型的仿真網絡存在一段時期的瞬態過程，該過程可能持續很長時間，以至于在有限時間內收集到的結果不可信。由于準確的仿真應該工作在系統的穩態，所以深刻理解和準確把握移動模型的穩態特征對于規避模型的瞬態過程，有效設計一個無線自組網仿真來說是至關重要的。目前針對個體移動模型的穩態特征已經開展了一些研究，Bettstetter[3]分析了隨機點模型的節點分布特征，得到了一維區間的精確解和二維區域的近似解。Lin[5]利用更新理論研究了隨機點模型的節點速度分布，得到了節點平穩速度分布的概率密度函數的解析解，從而解釋了隨機點模型的速度衰減問題。Boudec[6]開創性地把 Palm積分引入到ad hoc網絡移動模型的特性分析中，得到了隨機點模型在平穩狀態下速度分布和節點分布的精確解。Garetto[7]應用偏微分方程描述隨機游走模型的特征，包括系統的瞬態行為和收斂速率。此外，還有大量的仿真工作對模型的穩態特征加以驗證。

從隨機過程的角度來看，各種模型的工作過程構成了隨機點過程。Boudec[6]通過對隨機點模型的分析證明，只要模型的速度下限Vmin大于0，點過程就存在平穩態，該結論對其他2個模型也成立。因此，可以把平穩點過程的方法和結論應用到個體移動模型的穩態速度分布和節點分布的分析中。本文以上述3種模型的平穩速度分布和節點分布為研究對象，采用理論分析和實驗仿真相結合的方法加以分析，主要工作包括如下：

1) 應用Palm積分分析3種模型的平穩速度分布，證明距離型隨機游走模型、隨機點模型和隨機方向模型節點速度的時間平均低于事件平均，從而具有速度衰減問題，并總結具有這種問題的移動模型的本質特征；

2) 應用幾何概率分析隨機方向模型的平穩節點分布，得到圓形區域下節點分布的閉式解；

3) 應用Palm積分分析一維區間隨機點模型的平穩節點分布，得到概率密度函數的閉式解；

4) 應用中心極限定理推導隨機游走模型在無邊界區域的端點分布。

后續內容安排如下：第2節簡要介紹了3種移動模型的工作方式；第3節簡介本文采用的2個主要數學工具，即幾何概率與 Palm積分的相關理論和結論；第4節對3種模型的速度衰減問題加以分析；第5節、第6節分別針對隨機方向模型和隨機點模型的平穩節點分布加以分析；第7節給出了無邊界區域下隨機游走模型的端點分布；第8節是結束語。

2 Ad hoc網絡個體移動模型介紹

2.1 隨機點模型(RWP,random waypoint model)

隨機點模型采用分段移動軌跡，每一段軌跡被稱為一個運動周期。仿真開始后，每個節點在仿真區域內部隨機選擇一個目的點，然后以速度v向目的點移動，v均勻產生于區間[Vmin,Vmax]。到達目的點后節點暫停，然后開始下一周期。

2.2 隨機游走模型(RW,random walk model)

隨機游走模型也采用分段的移動軌跡。但與隨機點模型不同的是在隨機游走模型中，節點從當前位置選擇一個隨機方向和隨機速度，移動一段距離或一段時間后暫停，然后變換方向開始下一周期。在有邊界區域，如果移動過程中節點撞到了區域邊界，則它將被反射回區域內部。隨機游走模型目前還沒有一個標準的定義，本文把該模型分為2個子類型：

時間型(RW1)，在一個周期中節點的移動時間服從某種分布。

距離型(RW2)，在一個周期中節點的移動距離服從某種分布。

2.3 隨機方向模型(RD,random direction model)

文獻[7～9]也把隨機游走模型稱為隨機方向模型。為避免混淆，本文中術語“隨機方向”專指Royer模型，該模型由E.M.Royer[10]于2001年提出，曾被文獻[1,2]所引用。該模型的移動特點是節點在區域內部不能停留，即一個周期只能開始并結束于區域的邊界，所以節點的移動軌跡由區域的弦構成。

3 幾何概率與積分

3.1 幾何概率

幾何概率源于2個世紀以前的Buffon針問題，該理論把概率的思想應用到隨機幾何對象上，如點、線等[11]。在幾何概率中，平面上的一條直線由其到原點的距離p和其法線與x軸夾角θ所決定，直線方程定義為[11]

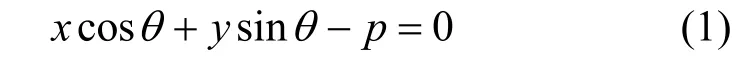
幾何概率把dp dθ作為直線集合的密度，把∫Kdp dθ作為區域K中直線集合的測度，這是唯一滿足剛體運動群不變性的密度和測度定義[11]。幾何概率的一個結論是與閉凸集K相交的直線集合的測度滿足[12]：

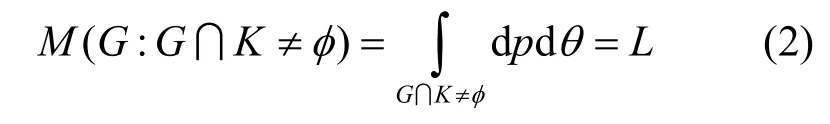
其中，M(·)表示集合的測度，L是K邊界的周長。

3.2 Palm積分

對一個仿真系統的采樣可以基于2種時鐘：標準時鐘和事件時鐘[6,13]。標準時鐘是均勻流逝的，具有無限精度的時鐘；事件時鐘的推進則依靠仿真事件的發生。根據參考時鐘的不同，可以通過時間平均和事件平均2種方法來統計仿真結果，這2種結果往往是不一致的。

事件平均

時間平均

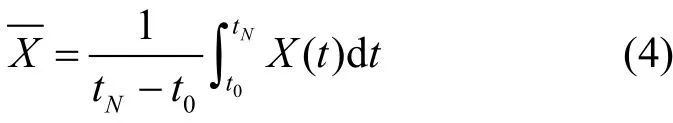
當滿足速度下限非零的條件時，移動模型可以建模為平穩點過程[6]。圖1給出了移動模型的點過程表示，假設經過一段仿真時間后，在觀察的起始時刻（以0表示）仿真系統已經處于穩態，并令t0和t1分別是0時刻之前和之后的狀態轉移時刻，即t0≤0＜ t1。

圖1 移動模型的點過程

Palm積分[13,14]是分析平穩點過程的重要工具，Palm期望和Palm概率定義為[13]

E0(X)=E(X |在 0時 刻有事件發生)P0(X ∈ W)=P(X ∈ W|在 0時 刻有事件發生)

用平穩更新過程的術語來說，Palm分布相當于在原點有更新事件發生的條件概率分布[14]。若X滿足遍歷性，則X的時間平均趨近于期望E(X)，事件平均0趨近于Palm期望E0(X)[13]。下面不加證明地給出與移動模型分析相關的2個Palm積分公式[13]：

其中，λ代表平穩點過程的點密度。本文的第4節和第6節采用的主要就是Palm積分的分析方法。

4 個體移動模型的速度衰減問題

4.1 RW1模型的平穩速度分布

下面的分析假設在觀察的起始時刻(設為 0時刻)，系統已經處于穩態。在RW1模型中，節點每個周期的移動時間Ti服從某種分布(比如指數分布)。在每段軌跡的終點，節點選擇下一次移動的速度Vi，Vi服從[Vmin，Vmax]區間的均勻分布，隨機變量 Vi和 Ti相互獨立，則其速度的時間均值和事件均值分別為

應用反演公式可得：

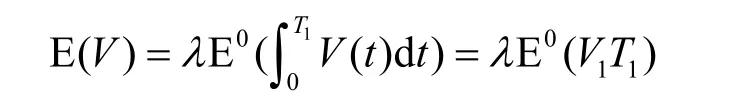
根據隨機變量V1和T1的獨立性，并利用密度公式 λ=1/E0(T1)，可得

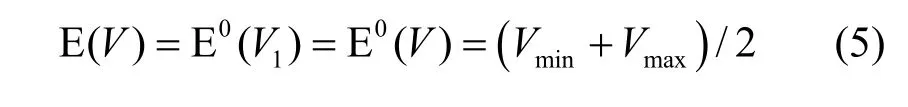
可見，RW1模型處于穩態時，節點速度的時間均值和事件均值相等，不存在速度衰減問題。

4.2 RW2、RWP和RD模型的平穩速度分布

RW2模型要求節點在每一周期的移動距離服從某種分布，下面的分析假設周期移動距離為定值L，其速度的時間均值和事件均值分別為

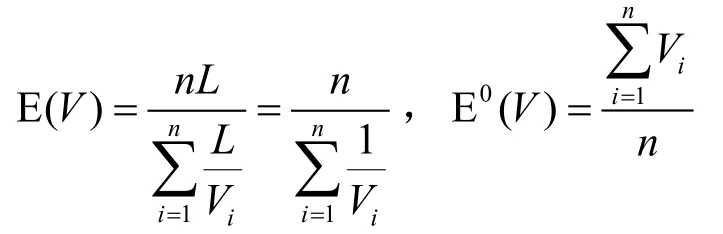
由反演公式可得 E(V)=λE0(V1T1)

以c表示隨機變量V1和T1的協方差，即

則

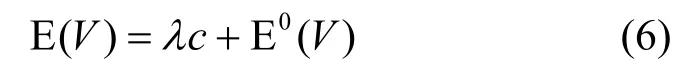
仿真設置：速度范圍是[0，5] m/s，所以速度的事件均值應為2.5m/s。第一個實驗仿真RW1模型的時間平均速度，移動周期固定為10s，每秒采樣一次取時間平均，如圖2所示。第二個實驗對RW2模型的節點速度在每個周期端點處采樣，結果取事件平均，如圖3所示；第三個實驗對RW2模型的節點速度每秒采樣一次，結果取時間平均，如圖4所示。結果表明，RW1模型不存在速度衰減問題，而RW2模型則存在。

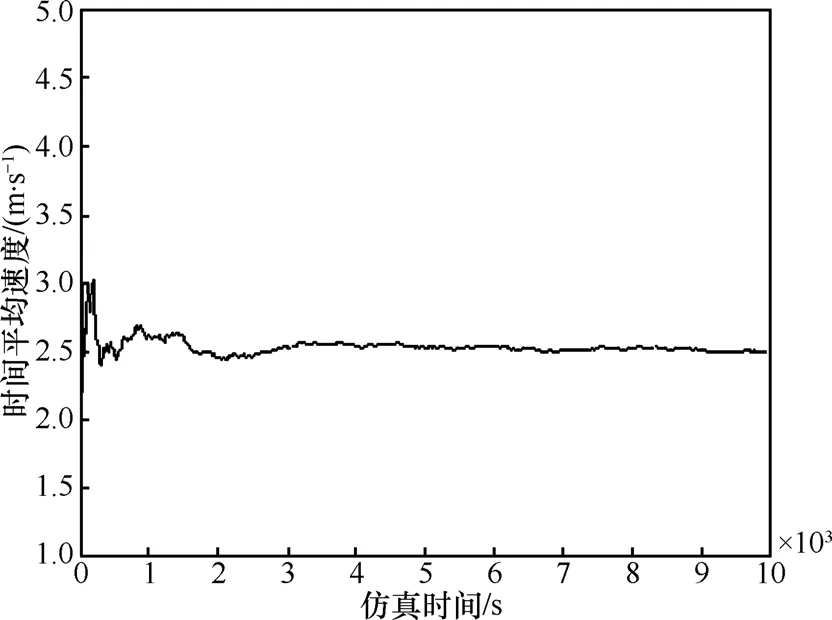
圖2 RW1模型節點速度的時間平均仿真

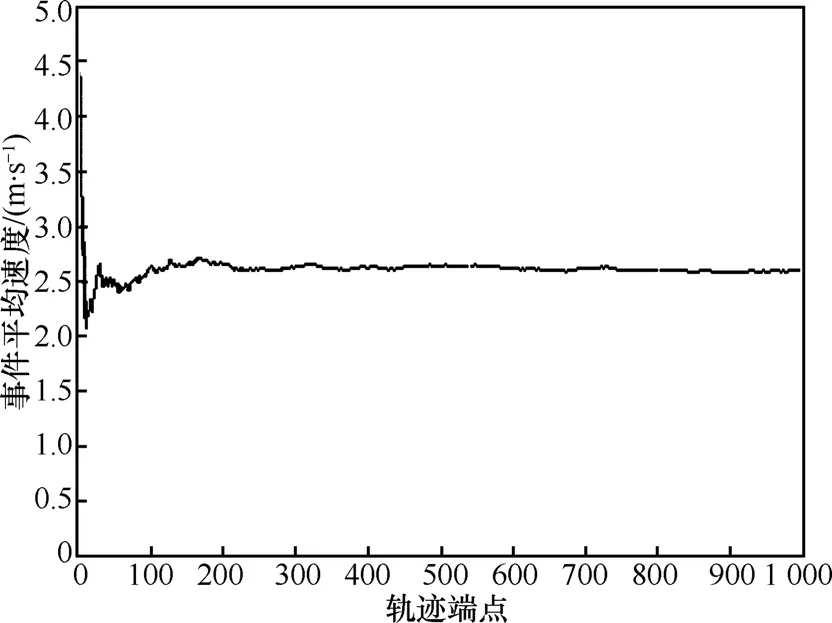
圖3 RW2模型速度的事件平均仿真

圖4 RW2模型速度的時間平均仿真

進一步，基于Boudec對RWP模型所做的工作可得RWP，RW2，RD模型平穩速度分布的概率密度函數形如其中E0(L)表示節點分段軌跡長度的事件平均。假設仿真區域是半徑為 r的圓形區域，對于 RWP模型，E0(L)應該等于區域內2個隨機點之間的平均距離，由幾何概率[11]可知E0(L)＝128r/45π。對于RD模型，E0(L)應該等于區域邊界上2個隨機點之間的平均距離，由數學中隨機弦問題[15]可知E0(L)＝4r/π。所以3種模型時間平均速度分布的概率密度函數為

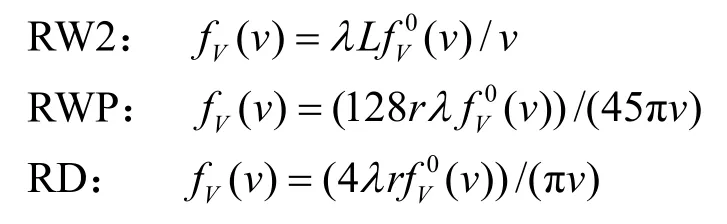
可見，在RW2、RWP和RD模型中，節點平穩速度分布的概率密度函數與v成反比，如圖5所示，這意味著對某一個節點來說，它會以很高的概率位于較低的速度區間，而以較低的概率位于較高的速度區間，這也驗證了速度衰減現象。

圖5 RW2模型的時間平均速度分布和Palm分布

4.3 速度衰減問題小結

比較式(5)、式(6)可見，在RW2、RWP以及RD模型中，每個運動周期的移動速度Vi和該周期持續時間Ti的相關性造成了速度的事件平均和時間平均不一致，從而導致速度衰減現象。對這個現象的直觀解釋是：在這3種模型中，節點在每個周期的移動距離服從相同分布，這就造成速度較低的周期持續時間較長，因此在對速度取時間平均時被分配了較大的權重，從而時間平均速度會向低速區間推移。

5 隨機方向模型的平穩節點分布

因為RD模型的節點移動軌跡由仿真區域的弦構成，所以應用概率語言可以把RD模型的平穩節點分布問題等價地描述為：在區域K全部弦構成的集合中，隨機選擇一根弦G并在其上隨機選擇一點Q，如圖6所示，則隨機點Q與RD模型中節點的瞬時位置具有相同的概率分布。下面以圓形區域為例做出具體分析。在圖6中，弦G表示節點在某個周期的移動軌跡。K是半徑為R的圓形仿真區域，K1是半徑為r

圖6 隨機弦G上的隨機點Q的分布同于節點的時間平穩分布

的同心圓，Q是G上的一個隨機點。根據圓形區域各向同性的特點，定義隨機變量d表示隨機點Q與圓心的距離。CDF(r)＝Pr(d≤r)是 d的累積分布函數，它等于Q落在K1內部的概率。以l(K)和l(K1)

分別表示G被K和K1所截得弦的長度，以M(K)表示區域K弦集的測度，根據式(2)，M(K)應等于K的周長，即 2πR。對于坐標為(p,θ)的弦 G，其上隨機點Q位于K1內部的概率為

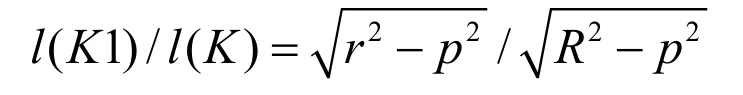
因此，累積分布函數CDF(r)為

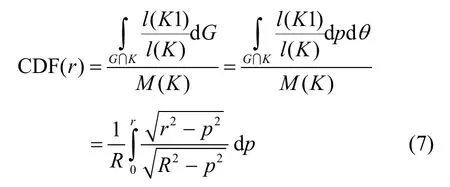
把(r/R)替換為k，則k相當于R歸一化時的r。把(p/R)替換為ksinφ，則上式可以化為

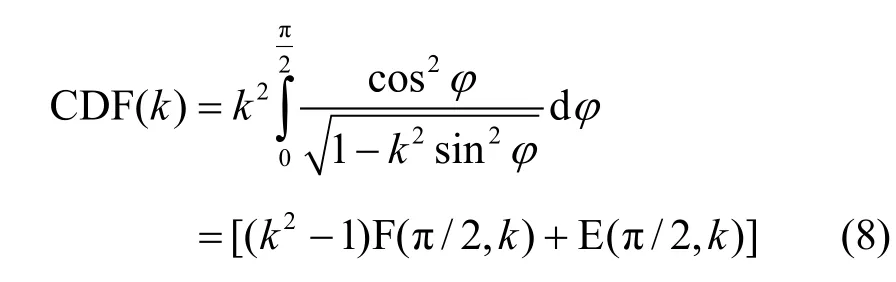
其中，F(φ，k)和 E(φ，k)分別被稱為橢圓積分的第一和第二類Legendre標準范式[16]。特別地，F(π/2，k)=K(k)，E(π/2，k)=E(k) 又被稱為完全橢圓積分，所以式(8)可以化簡為

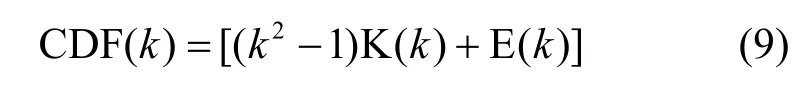
K(k)和E(k)的函數值可以查表求得[16]。圖7畫出了取 R=1(即仿真區域為單位圓)時 CDF(r)和 pdf(r)的曲線。為了比較，同時給出了均勻分布的累積分布函數(=r2/R2)和概率密度函數(=2r/R2)的曲線。圖 8給出了RD模型概率密度函數的三維視圖。可見，RD模型工作在圓形區域時，其平穩節點分布在靠近圓心的區域與均勻分布接近，但在靠近邊界的區域明顯高于均勻分布，這表明該模型節點趨于向邊界發散。

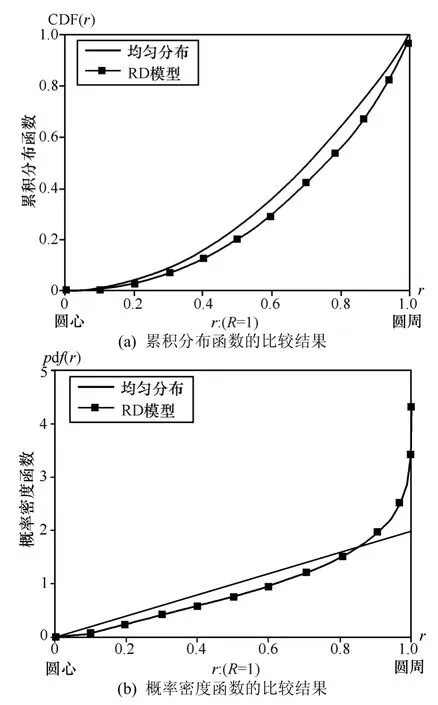
圖7 RD模型與均勻分布CDF(r)和pdf(r)的比較結果

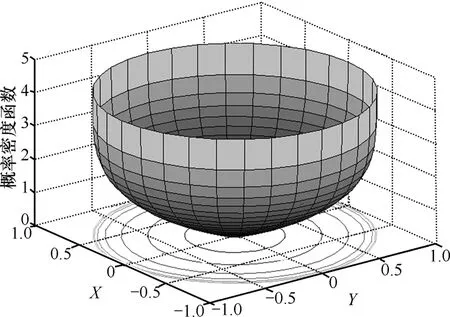
圖8 RD模型平穩節點分布的三維視圖

仿真設置：一個節點按照RD模型的移動規則在單位圓內移動，速度設為1m/s，每0.1s記錄一次節點位置，共收集20 000個位置數據，把[0,1]區間等分為10組，把樣點位置按照與圓心的距離分配到各個子區間并統計每個子區間的樣點數。為了比較，還產生了同樣數目的均勻分布的節點位置，比較結果如圖9所示。仿真結果與圖7所示的理論結果相吻合，進一步驗證了RD模型節點向邊界發散的效果。

圖9 RD模型圓形區域的仿真結果

6 隨機點模型的平穩節點分布

6.1 一維區間隨機點模型節點的時間平穩分布

一維情況下，RWP模型工作在區域[0，a]中。假設某個移動周期的起點為p，終點為n，則節點的瞬時位置x(t)應均勻分布于p和n之間，如圖10所示。

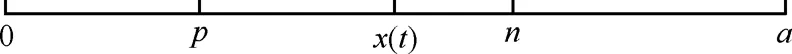
圖10 一維區間RWP模型節點分布分析

假設該周期的長度為T1，速度為V1，對于x(t)的一個有界函數f(x(t))應用反演公式可得：

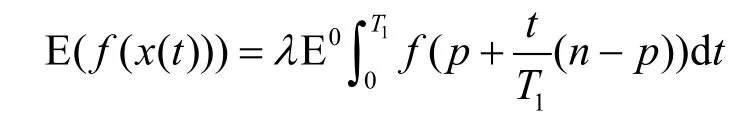
替換t/T1為u，可得：

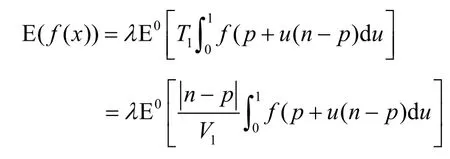
根據隨機變量p、n和V1的相互獨立性，上式化為

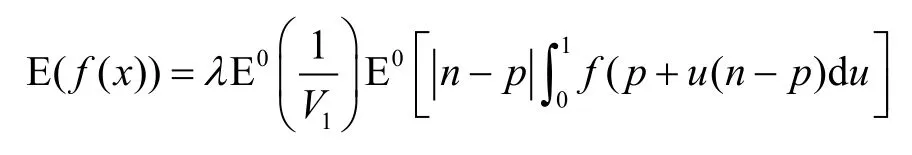
為了求解上述積分，不妨先假設 p＜n，并替換p+u(n-p)為x，則上式變為

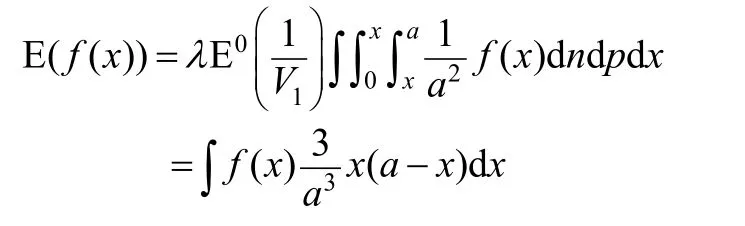
所以x的概率密度函數為 3x(a-x)/a3，再考慮到p＞n的情況，可得 pd f(x)=6x(a-x)/a3，取a=1時計算結果如圖11所示。

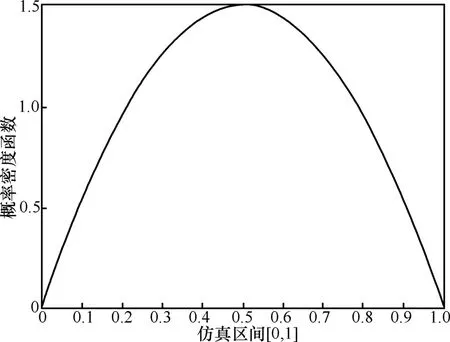
圖11 一維區間RWP模型節點分布的理論結果

一維區間仿真設置：一個節點在[0，1]區間按照RWP模型規則移動，速度均勻分布于[0.01，0.05]，對其運動軌跡每秒采樣一次，記錄樣點的位置。把[0，1]區間等分為10個子區間，統計每個子區間出現的樣點的個數，該統計量正比于節點出現在該子區間的概率，圖12為100個運動周期的仿真結果。

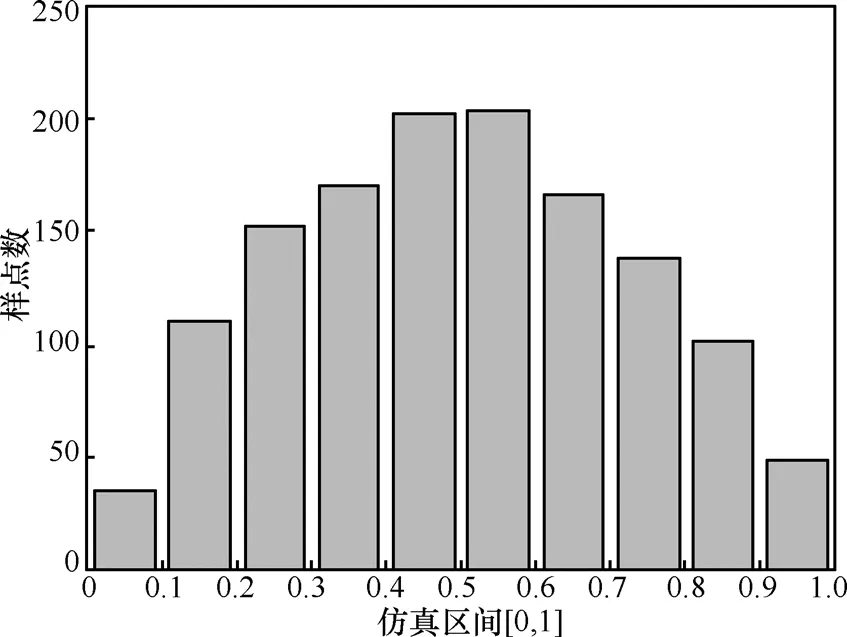
圖12 一維區間RWP模型節點分布的仿真結果

6.2 二維區域隨機點模型節點的時間平穩分布

Boudec[6]分析了二維區域 RWP模型的節點分布特征，給出二維凸區域中 RWP模型的時間平穩節點分布概率密度函數的通用表達式為

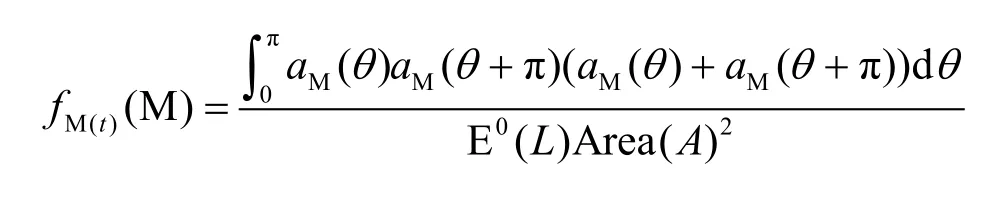
其中，E0(L)表示區域內部2個隨機點的平均距離，Area(A)表示區域A的面積，aM(θ)表示點M沿著方向θ與邊界的距離。應用此公式針對圓形區域做出具體分析，可得：

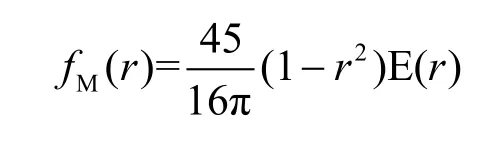
其三維視圖如圖13所示。

圖13 二維圓形區域RWP模型節點分布的理論值

仿真設置：在 RWP模型中，令目的點均勻產生于單位圓區域內，速度均勻分布于[0.01，0.05]，對其運動軌跡每秒采樣一次，記錄樣點的位置。把[-1，1]2區間等分為100×100個小格子，統計每個小格子出現的樣點的個數，該統計量正比于節點出現在各個小格子的概率。圖14所示為5 000個運動周期的仿真結果。

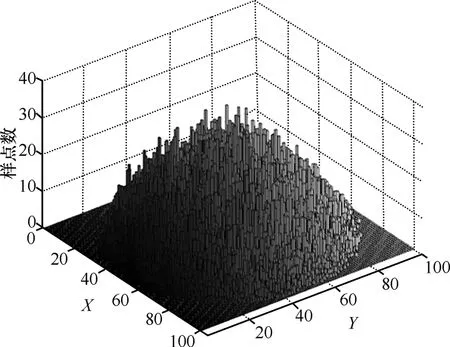
圖14 二維圓形區域RWP模型節點分布的仿真結果

7 無邊界區域RW模型的端點分布

RW模型與RWP和RD模型有所不同: 第一，RW 模型可以工作在無邊界區域；第二，RW模型的端點分布不像RWP和RD模型那樣簡單直觀。Garetto[7]和Boudec[17]對有邊界區域RW模型的節點分布問題進行了深入研究，證明該模型在有邊界區域采用反射效應或者環面效應時平穩節點分布為均勻分布。但目前對于RW模型工作在無邊界區域時的節點分布問題還有待解決。由圖15可見，RW1模型的每個運動周期由3個獨立的隨機變量T、V、φ所決定。其端點坐標為

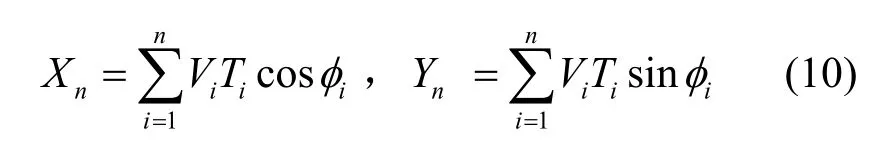
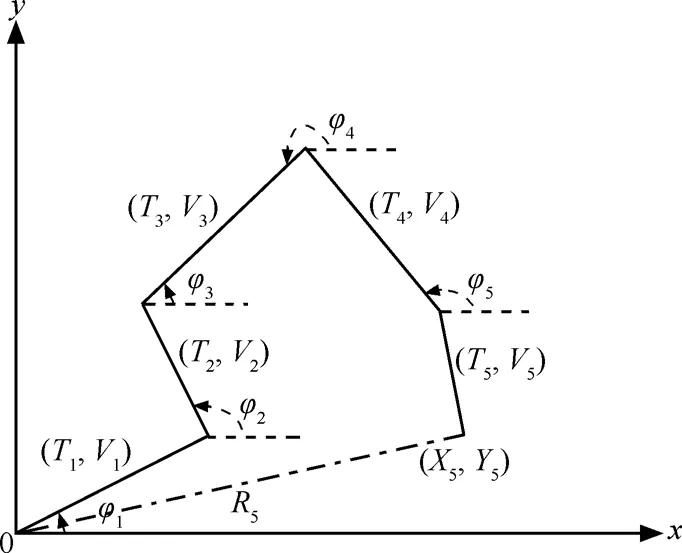
圖15 無邊界區域的RW1模型

由圖16可見，RW2模型的每個運動周期由2個獨立的隨機變量 L、φ所決定。各個移動周期的端點坐標為

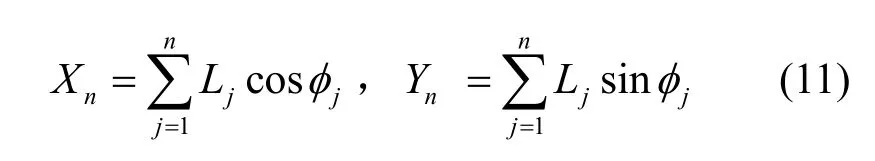
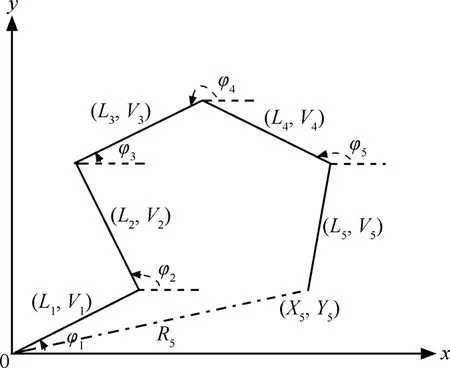
圖16 無邊界區域的RW2模型

φ服從0到2π區間的均勻分布。由式(10)中隨機變量T、V、φ的獨立性和式(11)中隨機變量L、φ的獨立性可知，無論是RW1模型還是RW2模型，Xn（或Yn）都是n個獨立同分布的隨機變量之和，根據中心極限定理，當n很大時Xn（或Yn）應趨于正態分布。以式(11)為例，假設每個周期節點移動固定長度l，則：

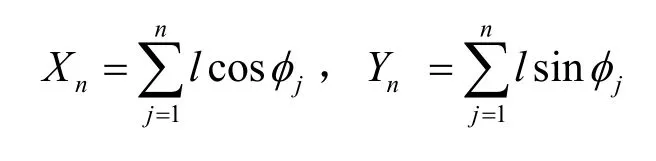
因為lcosφj的期望和方差分別為

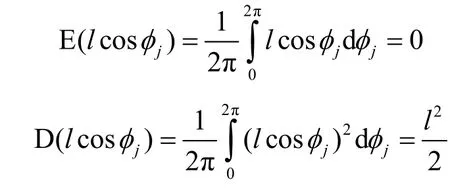
所以Xn的期望和方差為

因此，Xn的概率密度函數為

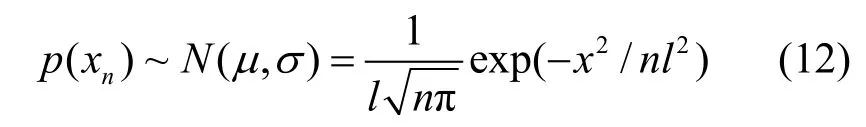
同理，Yn的概率密度函數為

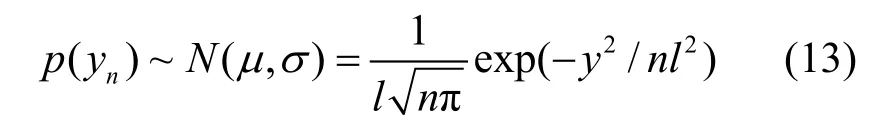
此外，Hughes[18]應用隨機矢量特征函數的方法對的分布加以分析。當移動次數在4步以內時，求出了Rn概率密度函數的精確閉式解，當移動次數很大時，求出了其近似表達式如下：

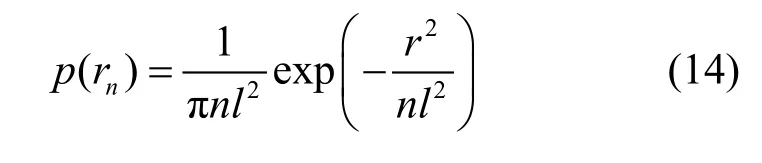
由式(12)～式(14)可見，從原點出發的某個隨機游走節點經過很多步移動后，節點與原點的距離以及節點位置的橫、縱坐標均服從正態分布。因此，如果仿真網絡全部節點的初始分布是均勻分布，那么隨著仿真時間的推進，網絡將保持均勻分布不變。

8 結束語

由前面的分析可知，只有令移動模型在各個周期內移動速度和周期持續時間彼此獨立，才能從根本上解決速度衰減問題，在本文研究的4種模型中，只有 RW1模型具有這樣的特征。其次，從平穩節點分布看，RWP模型和RD模型都表現出非均勻分布特征，即處于穩態時節點會以很高的概率出現在某個子區域，這種節點位置的耦合關系與個體移動模型獨立性和隨機性原則是相悖的，必然降低仿真的準確度。RW模型由于能夠保持節點的均勻分布，所以優于前兩者。綜上所述，時間型隨機游走模型的平穩速度分布和節點分布性能要優于距離型隨機游走模型、隨機點模型和隨機方向模型，是最理想的個體移動模型。

[1] CAMP T,BOLENG J,DAVIES V.A survey of mobility models for ad-hoc network research[A].Wireless Communication & Mobile Computing(WCMC): Special Issue on Mobile Ad-Hoc Networking:Research,Trends and Applications[C].2002.483-502.

[2] YU D,LI H.Influence of mobility models on node distribution in ad-hoc networks[A].Proceedings of ICCT[C].Piscataway,NJ,USA:IEEE Press,2003.985- 989.

[3] BETTSTETTER C,RESTA G,SANTI P.The node distribution of the random waypoint mobility model for wireless ad-hoc networks[J].IEEE Transactions on Mobile Computing,2003,2(3): 257-269.

[4] YOON J,LIU M,NOBLE B.Random waypoint considered harmful[A].Proc IEEE Infocom[C].Piscataway,NJ,USA: IEEE Press,2003.1312-1321.

[5] LIN G,NOUBIR G,RAJARAMAN R.Mobility models for ad-hoc network simulation[A].Proc IEEE Infocom[C].2004.454-463.

[6] BOUDEC J L.Understanding the Simulation of Mobility Models with Palm Calculus[R].Technical Report,2005.

[7] GARETTO M,LEONARDI E.Analysis of random mobility models with partial differential equations[J].IEEE Trans Mobile Computing,2007,6(11): 1204-1217.

[8] BETTSTETTER C.Mobility modeling in wireless networks: categorization,smooth movement,and border effects[J].ACM Mobile Comp and Comm Rev,2001,5(3): 55-67.

[9] NAIN P,TOWSLEY D,LIU B.Properties of random direction models[A].Proc IEEE INFOCOM[C].2005.1897-1907.

[10] ROYER E M,MELLIAR P M,MOSER L.An analysis of the optimum node density for ad-hoc mobile networks[A].Proceeding of the IEEE International Conference on Communications(ICC)[C].Piscataway,NJ,USA: IEEE Press,2001.857-861.

[11] SANTALO L A.Integral Geometry and Geometric Probability[M].Cambridge: Cambridge University Press,2004.

[12] SOLOMAN H.Geometric Probability[M].Philadelphia: Society for Industrial and Applied Mathematics,1978.

[13] BOUDEC J L.Performance Evaluation of Computer and Communication Systems[EB/OL].http://perfeval.epfl.ch,2009.

[14] 鄧永錄,梁之舜.隨機點過程及其應用[M].北京: 科學出版社,1992.DENG Y L,LIANG Z S.Random Point Process and Its Applications[M].Beijing: Science Press,1992.

[15] WEISSTEIN E W.Circle line picking[EB/OL].http://mathworld.wolfram.com/CircleLinePicking.html,2009.

[16] JAHNKE E,EMDE F.Tables of Functions with Formulae and Curves[M].New York: Dover Publications,1945.

[17] BOUDEC J L,VOJNOVIC M.The random trip model: stability,stationary regime,and perfect simulation[J].IEEE/ACM Trans on Networking,2006,14(6): 1153-1166

[18] HUGHES B.Random Walks and Random Environments[M].Oxford:Clarendon Press,1995.