基于盒式圖的數據過濾與回歸分析算法

杜慶峰，李 巖

(同濟大學 軟件學院，上海 200331)

軟件度量是對軟件開發項目、過程及其產品進行數據定義、收集以及分析的持續性定量化過程，目的在于對此加以理解、預測、評估、控制和改善，從而保證軟件開發中的高效率、低成本、高質量[1]。但是，得到正確的度量只是測量程序的一部分。軟件質量是與所收集和分析的數據質量密切相關的，數據清洗過程的目的就是要解決“臟數據”的問題。數據清洗是指去除或修補源數據中的不完整、不一致、含噪聲的數據。在源數據中，可能由于疏忽、懶惰，甚至為了保密使系統設計人員無法得到某些數據項的數據[2]。根據決策系統中“garbage in garbage out”(如果輸入的分析數據是垃圾則輸出的分析結果也將是垃圾)原理，必須處理這些噪聲數據。去掉噪聲平滑數據的技術主要有分箱(binning)、聚類(clustering)、回歸(regression)等[3]。本文在回歸分析的基礎上，加入了盒形圖進行數據過濾，從而得出一條線性回歸直線，使模式或者關系變得更加明顯，從而用這些模式和關系對測量的屬性作出判斷。

1 盒形圖和回歸分析簡介

1.1 盒形圖

該方法可以描述數據集取值范圍的情況，展示數據主要聚集的區域，發現離群數據可能的位置，以便于對離群數據進行處理。盒形圖顯示一個變量的信息，如對相同CMM等級的不同項目完成每個FP的工作量分析，根據中位數 m、上四分位數 u、下四分位數 l、盒長 d、和尾(tail)來分析。

中位數是在數據集中排列居中的項。也就是說，如果中位數取值為m，則數據集中有一半的值大于m，一半的值小于m。將所有數值按大小順序排列并分成四等份，處于三個分割點位置的得分就是四分位數。最小的四分位數稱為下四分位數l，所有數值中，有四分之一小于下四分位數，四分之三大于下四分位數。中點位置的四分位數就是中位數。最大的四分位數稱為上四分位數u，所有數值中，有四分之三小于上四分位數，四分之一大于上四分位數。也有叫第25百分位數、第75百分位數的。將上四分位數和下四分位數的距離定義為盒長d，因此，d=u-l。接下來定義分布的尾(tail)。理論上，上尾值點為u+1.5d，下尾值為u-1.5d，這些值必須進行舍位處理，以接近真實數據，位于上尾和下尾之外的值稱為離群值。

1.2 回歸分析方法

回歸分析方法是研究要素之間具體數量關系的強有力的工具，運用這種方法能夠建立反映要素之間具體的數量關系的數學模型，即回歸模型。線性回歸技術的基礎就是散點圖。將每個屬性對表示為一個數據點(x，y)，然后用回歸技術計算出能夠最好地擬合這些點的直線。目標是將屬性y(因變量)根據屬性x(自變量)表示為等式：y=a+bx。

線性回歸的理論是從每個點垂直向上或向下畫一條線段到趨勢直線，表示從數據點到趨勢直線的垂直距離。在某種意義上，這些線段的長度表示數據和直線的差異，且這種差異應盡可能地小。因此，“最佳擬合”的直線式是指使該距離最小的直線。

在數學上要計算“最佳擬合”直線的斜率b和截距a是很簡單的。每個點的差異稱為殘差，生成線性回歸直線的公式是殘差的平方和達到最小。可以將每個數據點的殘差表示為：

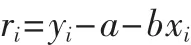
最小化殘差平方和得到以下關于a、b的等式：

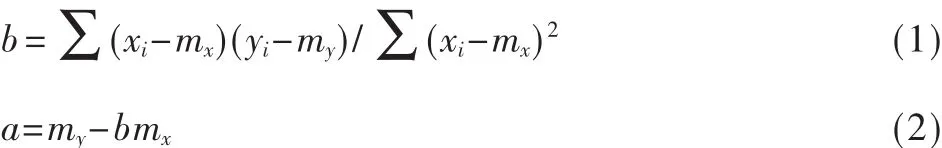
mx是 xi的平均值，my是 yi的平均值[4]。

2 算法實現

在進行數據清洗時，由于數據是無序輸入的，所以先對其排序，再用盒形圖法行數據清洗。以下是偽代碼：

接下來要對篩選出來的數據進行回歸分析，從而得到一個數據模型。

從而得到一條線性直線，算法結束。

3 算法在實驗數據上的實現

從SSMBSS(上海軟件度量基準體系)中選取了一組數據(見表1)，首先將其用散點圖列出來(見圖 1)，然后用盒形圖進行數據清洗(見圖2)，最后用回歸分析得出擬合直線(見圖 3)。

綜上所述，對于軟件度量過程中出現的數據冗余和失真的情況，可以通過數據過濾和回歸分析進行處理，除去那些離群的數據，并得出相應的擬合直線，這樣就可以分析出數據的規律，保證軟件的質量，提高效率。

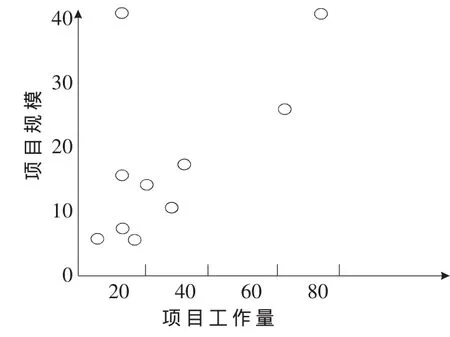
圖1 散點圖

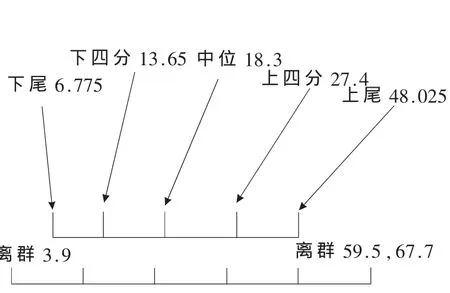
圖2 盒形圖分析結果

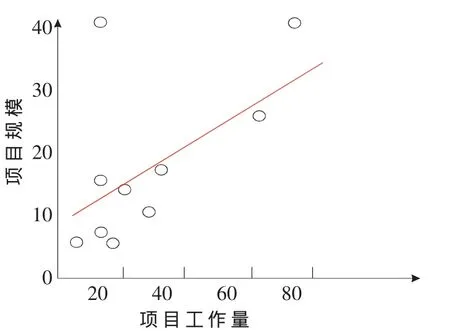
圖3 擬合直線

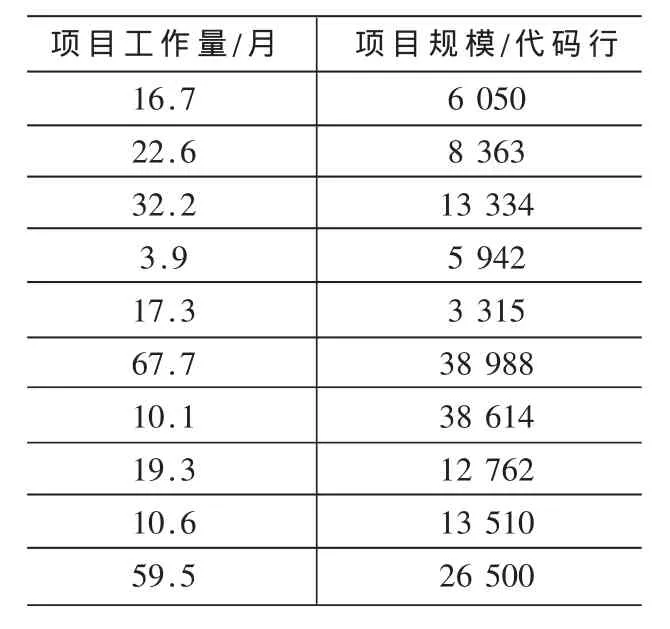
表1

[1]FENTONenton N E，PFLEEGER S L.Softwaremetrics:a rigorous&practical apporach[M](第2版).北京:清華大學出版社，2003.

[2]郭志懋，周傲英.數據質量和數據清洗研究綜述.軟件學報[J]，2002(11).

[3]王石，李玉忱，劉乃麗，等.在屬性級別上處理噪聲數據的數據清洗算法.計算機工程[J]，2005(5).

[4]徐建華.現代地理學中的數學方法.北京：高等教育出版社，2002.