讓課本習題成為數學探究的鮮活資源

●鈕兆嶺 (淮陰師院附屬中學 江蘇淮安 223001)

《普通高中數學課程標準(實驗)》明確指出：“數學探究是貫穿于整個高中數學課程的重要內容，滲透在每一個模塊或專題中”.又指出“倡導積極主動、勇于探索的學習方式”是新課程的基本理念之一，學生的數學學習活動不應只限于接受、記憶、模仿和訓練.高中數學課程還應倡導自主探索、動手實踐、合作交流、閱讀自學等學習數學的方式.因此，探究式教學應成為數學課堂教學的主要方式之一，應該成為培養學生探究意識的主渠道、主陣地.課本習題是幾經編者篩選命制而成的，具有一定的代表性、典型性、探究性，是組織探究活動的有效載體，是培養學生探究意識的再生資源，值得教師重視.筆者選擇了蘇教版普通高中課程標準實驗教科書選修2-1中的一道習題，組織學生進行了一次有意義的探究活動.通過這次探究筆者感受到：用好課本習題對提高教學質量、培養學生的思維能力具有非常重要的意義.為行文方便，將原題附錄以下：

例1 過拋物線y2=2px(p＞0)的焦點的一條直線和拋物線有2個交點，且2個交點的縱坐標分別為 y1，y2，求證：y1y2=-p2.

從題目涉及的內容看，有直線方程、拋物線方程、方程組的解法，一元二次方程根與系數關系的應用，具有一定的綜合性，進行探究有助于溝通知識間的內在聯系，有利于優化知識結構;從動、靜的角度看，拋物線是相對靜止的，直線AB是運動的，進行探究有助于學生動中窺靜，靜中窺動;從原題給出的結論看：y1，y2是可變的，y1y2是不變的，進行探究有利于培養學生用運動、變化的觀點去思考問題;從原題的解決途徑看，有利于培養學生思維的靈活性與深刻性.

1 合作探究，尋覓多種解法

出示題目，讓學生思考、討論，教師巡視點撥，適時介入.當大部分學生基本完成本題解答時，教師請學生陳述解題思路.

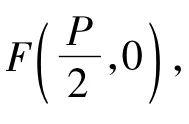
由韋達定理得

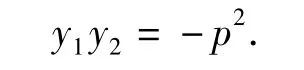
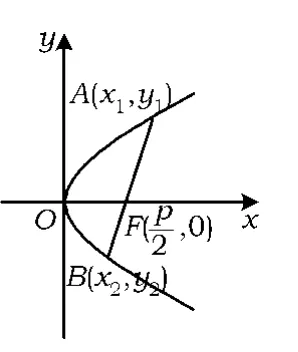
圖1

T1：S2的補充指出了部分學生解決這類問題的思維缺陷，今后用到含有斜率k的直線方程時應考慮斜率k不存在的情況.S1，你是怎么想到這一方法的?

S1：這是一道有關直線與拋物線位置關系問題，求證的結論是2個交點縱坐標之積為常數，這使我聯想到一元二次方程中的韋達定理.

T：S1根據直線與拋物線相交及題中結論呈現的形式聯想到一元二次方程根與系數的關系，是尋覓問題解決切入點的好辦法.此題還有別的解法嗎?

又因為y1≠y2，所以必有 y1y2=-p2.當 AB⊥x軸時，方法如S2所述.

綜合上述2種情況可知結論成立.

T：你是怎么想到這一方法的?

S：直線AB過焦點 F實際上隱含著點 A，F，B共線，利用斜率相等可構造方程.為了減少未知數的個數，利用點A，B在拋物線上，將2個點的橫坐標用含有y1，y2的式子表示，可簡化解題過程.

T：S3的思路有創意，對解題活動的開展很有啟發，利用已知條件減少未知量的個數，挖掘題目中隱含的條件構造方程.這體現了用方程思想解決問題的意識，拓寬了解題途徑.

S4：還可以用幾何知識解決.如圖2，過點A，B分別作拋物線準線l的垂線，垂足分別為A1，B1.因為AB過點F，由拋物線定義得|AA1|=|AF|，所以∠1=∠2.又 AA1∥FK，得∠1=∠3，從而∠2=∠3.同理可得∠4=∠5，因此∠A1FB1=90°.又由KF⊥A1B1，可得

T：你是怎么想到這一方法的?

S2：通過畫圖可以發現

圖2

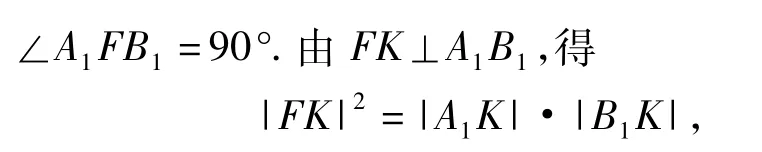
從而聯想到這種證法.

T：通過畫圖，直觀地發現要證的結論，這是幾何直觀給我們帶來的福音，它使我們容易看清問題的本質.S4的想法體現了數形轉換的思想，值得倡導.還有別的解法嗎?

由韋達定理得

T：此解法太妙了!S5避開了選擇斜率k為參數時對AB⊥x軸的討論，這啟發我們在選擇方法時，要盡可能地避開討論，減少失誤.

教學感悟學生的思維是活躍的，在課堂教學中如何讓學生打開思維的閘門，這就要求教師在課前對習題研究和在課堂上積極引導.優秀教師的功夫在課外，效率在課內.學生的成就感在于對問題的不斷解決，學生的快樂源泉在于不斷找到新方法.學生在愉悅的心境中思維效率最高，更容易催生學習的智慧.

2 選準入口，探求新型結論

通過一道課本習題，獲得4種解法(S1，S2的解法合一)，令人歡欣鼓舞.若就此收場，則實在有余味未盡之感.從原題的結論看，2個交點的縱坐標之積為定值，使人聯想：2個交點的橫坐標之積是否為定值?|AF|和|BF|之間又會有怎樣的關系?還會有其他什么結論?這些問題同樣值得思考.

T：從原題結論呈現的形式看，你能猜想出原題還可能會有什么結論?

S6：若原題中2個交點的橫坐標分別為x1，x2，則通過類比，可能有x1x2為定值.

T：你能猜出定值嗎?

將其代入y2=2px得

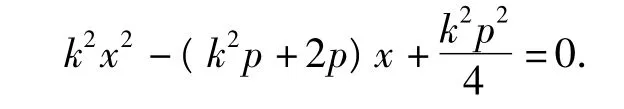
由韋達定理得

S8：當AB不垂直于 x軸時，由點 A，B，F共線可得

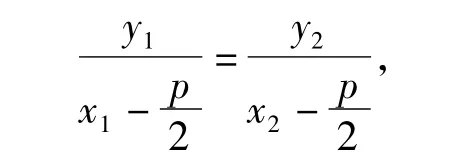
T：S6的解法具有通性，S7，S8的解法具有一定技巧，需要解題者有較強的洞察力.原題中|AF|，|BF|這2條線段值得關注，你能探索出這2條線段之間可能有什么關系嗎?

S10：這個直角梯形的兩底之和等于AB的長.

T：除此以外，還會想到什么樣的結論?

S10：以AB為直徑的圓與拋物線的準線相切.

T：你是怎樣想到的?

S10：在初中曾證過類似的幾何題.

T：好!你的發現實際上是拋物線過焦點的弦的又一條重要性質，請你說說證法.S10：如圖3，取AB的中點M，過點M作拋物線準線l的垂線交l于點 M1，則

圖3

因此以AB為直徑的圓與拋物線y=2px(p＞0)的準線相切(教室里發出一片贊嘆聲).

教學感悟學生蘊藏著一種巨大的智慧潛能.只要教師對問題的思考達到一定的深度，讓自己置身于學生之中，成為學生的合作者、“隱”導者、鼓勵者，學生就能從特殊到一般、從直觀到嚴謹，把新的認識上升到理性的、共性的高度，形成一般性結論.

3 變式探究，拓寬思維空間

一道以過拋物線焦點的弦為背景的習題可探究出多種解法和結論，如果把過焦點的弦變為過x軸上定點的弦，那么又會有什么結論?拋物線上的兩點滿足什么條件就能使這2個點連線經過拋物線焦點?這些問題同樣值得探究.

變式1 如果將原題條件中的“焦點”改為“定點 C(c，0)(c＞0)”，其余不變，那么 y1y2的值還是定值嗎?為什么?

有了對原題的探究基礎，學生對這個問題的求解已不陌生，很快有學生陳述了自己的解法.

根據韋達定理，得直時，由點 A，B，C 共線得

整理得

因為 y1≠y2，所以 y1y2=-2pc.

當AB⊥x軸時，方法同S11.

T：這2位同學的解法體現了一定的學習水平和研究水平，尤其是注意到了AB與x軸的關系，采用有效的方式來應對不同的情況，思路開闊、思維縝密.

變式2 如圖4，設 A，B為拋物線y2=2px(p＞0)上2個點，C為拋物線準線上的一點，點 A，O，C 共線，且 BC∥x軸.證明：直線AB恒過定點.

T：要證明直線AB恒過定點，我們能否猜出這一定點.

圖4

T：你是怎么發現的?

S13：通過特例計算得到AB過拋物線的焦點.

T：很好!滿足條件的直線AB恒過定點是一個具有一般性的結論，它必然包括特殊情況，S13用辨證的思想分析找到了目標.怎么證明，請把思路說一說.

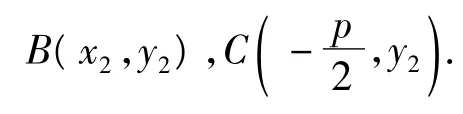
因此點A，O，C共線，且AC與x軸不垂直，于是則點M與點F重合，于是直線AB過定點F.

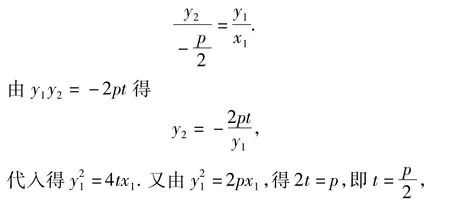
S14：設拋物線 y2=2px(p＞0)的焦點為 F，經過點F的直線交拋物線于點A，B，點C在拋物線的準線上，且BC∥x軸，證明：直線AC經過原點O(即證明點 A，O，C 共線).

S15：設拋物線 y2=2px(p＞0)的焦點為 F，經過點F的直線交拋物線于點A，B，延長AO到點C，交拋物線準線l于點C，證明：BC∥x軸.

T：S14，S15所編擬的2道題目與變式1是什么關系?結論成立嗎?

S14：這2道題是變式2的逆命題，其證明的思路應該與變式2相仿.

T：應該相仿，看來你還不能肯定，可以試一試.

S16：我已證出S14的結論，證明方法與變式2確實相仿.

T：好，同學們的思維非常靈活，由一道題又變出了2道新題，這既訓練了思維的靈活性，又使我們把握了這類問題的本質.同時，還告訴大家一個驚人的消息，S14所編擬的這道題就是2001年全國數學高考試卷中的解析幾何題(同學們驚訝不已!頓時教室里響起了熱烈的掌聲).

教學感悟解題教學不能忙于“趕路”，弄透一題，勝于教完十題.只有走進題目的“心靈深處”，才能欣賞數學的“多彩世界”.

4 橫向聯系，提升綜合能力

在不同的知識背景下，運用所學知識分析并解決問題是對學生學習能力的檢驗.因此，培養學生探索、提取、應用知識的能力，方能為問題的探究提供有力的智力保障.

如果把變式2以向量的形式呈現，那么可衍生出如下題目：

(1)當t變化時，求點B的軌跡n;

T：看到這道題目后，首先想到了什么?

T：你能說說求點B軌跡方程的思路嗎?

由式(1)，式(2)消去t得

所以點B的軌跡為以原點為頂點，焦點在x軸正半軸上的拋物線.

T：這是一道求動點軌跡的題目，而條件是通過向量形式表現出來的.如何實現向量條件的轉化，是解決這道題目的關鍵.S16較好地把握了這一關鍵，值得大家學習.

教學感悟 將原題的條件換一種方式呈現，尤如讓學生“在不同地方見到同一個人”，有利于知識的溝通，強化知識間的內在聯系.

5 精選習題，有效開發資源

課本是教學之本、教學之源，同樣課本也應成為課堂教學的探究之本、探究之源.課本上有許多適于探究的鮮活材料，作為教師必須以睿智的目光發現適于探究的素材，并進行有效開發.

5.1 選題要具有典型性

課本上的很多習題都具有一定的代表性，它的價值在于基礎性和可探究性.只有選取這樣的習題，才能構建基礎性訓練和探究性訓練的思維體系，才能使探究活動有一個基本保障.離開了這個保障，探究活動就不能有效地開展下去;離開了這個保障，學生的學習興趣和積極性就不能有效調動.因此，精心選題是保證全員參與的前提，也是保證整體教學效益的前提.

5.2 問題的設計要有層次性

5.3 探究過程要注重學法指導