基于定數(shù)截尾數(shù)據(jù)指數(shù)分布參數(shù)的最短區(qū)間估計(jì)

王玉芳

（荊楚理工學(xué)院 數(shù)理學(xué)院，湖北 荊門(mén) 448000）

基于定數(shù)截尾數(shù)據(jù)指數(shù)分布參數(shù)的最短區(qū)間估計(jì)

王玉芳

（荊楚理工學(xué)院 數(shù)理學(xué)院，湖北 荊門(mén) 448000）

根據(jù)定數(shù)截尾數(shù)據(jù)，給出了參數(shù)的常用區(qū)間估計(jì)和最短區(qū)間估計(jì)，另外，還介紹了最短區(qū)間估計(jì)的求法。

定數(shù)截尾數(shù)據(jù)；指數(shù)分布；最短區(qū)間估計(jì)

1 引言

指數(shù)分布是壽命試驗(yàn)中常見(jiàn)的分布之一，其重要性首先在于，現(xiàn)實(shí)中許多樣本的壽命都服從指數(shù)分布；其次，由于它的參數(shù)的點(diǎn)估計(jì)和區(qū)間估計(jì)易于得到，并且由指數(shù)分布可以派生出Γ分布、x2分布、F分布，這些分布的統(tǒng)計(jì)理論較為成熟。本文首先給出定數(shù)截尾試驗(yàn)下人們較為熟悉的關(guān)于參數(shù)的區(qū)間估計(jì)，最后討論了最短區(qū)間估計(jì)問(wèn)題。

2 參數(shù)的極大似然估計(jì)和區(qū)間估計(jì)

設(shè)總體T服從參數(shù)為λ的指數(shù)分布，其密度函數(shù)為：

從服從該指數(shù)分布的一批產(chǎn)品中任取n個(gè)產(chǎn)品進(jìn)行壽命試驗(yàn)，試驗(yàn)進(jìn)行到事先規(guī)定的失效數(shù)時(shí)停止r(r≥），設(shè)其先后失效時(shí)間為t1≤t2≤…≤tr，其余n-r個(gè)在試驗(yàn)停止時(shí)刻tr尚未失效，由此所得到的就是定數(shù)截尾樣本。

由此試驗(yàn)可得如下引理:

引理1：設(shè)t1,t2,…,tr是由n個(gè)試驗(yàn)樣品的截尾數(shù)為r的定數(shù)截尾樣本，則總試驗(yàn)時(shí)間T*r=t1+…+tr+(n-r)tr服從Γ （r,λ）分布，即T*r的概率密度函數(shù)為：

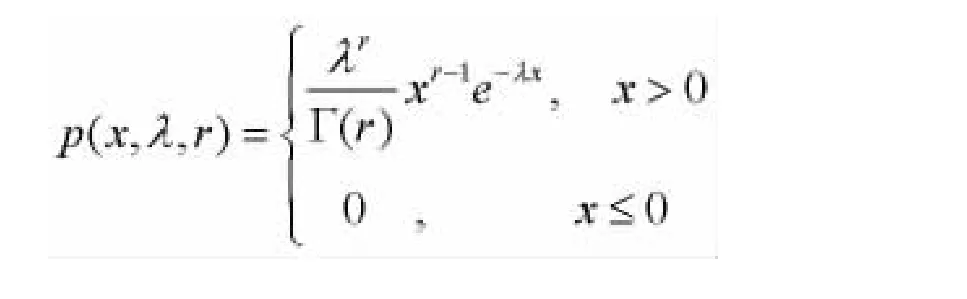
由引理1可得

引理2：隨機(jī)變量2λT*r 服從自由度為2r的x2分布，即有2λ(2r)由引理2可得到2λ的概率密度函數(shù)為

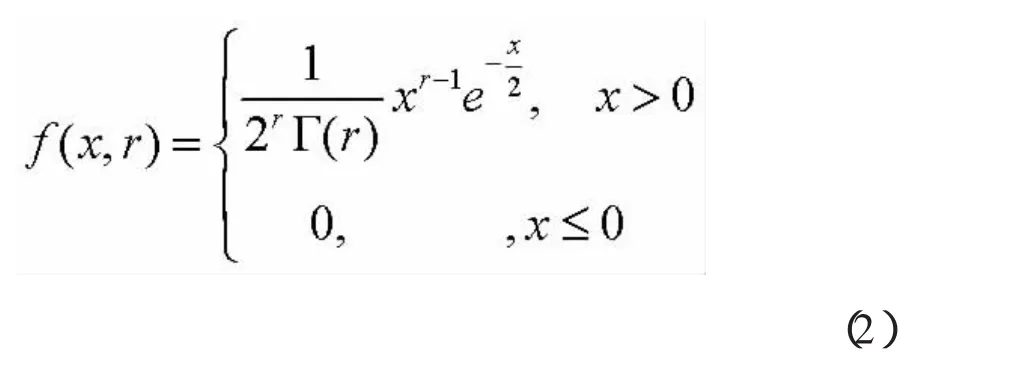
引理1和引理2的證明見(jiàn)文獻(xiàn) ［1］。

因此，由引理2對(duì)于給定的顯著性水平α∈ （0，1），

由此可得

在產(chǎn)品的壽命服從指數(shù)分布 （1）的定數(shù)截尾試驗(yàn)中，參數(shù)λ的置信度為1－α的置信區(qū)間為

推論 關(guān)于參數(shù)λ的統(tǒng)計(jì)假設(shè)檢驗(yàn)問(wèn)題：

原假設(shè) H0∶λ＝λ0，備擇假設(shè) H1∶λ≠λ0，

其中，λ0是某事先給定的常數(shù)。取統(tǒng)計(jì)量T＝2λ0T*r，則在給定的顯著性水平α∈ （0，1） 下，當(dāng)時(shí)，接收原假設(shè)時(shí)，拒絕原假設(shè)H0而接受備擇假設(shè)H1。

由于x2分布的分位數(shù)有專用的x2分布表可查，使用起來(lái)比較方便，因此 （3）也是λ的常用區(qū)間估計(jì)，但是 （3）并不是λ的最短區(qū)間估計(jì)，下面將討論λ的最短區(qū)間估計(jì)問(wèn)題。

3 最短區(qū)間估計(jì)

對(duì)指數(shù)分布的參數(shù)λ作區(qū)間估計(jì)時(shí)，在固定的置信度下，我們一般認(rèn)為置信區(qū)間越短越好。對(duì)于第二節(jié)推導(dǎo)出的λ的區(qū)間估計(jì)，由于隨機(jī)變量2λ服從x2(2r)分布，它的密度函數(shù) （2）不是關(guān)于峰值對(duì)稱，所得到的置信區(qū)間

對(duì)給定的置信度1－α，設(shè)x1x2滿足下式 不是最短的。

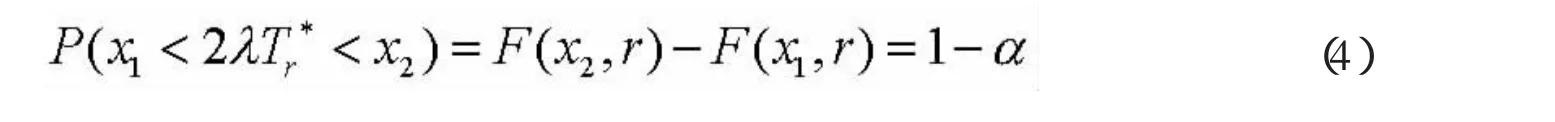
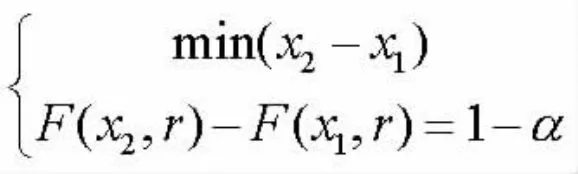
要解決上述條件極值問(wèn)題，其顯示解很難得到，因此我們先證明該條件極值的駐點(diǎn)是唯一存在的。

命題：當(dāng)r≥2時(shí)，上述條件極值有唯一駐點(diǎn)。

證明：由拉格朗日乘子法，令

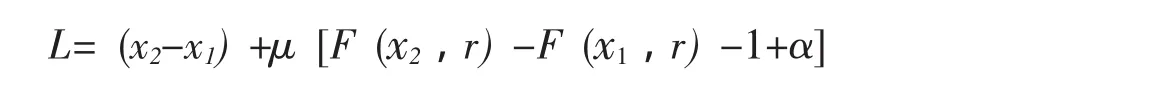
對(duì)x1，x2求偏導(dǎo)且令偏導(dǎo)為零，得

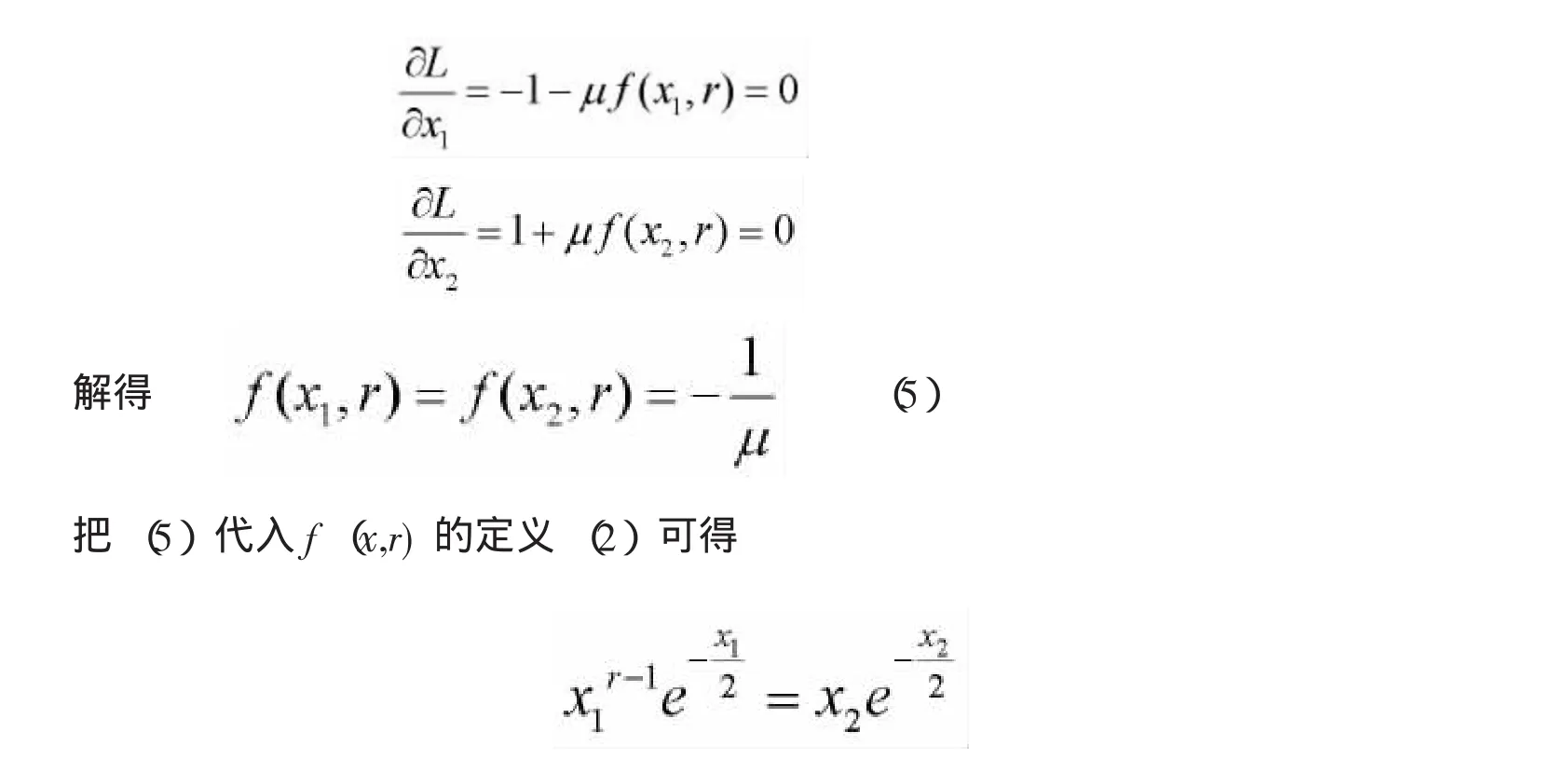
所求駐點(diǎn) (x1-x2)就是（4）式與（6）式的解。這樣，僅需證明（4）式與（6）式有解而且解是唯一的。令

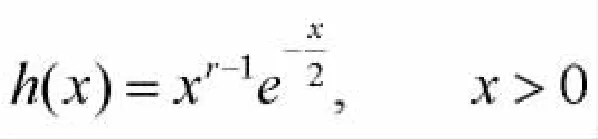
由 h′(x)=0，可得唯一穩(wěn)定點(diǎn) x0=2r-2；且當(dāng) x≤x0時(shí)，h′(x)≥0,h(x)嚴(yán)格單調(diào)遞增，當(dāng) x≥x0時(shí)，h′(x)≤0,h(x)嚴(yán)格單調(diào)遞減，因此x0=2r-2是h(x)的最大值點(diǎn)；而當(dāng)x趨于正無(wú)窮大或零時(shí)h(x)趨于零。為保證x1＜x2和（6）式成立，應(yīng)有 x1＜2r-2，x2＞2r-2。這樣由任意 x2可唯一地解出 x1=u(x2)。

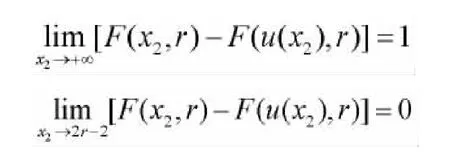
對(duì)于r≥2時(shí)，最短置信區(qū)間的求法可用MATLAB軟件求得。

由區(qū)間估計(jì)和假設(shè)檢驗(yàn)的關(guān)系，根據(jù)最短區(qū)間估計(jì)也可類(lèi)似上述推論給出雙邊假設(shè)檢驗(yàn)問(wèn)題，這里不再列出。

[1]勞立斯（Lawless.J.F）.壽命數(shù)據(jù)中的統(tǒng)計(jì)模型與方法[M].茆詩(shī)松，譯.北京：中國(guó)統(tǒng)計(jì)出版社，1998.

[2]茆詩(shī)松，王靜龍，濮曉龍.高等數(shù)理統(tǒng)計(jì)[M].北京：高等教育出版社，1997.

[3]顧嘉麟，郭建英.截尾數(shù)據(jù)下威布爾分布的參數(shù)估計(jì)問(wèn)題[J].哈爾濱理工大學(xué)學(xué)報(bào)，2005，10（2）：61-63.

[4]茆詩(shī)松，王玲玲.可靠性統(tǒng)計(jì)[M].上海：華東師范大學(xué)出版社，1984.

O212.2

A

1673-8535(2010)03-0015-04

王玉芳 (1976-)，女，湖北天門(mén)市人，荊楚理工學(xué)院數(shù)理學(xué)院講師，碩士研究生，研究方向：概率統(tǒng)計(jì)。

（責(zé)任編輯：鐘世華）

2009-10-22