質量成本與質量水平關系及其模型研究

尚珊珊，尤建新

（同濟大學 經濟與管理學院，上海 200092）

0 引言

質量成本由預防成本、鑒定成本以及損失成本組成，即PAF模型。質量成本花費的多少一定程度上可以反映出質量水平的高低，因此了解質量成本與質量水平間的關系，有利于為決策者提供決策建議，方便決策者做出正確的結論。質量成本與質量水平間的關系主要有以下三種模型如圖1,2,3所示。

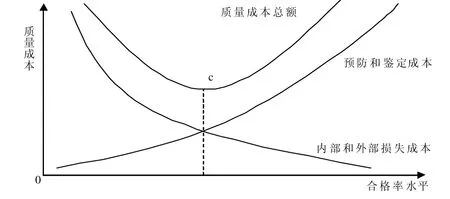
圖1 Feigenbaum質量模型圖

圖2 Juran質量成本模型圖

1 質量成本與質量水平的理論關系分析

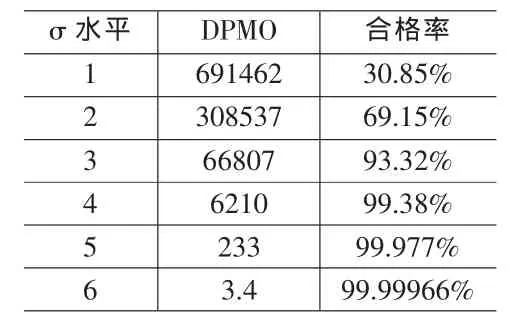
表1 σ與質量改進效率

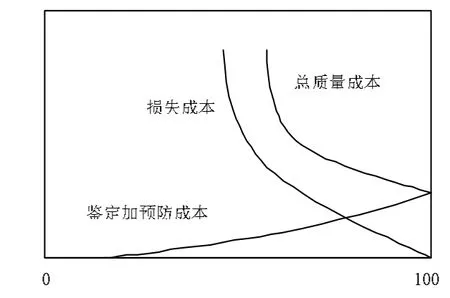
圖3 新最佳質量成本模型

質量水平，即質量一致性，通常用合格率來表示。這里采用6σ管理中的σ水平來衡量。σ水平反映了質量改進獲得實際結果與其目標之間的差距或偏離程度。σ越大說明偏離或波動程度越大，質量改進的效果越差，而σ越小，則表明質量改進的效果越好，因此，質量改進的效率可用不同的σ水平來描述。分別用缺陷率或合格率作為質量改進效率的衡量標準，σ水平與其之間的關系如表1所示，其中DPMPO為每萬次機會的缺陷數

從圖2,3可以看出Feigenbaum與Juran的質量模型的思想是一致的，只是Feigenbaum更進一步細化了圖形。

1.1 基于指數函數模型的最佳質量成本水平

用負指數函數表示質量損失成本,式(1)所示;用指數函數表示質量保證成本,式(2)所示。

所以,質量成本數學模型為：

式中:a1—控制廢次品趨于0時,所發生的最小次品損失費用;

b1—追加成本費用的增長率,即指數函數的斜參數;

a2—控制合格率趨于100%(廢次品趨于0)時,生的最大成本費用;

b2—控制成本費用的增長率,即指數函數的斜參數;

Q—產品合格率。

從式（4）可以計算出最佳質量水平時的合格率，然后可以根據表可以得出最佳σ水平。

1.2 基于田口模型的最佳質量成本水平

根據田口玄一的質量成本模型：

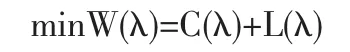
質量損失函數 L(λ)=a1+b1(λ-1)2

質量保證成本函數 C(λ)=a2λb2

所以,質量成本數學模型為：

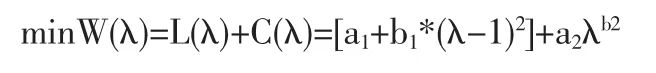
式中:λ是質量水平即產品的合格率;a1是企業的全部產品達到完全合格時仍造成的損失 (如能源消耗污染等),a1的值可根據企業近5年來在治理污染噪音等方面投資的加權平均值求得;b1=L″(1)/2;a2={A[α/(α+β)]α·[β/(α+β)]β}-1/(α+β);b2=1/(α+β)

1.3 基于K.K.Govil模型的最佳質量水平

利用K.K.Govil函數表達質量成本數學模型，式 (5)所示。通過對(5)式的微分、回歸分析,確定具體質量成本模型的K,F,G,R值,通過層次分析法(AHP),使質量水平和質量成本處于理想控制狀態。

設K為每件廢品造成的損失,Q為合格率,(1-Q)為不合格率。則每件合格品負擔的損失費用是C1=K[Q/(1-Q)]R。每件產品的預防檢驗費用C2=F[(1-Q)/Q]G,F是C2隨不合格率與合格率的比值而變化的系數。

式中:K、F、R、G＞0 且為常數。

最佳質量水平:Q=1/[1+(KR/FG)]1/(R-G)

由于近年來隨著質量水平的提升，質量合格率的增高，質量成本預防成本、鑒定成本、損失成本以及總成本都會隨之變化，總質量成本隨著質量水平的提高而降低，損失成本隨著質量成本的提高而降低。如圖4所示：選擇。首先可以根據不多的質量成本與質量水平歷史數據，分析它們之間的灰色關聯度，從而可以根據灰色關聯度大概判斷質量成本與質量水平間的關系。

首先，收集質量成本以及質量水平歷史數據，并根據歷史數據作出他們的曲線圖，從曲線圖中先直觀的查看它們之間的關系，例如：

質量成本的歷史數據序列為：C=（1.8，1.5，1.4，1.2，1，0.8），質量水平的歷史數據序列為：P=（0.8，0.83，0.87，0.9，0.94，0.96）

圖4 不同質量水平下的總質量成本

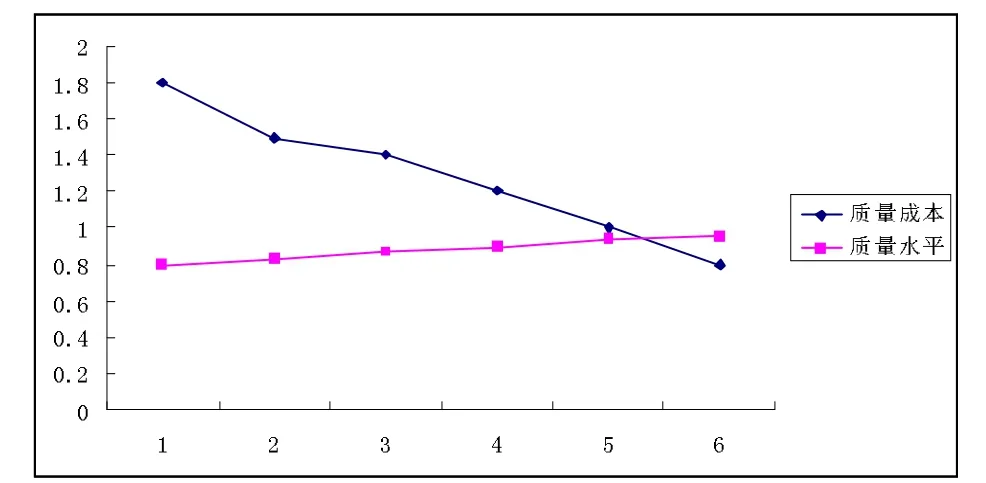
圖5 質量成本與質量水平曲線圖

從圖5中，可以初步判斷質量成本與質量水平存在負相關關系，隨著質量水平的提高，質量成本是逐漸降低的。

然后，我們可以根據灰色相關理論根據歷史數據具體計算出質量成本與質量水平間的灰色關聯度。

定義 1 設 Xi=（xi（1），xi（2），…，xi（n））為因素 Xi的行為序列，D1為行為序列算子且：

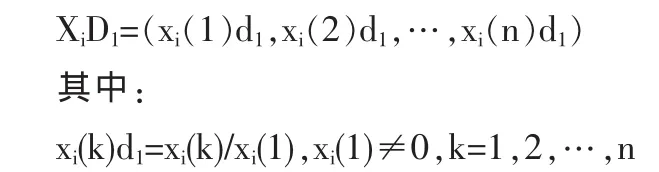
則稱D1為初值化算子，XiD1為Xi在初值化算子D1下的像，簡稱初值像。

定義 2 設 Xi=（xi（1），xi（2），…，xi（n））為因素 Xi的行為序列，D2為行為序列算子且：

2 質量成本與質量水平的灰色相關關系分析

根據以上討論，可以看出，在理論情況下我們可以采用不同的質量成本模型從而計算出最佳的質量水平，但是實際應用當中，完全依據理論上的模型很難計算出。而且，實際過程中經常沒有非常多的質量成本和質量水平數據用以做一般的數據統計分析，因此，采用灰色系統進行分析是不錯的

則稱D2為均值化算子，XiD1為Xi在均值化算子D2下的像，簡稱均值像。

初值化算子D1和均值化算子D2皆可使系統行為序列無量綱化，且在數量上歸一，在進行系統分析時，可根據情況選用一種。

定義 3 設 X0=（x0（1），x0(2)，…，x0（n））為系統行為特征序列且：

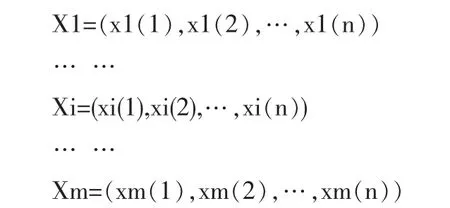
為相關因素序列。給定實數γ(x0(k),xi(k))，若實數：

滿足：

則稱 γ(X0,Xi)為 Xi與 X0的灰色關聯度，γ(x0(k),xi(k))為 Xi與X0在k點的關聯系數，并稱條件(1)～(4)為灰色關聯四公理。

因此，根據以上定理可以計算質量成本和質量水平間的灰色相關系數，其步驟如下：

第一步，收集質量成本及質量水平歷史數據，設質量成本和質量水平每組各共n個歷史數據，令質量成本、質量水平的序列為X0，X1，求這兩個序列的初值像或均值像Xi’（i=0，1），即：

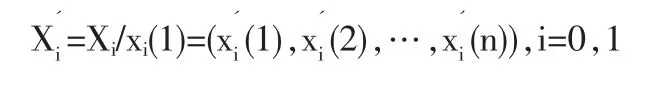
第二步，求差序列。記：

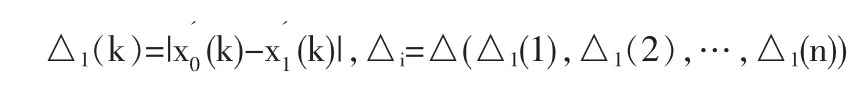
第三步，求兩級最大差和最小差。記為：

第四步，求質量成本和質量水平各元素間的關聯系數：

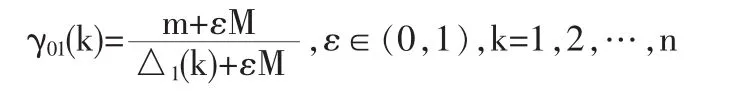
第五步，計算質量成本和質量水平整體間的關聯度：

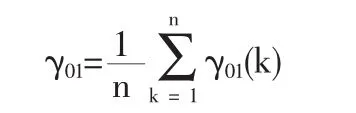
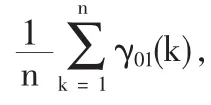
3 質量成本與質量水平的灰色線性回歸組合模型建立

為進一步研究質量成本與質量水平間的關系，我們可以建立質量成本與質量水平間關系的研究模型，可以看出，質量成本與質量水平間不僅存在指數關系，而且也存在先行關系，因此，采用灰色線性回歸模型可以改善原線性回歸模型中沒有指數增長趨勢和灰色GM（1，1）模型中沒有線性因素的不足，因此該組合模型更適合于既有先行趨勢又有指數增長趨勢的序列。

以往的質量成本與質量水平的研究中往往采用的是指數模型，而忽略掉線性關系部分，因此，這次我們采用灰色線性回歸模型，從而可以考慮到指數模型與線性模型兩部分。

設質量成本序列為X(0)

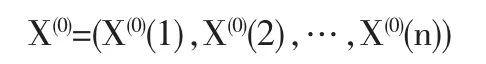
對X(0)進行一次累加省內成處理，得到生成序列為：

由 GM（1，1）可得到：

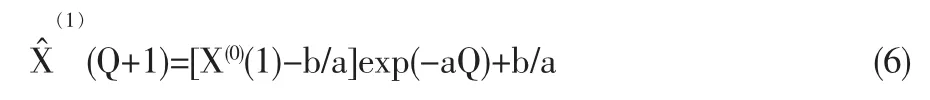
其形式可記為：

對于質量成本與質量水平間的關系模型，采用線性回歸Y=aX+b及指數方程Y=a·exp(X)的和來擬合累加生成序列，其中，v，C1，2 為參數。

現在需要確定v，C1，C2參數的值。為了確定參數值，首先設參數序列：

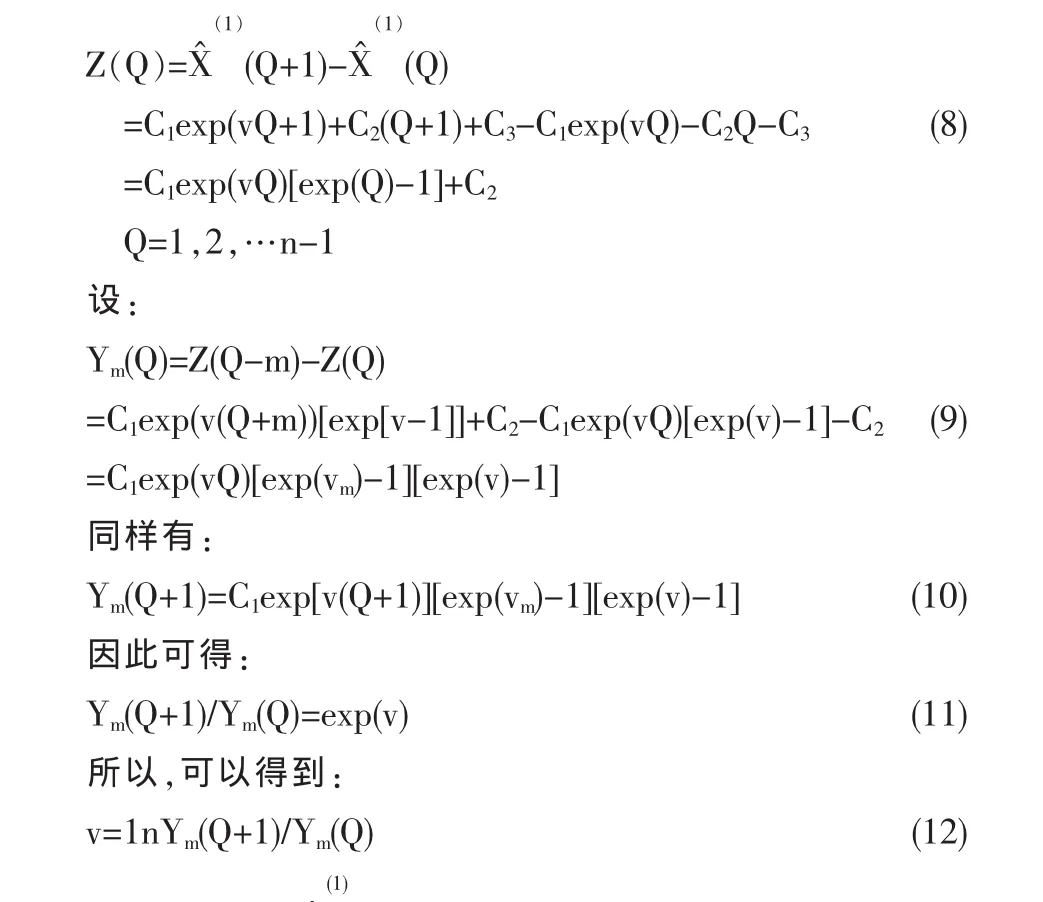
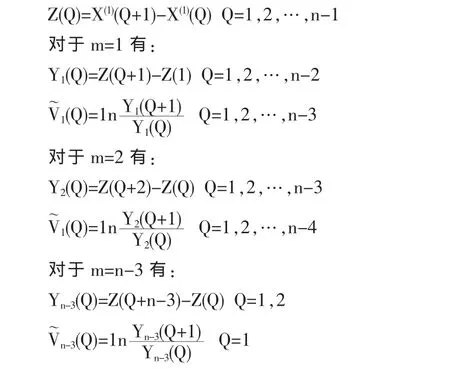
利用最小二乘法可求得C1，C2，C3的估計值。令：

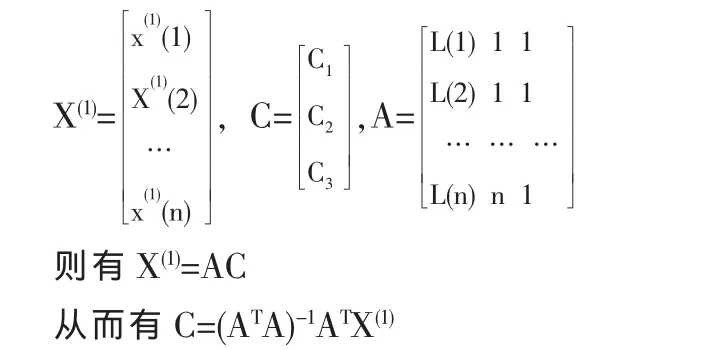
這樣根據數據歷史值可以生成質量成本與質量水平間的關系模型為：

從式(14)可以看出，如果C1等于0，則一次累加生成序列為線性回歸模型，如果C2等于0，則累加生成的序列為GM(1，1)模型。該模型使線性回歸模型中不含指數增長趨勢及GM(1，1)模型中不含線性因素的情形有所改善。

4 結論

如今越來越多的企業關注質量成本，而質量成本與質量水平有著密切的關系，以往的理論中往往只是對質量成本與質量水平間的理論研究，而并沒有切實考慮到實際應用當中所遇到的種種問題，因此本文在考慮實踐中歷史數據經常不會足夠多，所以采用了利用灰色系統理論來分析質量成本與質量水平間的關系。而且，通常以往文獻中的質量成本模型的理論研究中往往只考慮到指數部分的影響，本文則采用了灰色系統與線性回歸相結合的組合模型方式來建立質量成本與質量水平的關系模型，從而能夠有效改善以往系統中沒有考慮到線性部分，建立更為切實準確的模型。

[1]Abed,M.H.,Dale,B.G.Quality Assurance[M].Englang:Gower Publishing Limited，1987.

[2]Albright,T.L.,Roth,H.P.The Measurement of Quality Costs:an Alternative Paradigm[J].Accounting Horizons，1992,（6）.

[3]Kulkarni,S.Prybutok,Process Investment and Loss Functions:Models and Analysis[J].European Journal of Operational Research，2004,157(1).

[4]Kulkarni,S.S.Loss-based Quality Costs and Inventory Planning:General Models and Insights[J].European Journal of Operational Research，2007,188(2).

[5]梁淑明,張根保.質量成本與西格瑪能力之關系模型探討[J].管理技術，2006,(5).

[6]王華.最佳質量成本決策方法[J].商業經濟，2004,(5).

[7]劉東才,雒征,張文華.最佳質量成本模型的研究[J].武漢理工大學學報，2007,（5）.

[8]白寶光,張世英.質量成本模型及其優[J].科學管理研究，2005,（23）.

[9]汪邦軍.質量成本曲線方程與質量改進的經濟分析[J].北京機械學院學報,2002,(2).