角度平均方向-合向量長度θˉ-R控制圖模擬
楊 昆,吳東旭
(遼寧工程技術大學 安全科學與工程學院,遼寧 阜新 123000)
0 引言
在閉域圓中,某些質量特性值常以角度形式出現,并且總體服從Von Mises分布,在這種質量控制情形下,顯然以開域為前提的傳統控制圖不能適應,方英等[1]將控制圖和方向數據統計這兩個方面相結合,將方向數據統計用于控制圖,設計了計角值控制圖,從而完善了控制圖體系。較為常用的是基于均勻數值進行的過程控制,如何盡快發現和判斷生產的異常,成為研究計角值控制圖性能的一個重要指標。該文充分借鑒了常規控制圖性能分析的研究思路,并結合圓上閉域的特點,運用統計控制過程中的重要工具平均鏈長(the average run length)對角度平均方向-合向量長度控制圖的性能進行了蒙特卡洛模擬分析。

1.1 控制圖的建立
假定質量特性值服從Von Mises分布M(μ0,k),R是樣本合向量長度,R控制圖主要用于觀察分布的離散情況或變異程度的變化。
設P(R≤Rα),則R的控制界限為
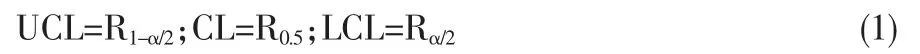
根據組內樣本量n,計算P(r,n)。給出了n=3,4,5時的P(r,n)分布的R分位點。
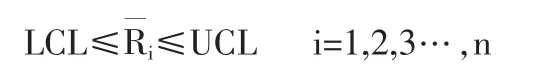
質量特性值服從 Von Mises 分布 M(μ0,k),是樣本平均合向量方向,平均方向控制圖是利用質量特性數據的平均方向來反映和控制質量數據集中位置的變化。
根據抽樣得到的質量特性值來計算控制界限如下
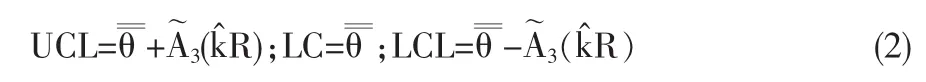
計算θˉ控制圖的控制界限應從R控制圖開始,因為θˉ的控制界限中包含R,若R控制圖未判穩,則過程的變異度失控,計算出來的控制界限就沒有多大意義。
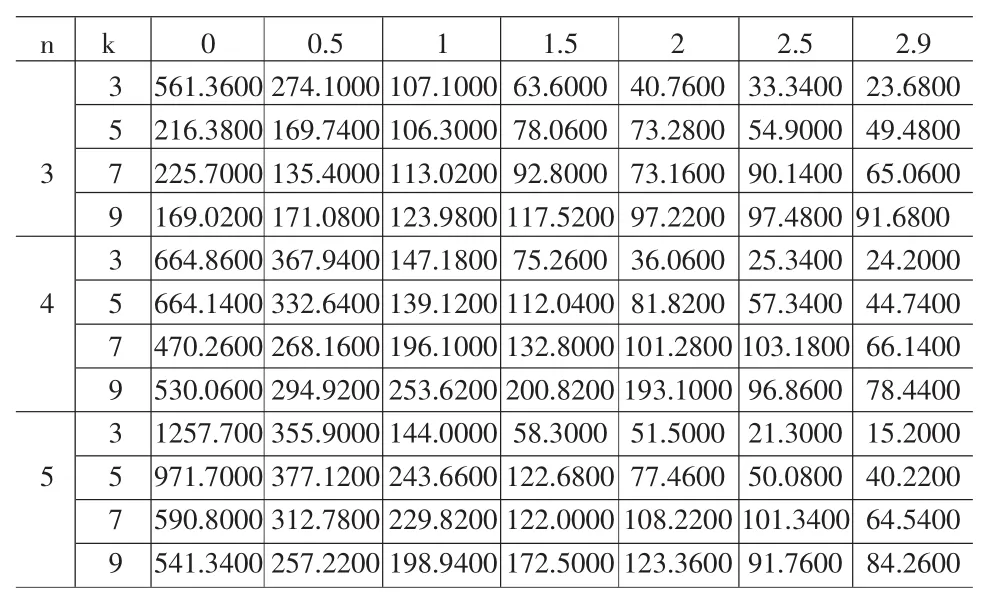
表1 α=0.001時,k偏移0-2.9的ARL
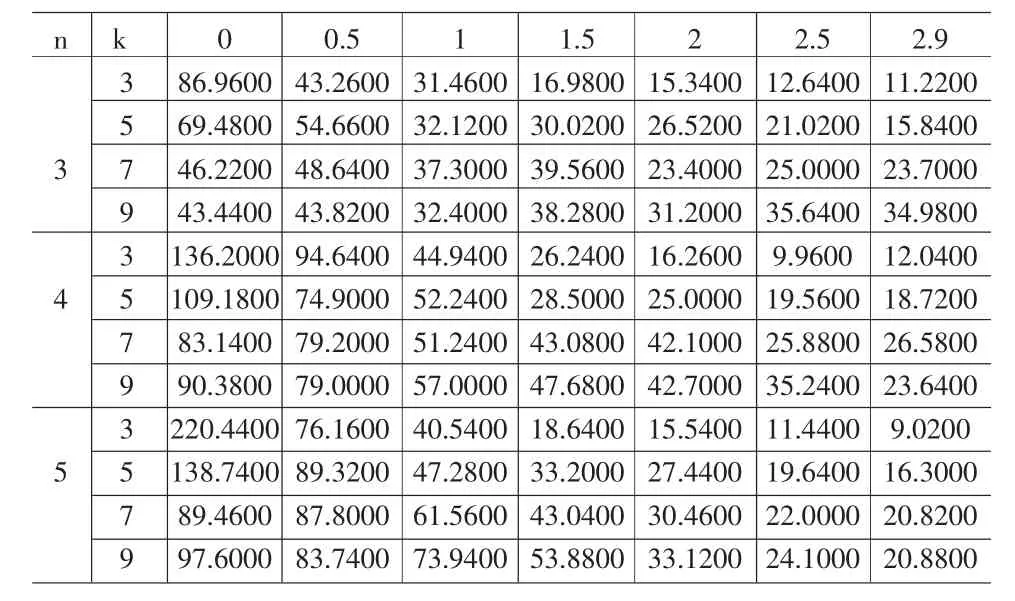
表2 α=0.005時,k偏移0-2.9的ARL
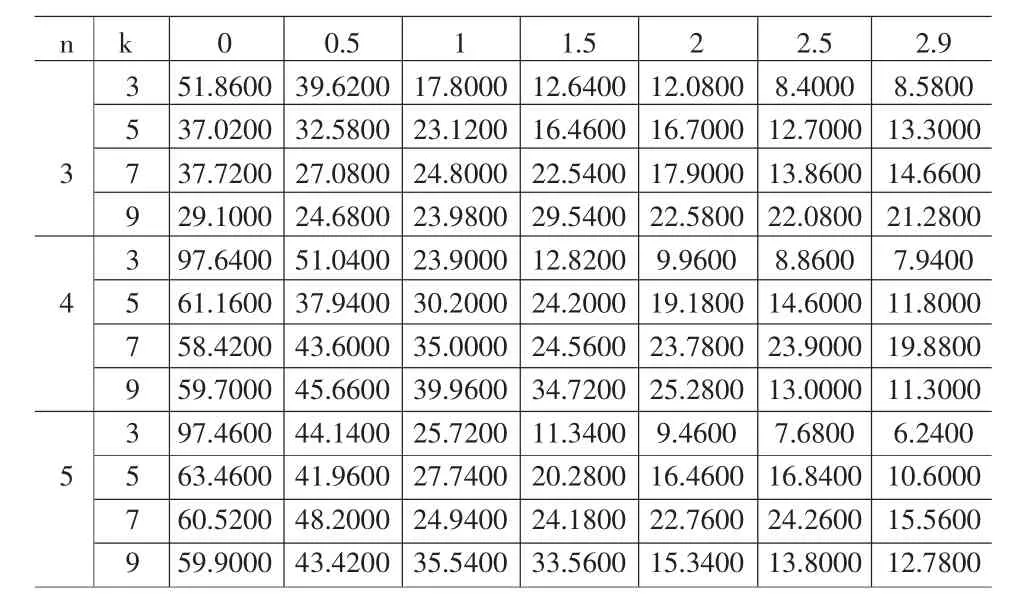
表3 α=0.01時,k偏移0-2.9的ARL
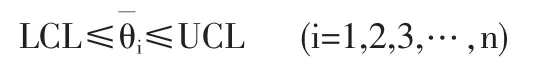
同樣對控制圖的重要指標-平均鏈長ARL進行模擬。在過程處于統計控制狀態時,ARL越長,控制圖的效果越好;當過程未處于統計控制狀態時,ARL越短,控制圖的效果越好。本文采用Monte Carlo模擬[4]方法得到平均方向-合向量長度θˉ—R控制圖的平均鏈長ARL。
2.1 控制圖模擬
考察在α=0.001、α=0.005和α=0.01三種不同控制狀態下,當k發生偏移時,組內樣本量取何值更能有效的使控制圖對過程發生異常的情況下作出更加快速的反映。這里取k=3,5,7,9取作為研究對象,使原始數據的k值偏移0-2.9,觀察所對應的平均鏈長ARL的變化。表1~3分別對應當α=0.001、α=0.005和 α=0.01時,k偏移 0-2.9的平均鏈長值ARL;
從表1~3可以得出如下結論:
(1)在α和k值相同的情況下,隨著k的偏移,無論組內樣本量n為何值,ARL都呈現遞減趨勢。
(2)在α和k值相同的情況下,隨著k的偏移,隨著組內樣本量n的增加,ARL呈現遞減趨勢更加明顯,這說明組內個數的取值對較快查出控制圖發生異常是有一定作用的。從表縱向數據可以看出組內樣本量n=5時,在未發生偏移的情況下,ARL5最長,而發生偏移之后ARL5遞減速度最快。因此,組內樣本量取n=5時能更好的反映合向量長度控制圖的性能。n=3時的效果最差。n=4時的效果與n=5時的效果接近。
(3)隨著α值的增加,虛發報警概率在增大,漏發報警概率在減小,由ARL的遞減速率可知漏發報警概率對ARL的作用要大于虛發報警概率,這對控制圖檢出異常因素是不利的。
(4)在α值相同的情況下,隨著k的增加,未發生偏移的ARL在逐漸減小,當k=3時,ARL值最高且最接近1/α。從表中也可以看出這個規律。發生偏移的ARL的斜率也在逐漸減小。
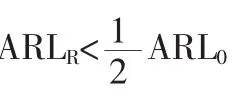
2.2 平均方向控制圖模擬
每次取樣本量為100000,組間樣本量為5,重復50次,在不同α狀態下,考察隨均值μ發生偏移時的平均方向θˉ控制 圖 的 平 均 鏈 長 ARL值 。 其 中 取 K=3,5,7,9, 在 α=0.001,0.005,0.01情況下,對均值發生偏移角度分別為5度、10度、15度、20度、25度、30度、35度、40度、45度、50度。隨均值μ發生偏移時的平均方向θˉ控制圖的平均鏈長ARL值見表4所示。
從表4可以得出如下結論:
(2)在相同的α值下,當中心發生偏移的時候,k越大,平均方向控制圖的平均鏈長ARLˉ值遞減的速率越快。
θ
θ異常的速度比較快。
3 結論
本章運用蒙特卡羅方法對計角值控制圖中占有重要地位的角度平均方向-合向量長度θˉ-R控制圖的重要指標平均鏈長ARL進行了模擬研究,并模擬了在對角度平均方向和合向量長度進行偏移處理之后對平均鏈長的影響。在對θˉ-R控制圖選取樣本點之后,取組內樣本量為何值才是合理子組進行了模擬比較,分析結果顯示當n=5時平均方向控制圖的控制效果最好。
[1]方英,李元生.角度平均方向-合向量長度控制圖[J].清華大學學報(自然科學版),2006,46(3).
[2]Kanti V.Mardia,Peter E.Jupp.Directional Statistics[M].London:Academic Press Inc,1972.
[3]楊昆.計角值控制圖的模擬與過程能力分析[D].北京:中國礦業大學(北京),2008,1.
[4]徐鐘濟.蒙特卡羅方法[M].上海:上海科學技術出版社,1985.

