上海金屬期貨與現貨市場非對稱波動溢出效應的實證研究

陳 鋒，高展軍

（西北政法大學 經濟管理學院，西安 710063）

上海金屬期貨與現貨市場非對稱波動溢出效應的實證研究

陳 鋒，高展軍

（西北政法大學 經濟管理學院，西安 710063）

運用二維非對稱BEKK-GARCH模型，考察了上海金融期貨與現貨市場間收益率的非對稱波動溢出效應。實證結果表明：樣本期鋁期貨與現貨收益率間存在雙向的波動溢出效應，而銅期貨與現貨收益率波動溢出效應不顯著；銅、鋁期貨、現貨市場間都存在雙向的波動非對稱效應，都對來自對方市場的“消息”的沖擊有顯著的反應。

波動溢出效應、波動非對稱性、向量GARCH模型

1 研究方法

金融研究與實務領域，無疑更關注兩市場之間收益率條件均值的變動和相互作用，這也是本文研究的主要目的，因此需要建立多元GARCH模型來考察市場間波動溢出效應。

Kraft，Engle(1983)提出了向量ARCH類模型，設一個維向量隨機序列：

在式（1）中，Mt為其均值向量，{εt}是一個 N×1 維向量隨機序列，且有εt|It-1～N(0,Ht),It-1是到t-1時刻的信息集，Ht是N×N維正定矩陣，且關于It-1是可測的。定義ht=Vech(Ht)，Vech（·）稱為向量半算子，表示把矩陣Ht的下三角陣按列依次堆積而成的N(N+1)/2維向量，向量GARCH類模型主要是研究Ht的不同動態特性。

此后，Bollerslev，Engle 和 Wooldridge（1988）提出擴展的向量GARCH模型中Vech(Ht)形式表示為：

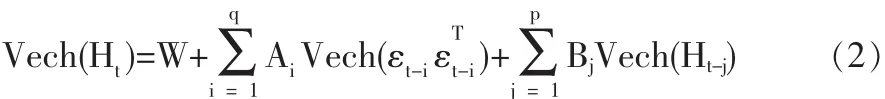
其中，W為N(N+1)/2維向量，Ai和 Bj均為[N(N+1)/2維方陣，且 Ai和 Bj使 Ht正定，i=1,2,3…p,j=1,2,3…q。

向量GARCH模型非常適合分析多市場之間的波動溢出效應，模型參數矩陣Ai和Bj中的對角線元素反映方差、協方差序列自身的相關關系；而非對角線元素反映了不同變量的方差、協方差序列之間的相互影響，但向量GARCH模型的缺點參數過多，估計比較困難，而且實際運用中很難保證Ht正定。

Engle 和 Kroner(1995)在綜合 Baba，Engle，Kraft和 Kroner的研究基礎上提出了一種實施正定限制的參數化模型，簡稱為BEKK-GARCH模型，其模型表示如下：

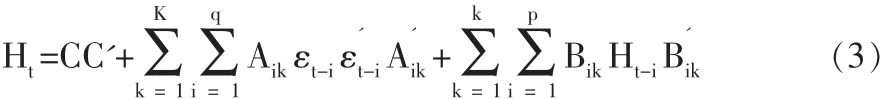
式（3）中，Aik和 Bik為 N 維方陣，C 是[N(N+1)/2]的上三角陣，當K=P=q=1，簡化的BEKK-GARCH(1,1)模型可以表示為式（4）：

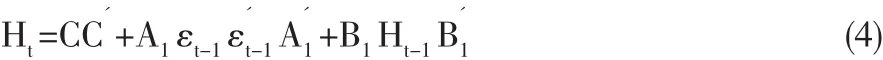
BEKK-GARCH模型的優點是容易滿足Ht的正定，待估計的參數也相對較少，但模型中參數的經濟學涵義相比于向量GARCH模型不夠明確。在式(4)BEKK模型中往往假設殘差項εt服從多元正態分布，而現實中金融時間序列往往呈現“尖峰厚尾”的特征，并不能完全服從正態分布，t分布或廣義誤差分布（GED）相比正態分布能更好的反映序列的“尖峰厚尾”的特征。

Kroner和Ng(1998)在BEKK-GARCH模型的基礎上，提出包含一般動態協方差的非對稱BEKK模型（Asymmetric BEKK）。 令 ηit=max[0,-εit]和 ηt=[η1t…ηNt]，則非對稱 BEKK 模型可以被定義為式（5）的形式：

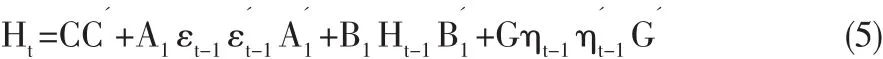
其中，G為N維方陣，且ηit為負值，代表了壞消息對Ht產生的沖擊影響，只需G方陣中所有元素顯著不為0，就說明存在著非對稱的杠桿效應。

國外文獻中BEKK-GARCH模型的運用主要有：Karolyi(1995)使用BEKK-GARCH模型估計了美國和加拿大股票市場收益率間的波動關系；Kearney and Patton(2000)運用BEKK-GARCH模型分別估計了三個、四個和五個匯率市場間的波動溢出效應；Worthington和Higgs(2004)運用BEKKGARCH模型檢驗了亞洲市場間的波動溢出關系；都取得了良好的估計效果，國內文獻中主要在對中國股票市場研究中介紹或使用過該模型，期、現貨市場間波動性研究尚沒有文獻涉及。

本文目的是考察上海金屬期貨與現貨市場間的波動性關系，建立二維的非對稱BEKK-GARCH模型，參數方陣Aik、Bik和Git中，令i=1,2，其中1代表現貨市場，2代表期貨市場。二維非對稱BEKK-GARCH模型的展開式可以表示為下面（6）式的形式，其中對角線參數反映各市場自身的相關關系；非對角線參數（a12,a21）、（b12,b21）反映期貨與現貨兩市場間的波動溢出效應；（g12,g21）反映期貨與現貨兩市場間的波動非對稱性。本文考察重點是上海金屬期、現貨兩個市場間的溢出效應，我們將針對模型參數方陣中非對角線元素的非線性組合進行似然比LR統計量和Wald統計量的檢驗。對上海鋁、銅期、現貨市場之間的波動溢出效應作如下檢驗：

（1）原假設 H0:a12=b12=0,a21=b21=0，不存在期貨與現貨市場間雙向的波動溢出效應；

（2）原假設H0:a12=b12=0，不存在現貨市場對期貨市場的單向波動溢出效應；

（3）原假設H0:a21=b21=0，不存在期貨市場對現貨市場的單向波動溢出效應；

（4）原假設H0:g12=g21=0，不存在期貨與現貨市場間雙向的波動非對稱效應；

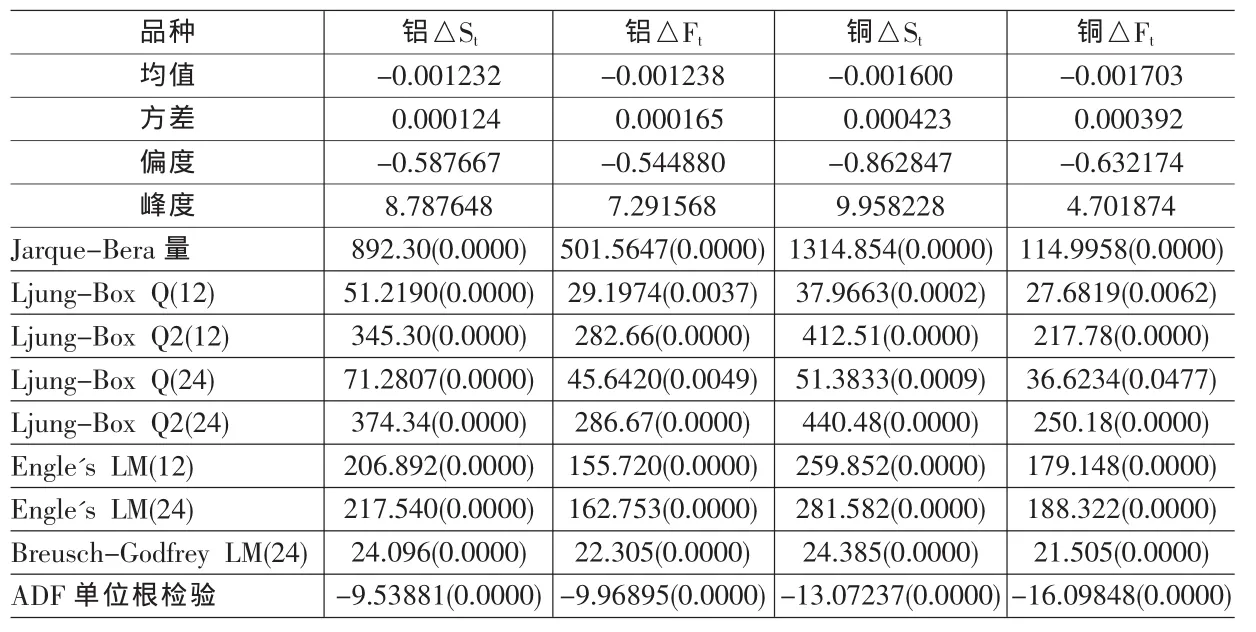
表1 描述統計、ARCH效應檢驗結果

2 數據說明與ARCH效應檢驗

2.1 數據說明

本文研究數據選取上海期貨交易所鋁連續、銅連續合約日收盤價，以及對應期間上海有色金屬市場鋁、銅現貨的日價格。鋁期貨與現貨數據樣本期為2006年5月18日至2008年12月9日，共計近30個月615個交易日；銅期貨與現貨數據樣本期為2006年5月30日至2008年12月9日，共計近30個月615個交易日；數據來源于長江有色金屬市場網站歷史數據資料和彭博期貨行情軟件。交易日的現貨價格與期貨收盤價，那么現貨日收益率與期貨日收益率則分別St為Ft與的一階差分，表示為△St與現貨市場的價格序列定義為St=Ln(Pt)，期貨市場的價格序列定義為其中分別是第 t個△Ft，即△St=Ln(Pt/Pt-1)，

2.2 描述性統計和ARCH效應檢驗

分別對鋁、銅現貨、期貨市場日收益率序列進行描述性統計分析，和收益率序列自相關的Ljung-BoxQ統計量檢驗、Engle拉格朗日乘數（LM）檢驗、Breusch-Godfrey LM高階序列相關檢驗方法，來檢驗收益率殘差的方差是否存在條件異方差，并且對序列進行平穩性的ADF檢驗，結果見表1：

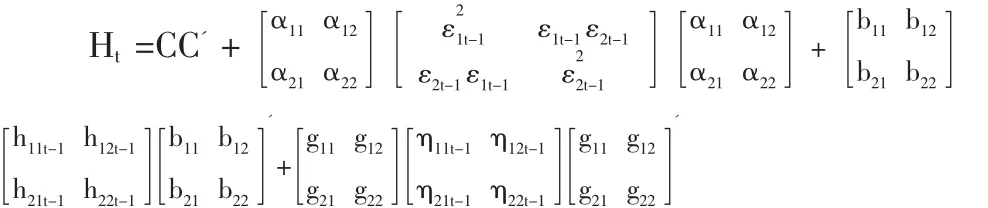
從表1結果可知，在樣本期，鋁期貨市場的方差大于現貨市場，表明鋁期貨市場價格波動程度大于現貨市場，而銅市場正好相反，銅現貨市場價格波動程度大于期貨市場；鋁、銅現貨、期貨市場從偏度來看，均為左偏的，銅市場的偏度較大；從峰度來看,鋁、銅現貨、期貨市場的峰度均大于3，Jarque-Bera統計量均奇大，說明鋁、銅現貨、期貨市場均呈現“尖峰厚尾”的分布，并不能完全符合正態分布。Ljung-Box Q、Engle LM、Breusch-Godfrey LM檢驗統計量的概率值均顯著為0，說明鋁、銅現貨、期貨市場收益率的殘差序列均存在條件異方差，即收益率的波動具有隨時間推移而改變的自回歸條件異方差（ARCH）現象，而且ADF單位根檢驗鋁、銅市場日收益率序列均為平穩序列，適宜于建立ARCH族模型進行分析。

3 實證結果

上海鋁、銅現貨、期ARCH效應，建立非對稱向量BEKK-GARCH(1,1)模型進行實證分析，檢驗現貨收益率與期貨收益率間的波動溢出效應是否存在，以及波動溢出是否呈現非對稱性。本文采用無約束最貨市場收益率均具優化BFGS（Broyden，Fletcher，Goldfarb 和 Shanno）算法來估計使模型似然值極大的參數向量，分別正態分布、t分布和廣義誤差分布（GED）的假設下，并依據AIC值最小準則選擇最優模型。表2為式(6)的估計結果，包括收 益率波動的持續性、自身波動的非對稱性、波動溢出效應、波動的非對稱性等信息，表3為兩市場之間波動溢出及波動的非對稱效應檢驗結果。由表2和表3可得：

（1）從鋁、銅現貨、期貨市場收益率序列自身波動看，即式（6）中Aik、Bik的對角線元素，僅鋁期貨前一期誤差項不顯著，其余各參數均在1%置信水平下顯著，說明各序列自身波動有明顯的持續性；現貨、期貨市場間，在式（6）Aik中的非對角線元素，只有鋁現貨與期貨市場間具有波動的持續性。

（2）從收益率序列自身波動的非對稱性看，即式（6）中的gik對角線元素，除鋁現貨外，其余均顯著性，說明鋁現貨不存在“熱波”效應，即鋁現貨市場對前一期的“消息”的沖擊沒有明顯反應；鋁期貨、銅現貨和銅期貨估計系數均顯著不為0，說明從自身收益率序列看，存在波動非對稱的杠桿效應，即對各自市場前一期的“消息”沖擊有明顯反應；

（3）從現貨與期貨收益率間的波動溢出效應來看，即式（6）中Bik的非對角線元素，鋁現貨與期貨估計系數在1% 顯著水平下均顯著，說明鋁現貨與期貨市場間具有顯著雙向跨市場波動溢出效應，既具有“流星雨”效應；而銅市場估計系數均不顯著，說明銅現貨與期貨收益率變動波動性沒有顯著的跨市場波動溢出效應。

（4）從現貨與期貨市場間波動非對稱性方面看，即式（6）中gik的非對角線元素，在鋁市場估計系數均顯著不為0，鋁現貨、期貨市場間均具有波動的非對稱性，說明在鋁現貨、期貨市場都對來自對方市場的“消息”有明顯反應；在銅市場估計系數也均顯著不為0，說明銅現貨、期貨市場間雖沒有顯著的波動溢出效應，但市場間卻存在著顯著的波動非對稱效應，這一點與Koutmos和Tucker(1996)等人的研究結論相似。

4 結論和未來研究的建議

本文樣本期處于“大熊市”時期，期間又爆發了美國“次貸”危機引發的金融“大海嘯”，對國際金屬市場產生重大影響，在此背景下并結合國外學者及華仁海、劉慶富、張金清等國內學者的相關文獻分析如下：

（1）本文結論上海銅市場間的波動溢出效應不顯著，與張金清(2006)、劉慶富(2007)的研究結論不相符，本文樣本期間位于兩人研究期間之后，說明上海銅期貨與現貨存在顯著的雙向波動溢出效應,而銅市場間則不顯著,我們認為這并不能作為比較兩市場成熟程度的依據,兩市場這樣的差異,可能與兩種金屬在中國的儲藏量、生產量的差異有關，這種差異的存在，造成兩市場所受到的影響信息來源上存在不同。結合華仁海（2005），張金清（2006）、劉慶富（2008）的研究結論，可能與銅期貨市場的國際化市場間，收益率的波動溢出效應并不是始終存在，不具有一貫性，可能會隨市場情況的變化而發生變化，正如Gwilym and Buckle(2001)所指出市場景氣循環也是收益率波動效應的重要決定因素；也可能如Min和Najand.(1999)D對韓國KOSPI(200)指數期、現貨市場的研究發現市場間波動溢出效應存在顯著的樣本依賴。

表2 非對稱波動溢出效應估計結果

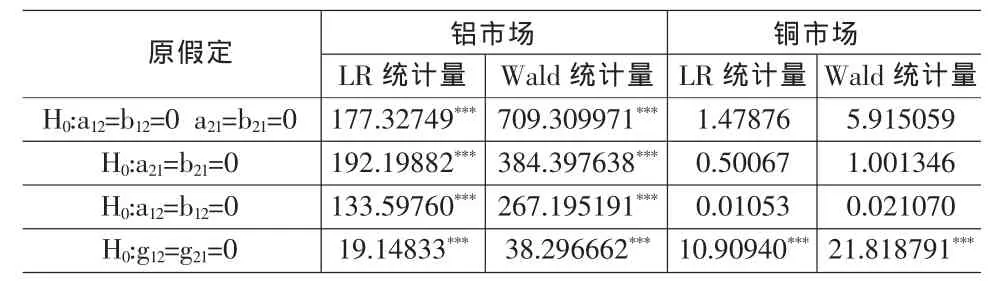
表3 期、現貨兩市場之間波動溢出及波動的非對稱效應檢驗

（2）在樣本期的“大空頭”市場，上海鋁、銅期貨、現貨市場間波動溢出效應表現不同，鋁期貨與現貨市場間程度相對較高有關。

（3）上海金屬期貨與現貨市場間存在顯著的波動非對稱性的杠桿效應，這一點與張金清(2006)、劉慶富(2007)的結論相符，在“大熊市”和國際金融危機的雙重打擊下，期、現貨兩市投資者都對來自對方市場的信息有著敏感的反應，但實證結果并不能解釋銅市場間的波動非對稱效應的產生機理，可能與上海銅期貨、現貨市場分別受到國際銅期貨、現貨市場的較強影響有關。

（4）本文以及國內相關文獻實證研究中，還存在著沒有考慮收益率序列均值樣本期在不同域之間變化的問題，忽略域變特點可能會造成波動性測量值相對于真實值出現偏差，從而影響實證結論的精確程度。因此有關中國期、現貨市場間波動性的研究還有待進一步的深入。

[1]Black,F.Studies of Stock Markets Volatility Changes,Proceedings of the American Statistical Association[C].Business and Economic Statistics Section,1976.

[2]Stephen A.Ross.Information and Volatility:The No-Arbitrage-Martingale Approach to Timing and Resolution Irrelevancy[J].The Journal of Finance，1989,44(1).

[3]Robert F.Engle,Takatoshi Ito,Wen-Ling Lin.Meteor Showers or Heat Waves?Heteroskedastic Intra-Daily Volatility in the Foreign Exchange Market[J].Econometrica,1990,58(3).

[4]Chui-Chun Tsai,Tsun-Siou Lee.An Investigate on Information Transmission ofNearby-Month Taiwan Stock Index Futures during Trading,Nontrading,and between Trading and Nontrading Period:Price Discovery and Content of Price Volatility[J].Journal of Financial Studies,2004,12(1).

[5]Koutmos,G.,Tucker M.Temporal Relationships and Dynamics Interactions between Spot and Futures Stock Markets[J].Journal of Futures Markets,1996,16(1).

[6][臺灣]蔡垂君,李存修.臺灣股價指數與指數期貨跨市場價量訊息傳遞關系之實證研究-價格發現與價量關系[J].中華管理評論(國際學報),2004,7(2).

[7]Angelos.Kanas.Volatility Spilloversbetween Stock Returnsand Exchange Rate Changes:International Evidence[J]..Journal of Business Finance&Accounting,Blackwell Publishing,2000,27.

[8]華仁海,劉慶富.國內外期貨市場之間的波動溢出效應研究[J].世界經濟,2005,(8).

[9]張金清,劉慶富.中國金屬期貨市場與現貨市場之間的波動性關系研究[J].金融研究，2006,(7).

[10]劉慶富,仲偉俊.我國金屬期貨與現貨市場之間的價格發現與波動溢出效應研究[J].東南大學學報(哲學社會科學版),2007,(5).

[11]R F Engle,KF Kroner.Multivariate Simultaneous Generalized ARCH[J].Econometric Theory,1995,11.

[12]張世英,樊智.協整理論與波動模型——金融時間序列分析及應用[M].北京:清華大學出版社,2004.

(責任編輯/易永生）

F724.5

A

1002－6487（2010）17－0150-03