基于馬爾可夫轉換模型的中國股市波動性研究

葛文雷，居新華

（東華大學 旭日工商管理學院，上海 200051）

基于馬爾可夫轉換模型的中國股市波動性研究

葛文雷，居新華

（東華大學 旭日工商管理學院，上海 200051）

證券價格的波動變化不僅影響衍生產品的價格也是政府管理金融市場、制定政策的依據。由于價格的波動往往呈現非線性的特征，文章利用馬爾可夫轉換模型對中國股票波動性進行估計。研究發現該模型可較好對我國上海證券市場股價波動性進行分類估計，并得到了證券市場波動的狀態平滑概率圖。在統計結果的基礎上，還分析了我國市場波動性的成因和特點，并對政策的有效性進行評述。

馬爾可夫轉換模型；股票波動性；羊群效應

0 引言

證券市場作為金融體系的一個組成部分，在金融體系中具有重要的地位，證券市場波動對整個金融體系具有極其重要的影響。按照現代資本市場理論的觀點，證券市場中各類因素的變化，都會不同程度地影響證券市場的供求關系并最終反映在證券市場價格變動上。因此價格波動就成為證券市場波動研究最核心的內容。

影響股票價格變動的因素可分為三類：（1）政策性因素，即管理層的政策干預行為，如股票交易規則變更、印花稅的調整、通過新聞媒體發表的重要言論等。（2）外部性因素，主要指熱錢，匯率等能影響股市流動性的因素。（3）周期性因素，每年初公司都會集中公布上年度年報，這段時間證券市場所接受的信息要比其他期間的要多，也會對股價的波動性產生影響。

國內學者對影響股價波動的因素進行過一些實證研究。但是這些研究往往針對證券市場某一特定時期進行統計，缺少對影響證券市場波動各種因素的整體分析：比如證券市場處于什么狀態時，市場波動性會較小；這種關系是否具有時間一致性；市場波動性大的時候，是由單個因素影響還是幾個因素共同影響。為解決上述問題，本文利用非線性下的馬爾可夫轉換模型對上證綜指收益的波動率進行系統研究。把證券市場按股票收益率波動性的大小分成兩類，通過狀態轉移矩陣研究不同時期的波動性大小，將不同時期波動性與該時期影響股市的因素聯合分析，考察我國證券市場收益率變動的特點。

1 建立模型

馬爾可夫轉換模型是一種研究時間序列結構性變化的方法，它通過外部數據計算系統內部處于何種不可觀測的體制的概率，來對系統進行分析和預測。馬爾可夫轉換模型由Hamilton（1989）首先建立,用于研究美國經濟周期，Hamilton發現美國GNP增長率趨勢函數可用一階馬爾可夫過程在兩種不同的狀態之間切換來表示，這兩種狀態反映了經濟周期的狀態：正向的經濟增長狀態和負向的經濟衰退狀態。所以馬爾可夫轉換模型適合研究不同狀態下股市的波動率。

傳統AR(p)模型下的股票波動率yt模型為：

其中 Xt=(yt-1,yt-2，…，yt-p)，φ 為 Xt的回歸系數，ut為白噪音。

在馬爾可夫轉換模型下，假設股票波動率y(t)存在k個服從AP(p)時變回歸方程，它們分別代表k個不同狀態，其中狀態St為一不可見隨機變量，且St是關于時間t齊次的，具有狀態空間J=(1，2，…，k)一階馬爾可夫過程，其轉移矩陣為：

其中

對任意 i∈J，都有

則基于馬爾科夫轉換下股票波動率可表示為：

其中 Xt=(yt-1,yt-2， …，yt-p)，φSt為 Xt在狀態 St下的回歸系數，殘差服從 ut(0，)分布，隱含狀態 St滿足式（3）和式（4）。

若隱含狀態S=(Sp+1，…，Sn)是已知的，那么模型中不同狀態下的未知參數Θ（包括AR(p)中截距、回歸系數以及殘差）可以通過對數極大似然估計方程得到：

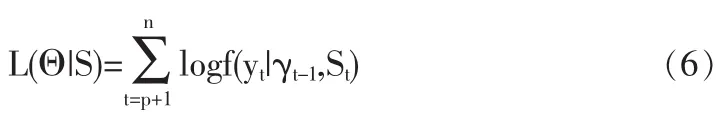
這里γt-1代表在t-1時刻證券市場所有已知的信息，對Xj(j≤t)中所有的觀察值均滿足：

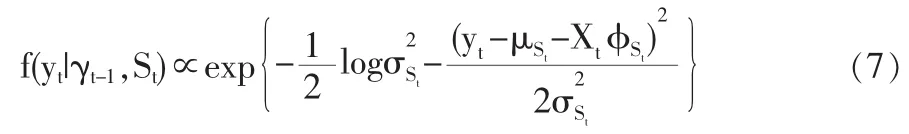
但是，狀態S是通常是觀察不到的，所以必須利用已知數據進行估計。當狀態S是隱含的時候，AR(p)馬爾可夫轉換模型的需估計的未知參數Θ，除式（6）中的之外，還包括對轉移概率矩陣P的估計。通常用下面辦法解決該問題。

利用全概率公式，可將對數似然估計方差寫成如下形式：

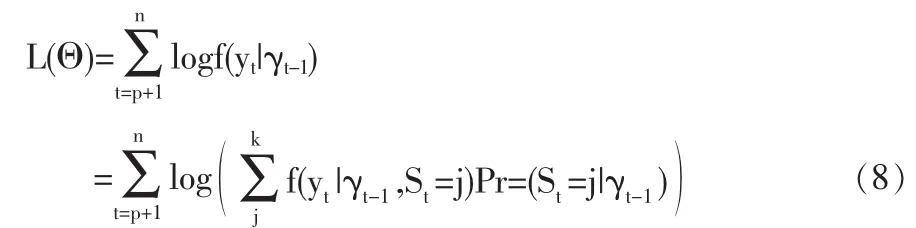
這里 f(yt|γt-1,St=j)符合式（6）。 并根據貝葉斯定理，Pr(St=j|γt-1)可以寫成

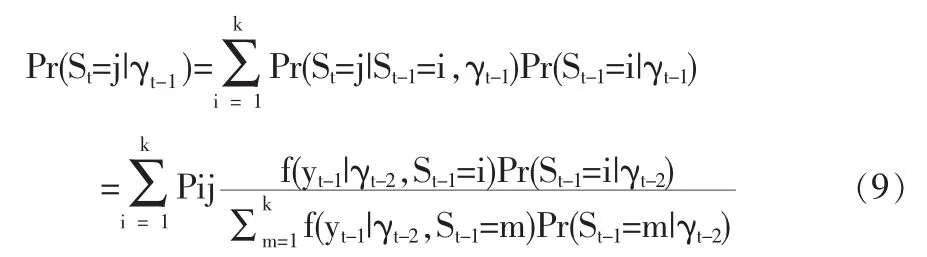
因此，對每個狀態的初始概率進行估計后，AR(p)馬爾可夫轉換模型的對數似然估計方程可以利用式（8）和式（9）得到，同時利用極大似然估計法就可以確定每個參數的估計值。

馬爾科夫狀態轉換模型中的狀態變量雖然不可直接觀察到，但可以通過上述方法推論任意時刻t狀態的概率,基于t時刻得到的概率為過濾概率，基于全部觀測值得到的概率為平滑概率，由于馬爾可夫轉換模型中的狀態概率為內生決定，由數據自行分割、識別各狀態期間，因而避免了研究者主觀設定和選擇問題。

2 參數估計

樣本數據取自1993年1月1日至2008年7月1日上證綜指每周收益率的波動率。數據來源色諾芬數據庫（CCER）。上證綜指每周收益率的時間序列如圖1。

每周收益率的波動率RVOL通過下面方法得到：先將該周每日收益率的平方，將5天的數據求和，最后將得到的和開方，該波動率可以反映該周股票波動率的大小，如圖2所示。

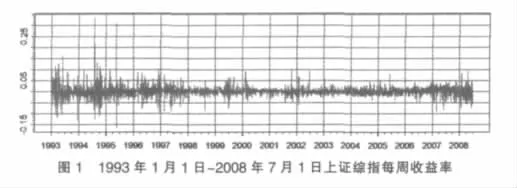
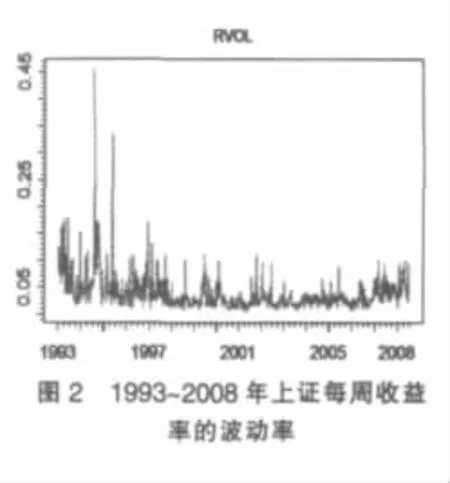
表1 樣本數據的非線性檢驗

由于樣本的時間跨度很長，所以首先對該時間序列進行非線性檢驗，結果如表1。

檢驗結果p-value小于0.05，所以統計意義顯著，原假設不成立，即該序列存在非線性狀態轉移，因此不適合用單個時間序列對收益率的波動率進行估計。

本文利用AR(2)馬爾可夫轉換模型對數據進行研究。假設證券市場狀態分為兩種：穩定狀態，和不穩定狀態。穩定狀態下，證券市場受信息沖擊較小，其股指波動率也較小；不穩定狀態下，證券市場受信息沖擊較大，股指波動率也大。狀態隨機變量僅僅取1，2值，狀態之間表現為非連續的轉換。此時股指變動率的馬爾可夫轉換模型為：

當S=1時：

當S=2時：

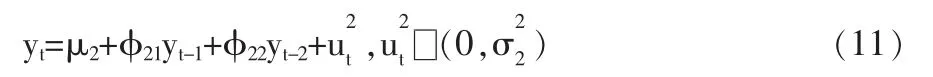
狀態轉移概率為：

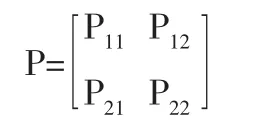
下面利用上一節提到的方法對參數 Θ=（μ1，μ2，φ11，φ12，φ22，σ1，σ2，P11，P12，P21，P22）進行估計。 在進行估計之前，為使數據更加正態化，將數據進行對數處理。利用處理后的數據，對馬爾可夫轉換模型進行參數估計的結果如表2所示。

從表2可知大多數參數的估計值都有重要的統計意義。由于這是基于對數的參數，所以還需將結果還原成要進行估計的參數Θ，還原后的馬爾可夫轉換模型為：

當S=1，股市狀態穩定時：

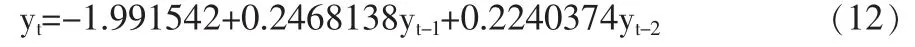
當S=2，股市狀態不穩定時：

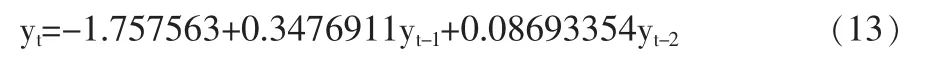
狀態轉移概率為：

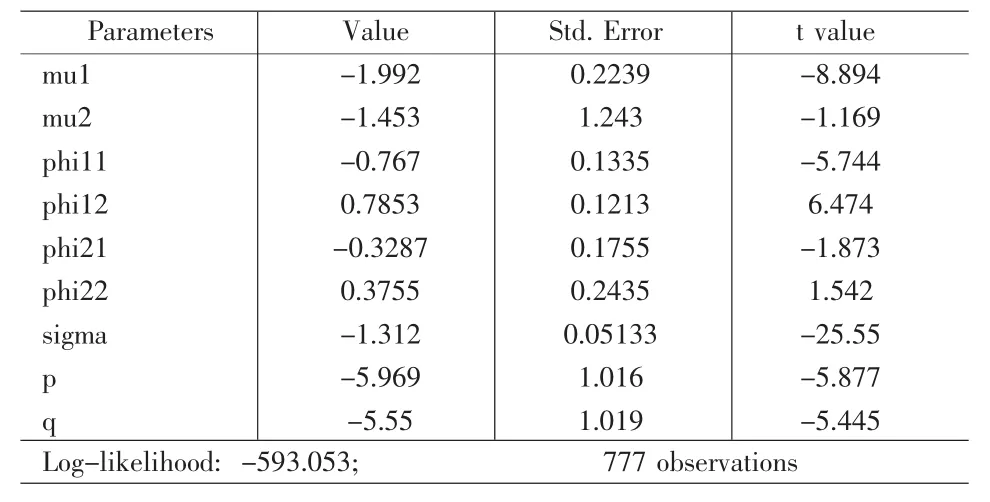
表2 馬爾可夫轉換模型參數估計

式（12）說明股市在穩定的狀態，前兩周的波動率與該周的波動率有很好的線性關系，而且兩者權重差別不大。式（13）說明股市在不穩定狀態下，該周的波動率與前一周的波動率相關，而與前兩周的波動率關系很小，這是由于股市在不穩定狀態下，新信息對市場沖擊要比穩定狀態下對市場的沖擊大。

式（14）說明股市從穩定狀態到穩定狀態的概率為99.7%，而從不穩定狀態到不穩定狀態的概率為99.6%，若該時間序列是平穩的，通過式（14）可得兩種狀態下無條件概率：

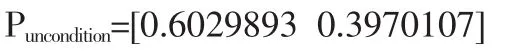
說明狀態穩定的無條件概率為0.6，狀態不穩定的無條件概率為0.4，證券市場大部分時間還是處于穩定狀態下。

3 模型解釋

本文目的是對中國證券市場波動性整體變化進行分析，即考察某一時點下市場狀態的概率值，也就是對Pr(St=j|γt)進行估計。利用式（9）和實證檢驗所得的對參數的估計值，可得到全樣本估計時狀態1（穩定狀態）的平滑概率圖，表示穩定狀態在各個時點的概率大小，如圖3。

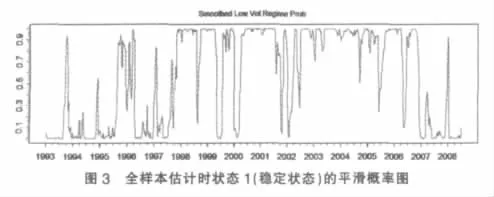
從圖3中，可將上海證券市場從1993～2008年分成三個時期。第一個時期從1993～1998年。這個時期是證券市場初創時期市場波動性大。該時期投資者還沒有形成成熟的理性投資理念，政策在該時期的影響尤為顯著：1994年7月底的“三大政策”救市，1995年停止國債期貨交易以及1996年下半年至1997年上半年的一系列政策調控等。雖然這一系列政策目的是在于建立相對穩定的政策調控機制，但由于采取措施的強烈行政性和強制性特點，在中國市場規模相對還不是很大的情況下，結果往往造成了價格暴跌與暴漲，加之該時期沒有漲跌停板和T+1交易的限制，更加劇了市場波動性。

第二個時期從1998～2006年中期，這段時期股市比較穩定。1998年6月降低印花稅和央行降息兩大消息促進了股市的波動，但很快與9月份波動就歸于平穩。同樣1999年6月央行全面降息也讓股市瘋狂了3個月。2000年初央行允許券商、基金投資公司進入銀行間債券市場以及證監會改革股票發行方式也讓股市從穩定狀態轉變為不穩定狀態。之后股市進入緩慢上漲狀態，而且波動比較穩定。2001年6月的國有股減持政策的推出，股市反映強烈，之后中石化破發，《證券公司管理辦法》、《上市公司治理準則》等出臺使的這次波動持續一年之久才歸于平靜。而且股市對政策的影響的承受應能力也在加強。2005年4月啟動的股權分置改革，是這段時期最后一次波動并持續了三個月。

第三個時期從2006年中期至2008年7月。影響這段時間股價波動的因素很多，主要有匯率制度的變動，導致熱錢的大量涌入；房地產行業調控，使得資金流入股市；當然最主要還是全民炒股。投資者的“羊群效應”導致了證券市場波動率的放大，引發證券市場大的震蕩。雖然在這當中政府曾通過調整印花稅，來減少波動性。但在此氛圍下，這些政策事件對證券市場影響的信號也理所當然被放大，引起證券市場產生大的波動。而“牛市”中的“利好”政策和“熊市”中的“利空”政策就更容易產生“羊群效應”，因為這種政策信息更符合大多數人的判斷。

4 結論

本文利用馬爾可夫轉換模型對中國股票波動性進行研究。利用上證指數歷史數據對模型的參數進行估計，并得到了證券市場波動的狀態平滑概率圖。研究發現該模型可較好對我國上海證券市場股價波動性進行估計。利用統計結果分析了我國證券市場波動性的成因和特點。該模型不僅可以用來為政策的制定提供依據，而且對金融衍生品的定價也有一定參考意義。

[1]Hamilton J.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle[J].Econometrica,1989,（57）.

[2]Kim C J.Dynamic Linear Models with Markov Switching[J].Journal of Econometrics,1994,（60）.

[3]Hamilton J.AnalysisofTimeSeriesSubjecttoChangesin Regime[J].Journal of Econometrics,1990,（45）.

[4]許均華，李啟亞等.宏觀政策對我國股市影響的實證研究[J].經濟研究，2001，（9）.

[5]彭文平，肖繼輝.股市政策與股市波動[J].上海經濟研究，2002，（3）.

[6]鄒昊平，唐利民，袁國良.政策性因素對中國股市的影響:政府與股市投資者的博弈分析[J].世界經濟，2000，（11）.

[7]趙振全，張宇.中國股票市場波動和宏觀經濟波動關系的實證分析[J].數量經濟技術經濟研究，2000，（6）.

[8]嚴武，肖民贊.我國股市收益波動特征及政策因素影響分析[J].當代財經，2005，（12）.

[9]唐齊鳴，李春濤.影響上海股市波動的因素分析[J].數量經濟技術經濟研究，2000，（11）.

（責任編輯/浩 天）

F830.91

A

1002-6487（2010）17-0153-03

葛文雷（1947-），男，上海人，教授，研究方向：金融證券、公司財務。

居新華（1970-），男，江蘇人，博士研究生，研究方向：公司財務。