基于自記憶原理的深基坑位移預測方法

王 偉,謝學斌,黃 東

(中南大學 資源與安全工程學院,湖南 長沙410083)

對基坑變形進行準確的監測和有效的預測是基坑工程成敗的關鍵因素之一[1]。目前采用較多的預測方法是利用深基坑位移監測時間序列,建立各類時序分析模型的方法。深基坑位移預測的時間序列方法主要有:灰色理論預測方法[2-3];時間序列分析方法[4],如AR模型,ARMA模型;智能算法[5-8],如BP神經網絡算法,RBF神經網絡算法,遺傳算法;組合預測方法[9]。以上每種方法各有其適應條件及優缺點,如灰色理論模型適用于累加生成數列具有灰指數規律,但有一些時間序列的累加生成數列常常不具有灰指數規律,因此預測出的數據就會存在較大誤差。

自憶性原理強調系統的前后承續性,強調系統自身演變對過去歷史的依賴。也就是要預測未來,就得立足現在,回溯過去。對于只有一組時間序列值的系統,如深基坑支護系統一般只有一系列動態觀測值,此時,可把現有觀測資料看作描述實際非線性系統動力模式的一系列特解,通過反演計算得到描寫系統的非線性動力模式。求得系統的動力模式后,建立自記憶模型進行系統模擬或預報[10]。這種方法不需要分析確定影響深基坑支護系統位移變化的主要因素,也不需要收集整理與深基坑支護系統位移動態觀測序列相應的多種影響因素數據,避免了大量數據的收集整理,只涉及深基坑支護系統位移觀測序列本身,方便實用且具有較好的預測精度。

1 系統自記憶原理與建模[11-12]

1.1 自憶性原理

設系統演化動態方程組可寫為

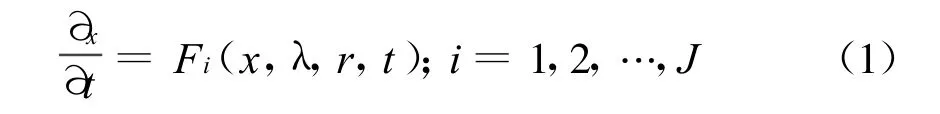
式中J—整數;x—為第i個變量;λ—參數;r—空間;t—時間。

為簡便計,下文只考慮單個變量x。設所討論的變量和函數皆連續、可微、可積,定義記憶函數β(r,t)∈ H,β為r,t的函數 ,且|β(r,t)|≤1,在以下推導中固定在空間點ri上,故在β中省去r,在上式中省去i,在希爾伯特空間中定義內積

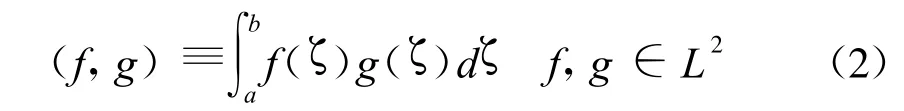
將式(2)定義的內積運算運用到式(1)上得

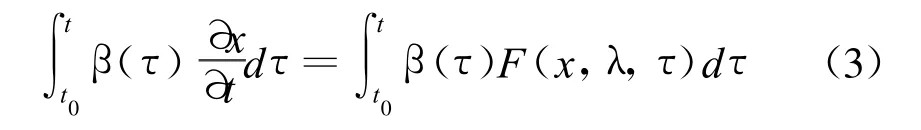
顯然式(3)為對式(1)的一種加權積分,權重即為記憶函數。

運用分部積分及微分中值定理對式(3)進行變換和運算,并令,其余符合類推,可以得到

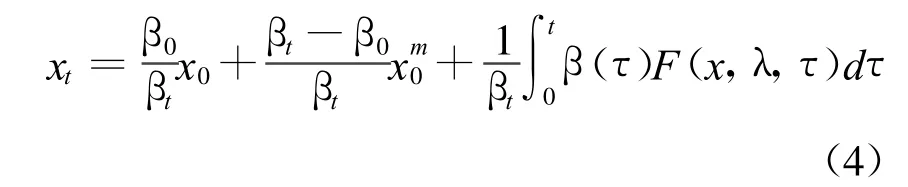
對于多個時次 ti,i=-p,-p+1,…,0,1,對式(1)進行積分并進行以上類似處理可得

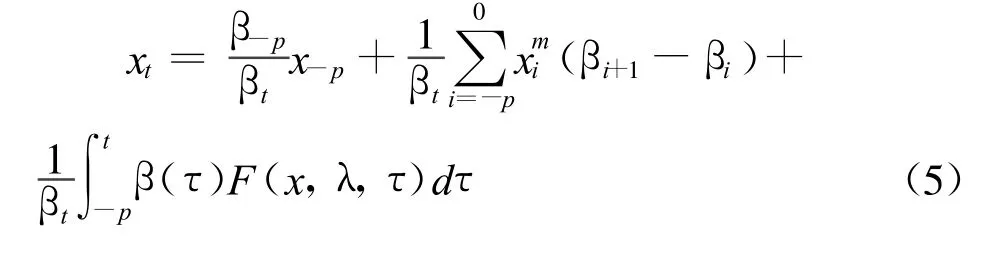
這是一個差分-積分方程,稱它為自憶性方程。令 p=0,則式(5)變為式(4),稱式(4)為 0階自憶性方程,式(5)為p階自憶性方程。

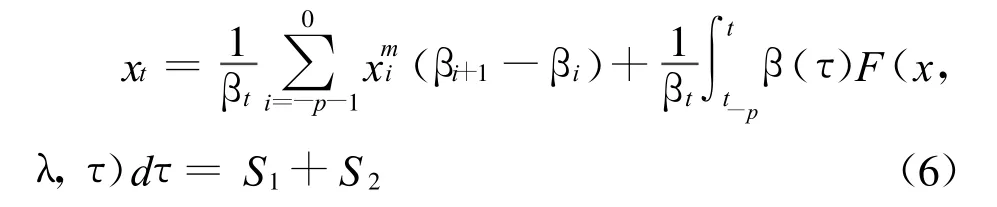
由式(6)可知,在ri點的預報值在時次t的值由兩項組成。只涉及到本空間點(即 ri點)的初始時次t-p和中間時刻的值,故稱S1為自憶項;而S2為其他空間點對ri點在時間間隔[t-p,t] 中的總效應,故稱為他效項。式(6)的物理意義是,第ri點在時次t的x值等于本點過去x值的自憶效應加上源函數F(x,λ,t)與記憶函數乘積的累計和。

1.2 自記憶方程的離散表達

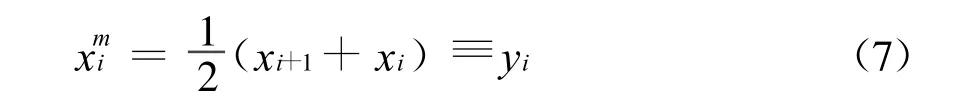
設時次為t,t0,t-1,…,t-p,取等距時次間隔,可令△ti=ti+1-ti=1。將 βt和βi合寫,則得離散形式的自憶性方程

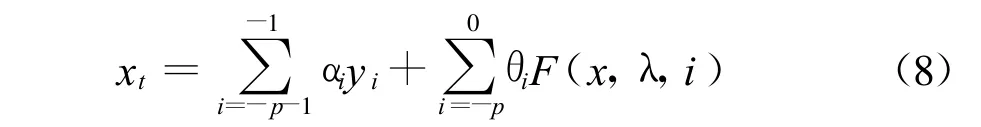
1.3 記憶系數的求解

正如只有很少量微分方程有解析解,自憶性方程也一樣。因此只有用計算機求其數值解。用L個時次的歷史資料,用最小二乘來求記憶系數 αi,θi,設空間共 N 個點 。記

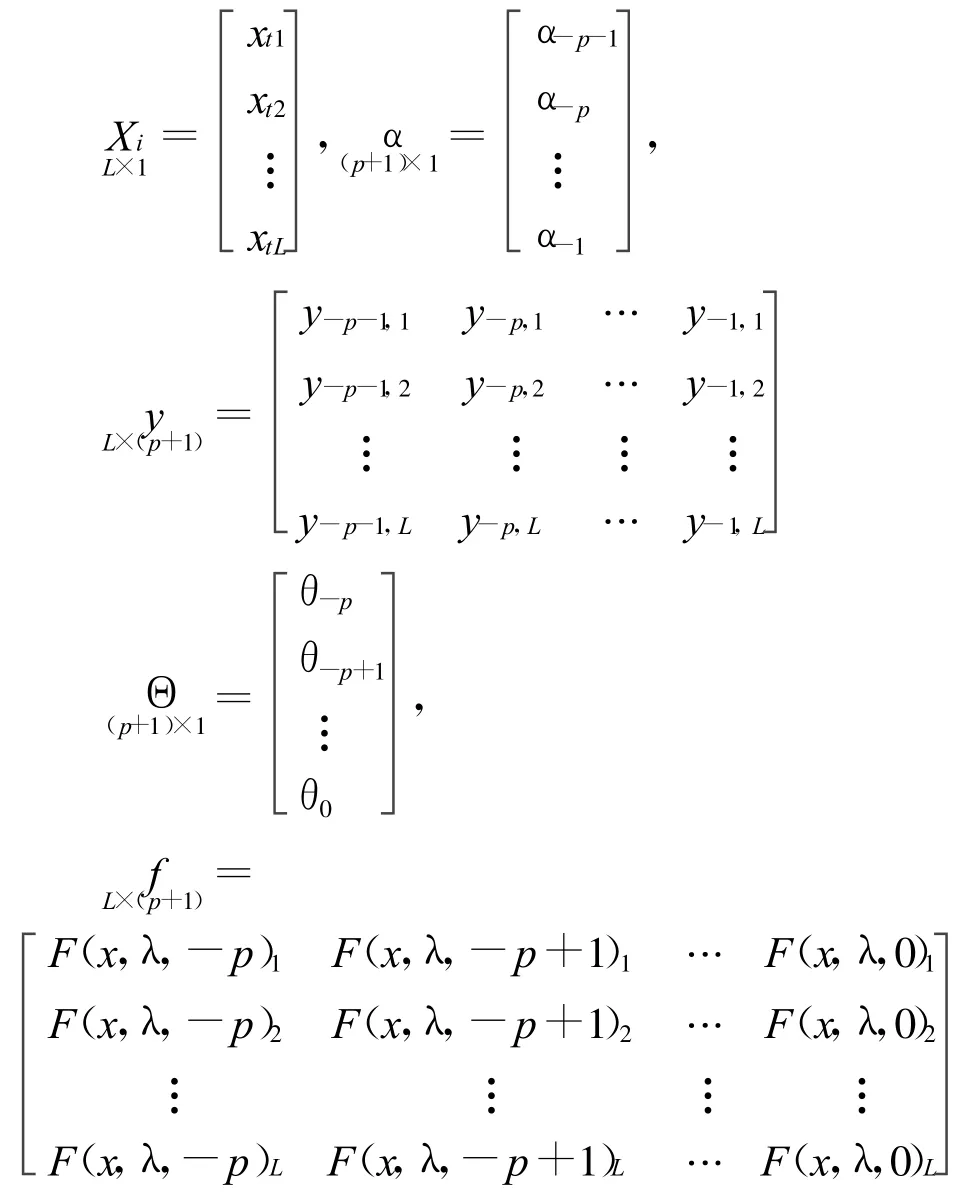
可得矩陣方程為

令

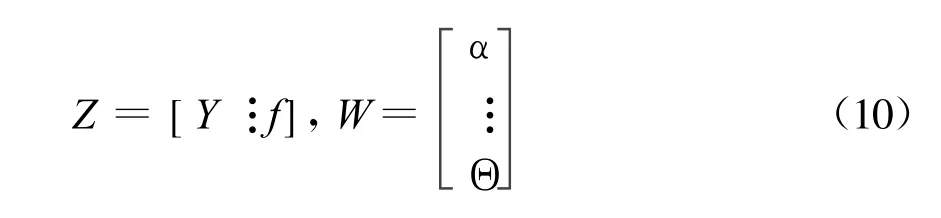
則式(9)變為

其最小二乘解為

求出系數矩陣W后就可以對時間序列進行擬合和預測,最后還原為原始數據。

2 趨勢曲線模型[13-15]

趨勢曲線預測模型即假設數據變量大致沿某一趨勢曲線變化,從而用曲線方程模擬這一變化,進而對未來數據進行預測。常用的為多項式趨勢曲線。

假設多項式趨勢曲線為

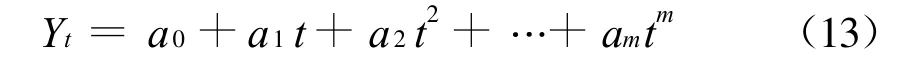
當函數的個數等于m+1時,能唯一解得所有的待定參數,當函數值的個數大于m+1時,按最小二乘法也能唯一解得所有的待定參數。待求得所有待定參數后可得到趨勢曲線預測模型為^Yt=

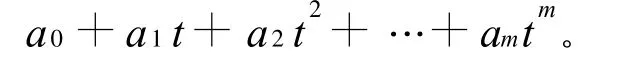
3 趨勢曲線-自記憶模型的建立

基于物理運動不可逆性提出的自記憶性原理,針對有微分方程描述的動力系統,可以建立相應的自記憶模型。但在很多情況下往往只有時間序列觀測值,而沒有現成的描寫系統的微分方程。如果對一次累加(1-AGO)時間序列x(1)(i)求多項式趨勢曲線為f(x)=a0+a1t++…+,一次累加生成序列x(1)(i)可視為函數f(x)在ti處的離散點,即X(1)(i)=a0+a1ti+對上式求微分既可得到系統動力微分方程以此式作為系統動力微分方程可以建立趨勢曲線-自記憶組合預測模型。

4 工程實例

取某工程2009年6月13日到2009年9月26日監測數據,每隔三天取一個監測數據,見表1。

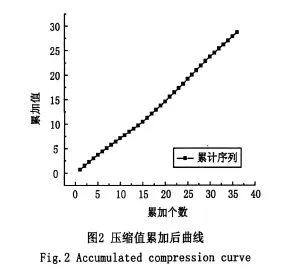
首先對表1中數據系列按除以最大值的方法進行壓縮處理,使各數值均變換到0至1之間(圖1),再對其進行一次累加生成(1-AGO),得X(1)(圖2)。從圖1和圖2可以看出,原始序列X(0)為一波動較大的不規則時間序列,難以用解析函數擬合,而經過一次累加生成序列X(1)具有較明顯曲線特性,可以對其進行趨勢曲線擬合。

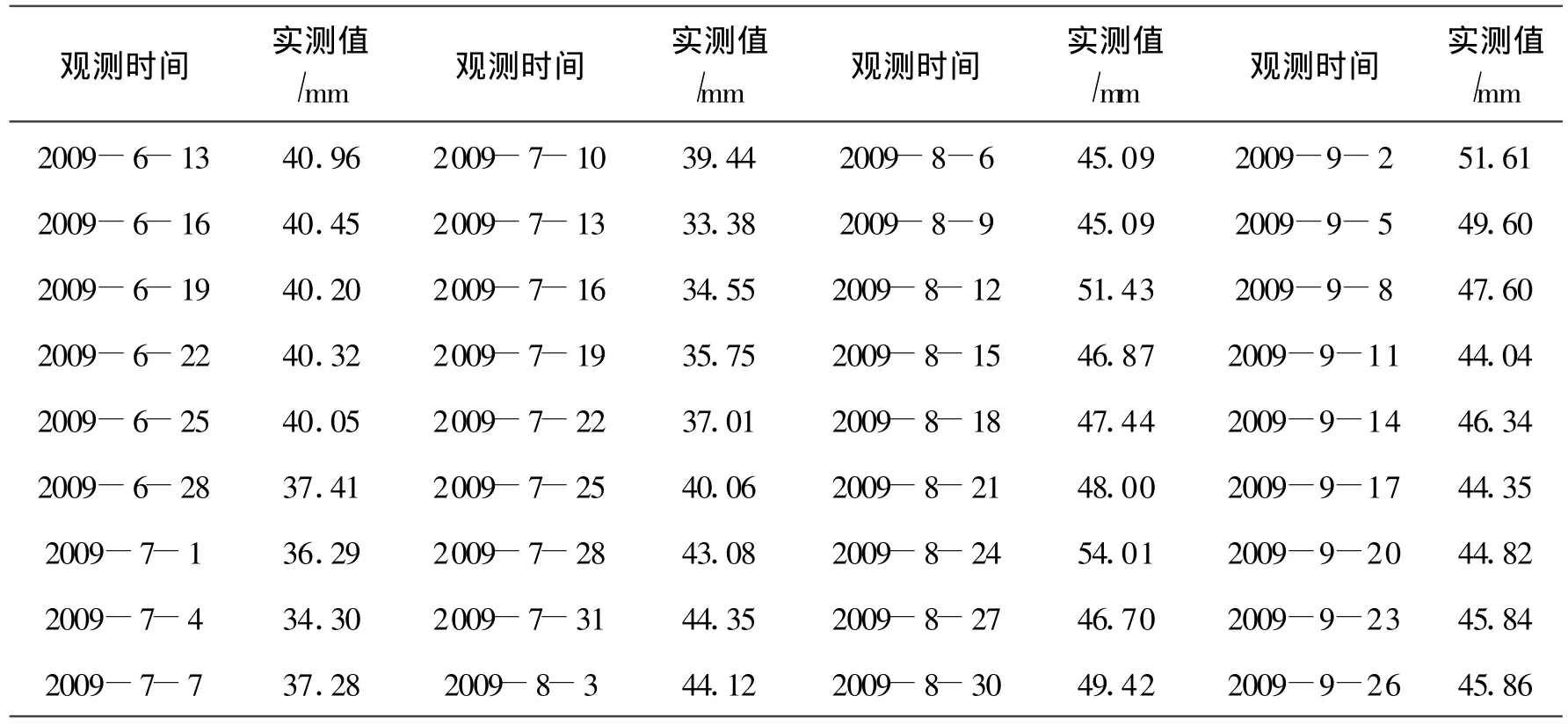
表1 監測點監測數據Tab.1 Monitoring data of one monitoring point

分別用上述建立的兩種預測模型和灰色GM(1,1)模型對表1中2009年6月13日到2009年9月8日的位移監測數據進行擬合計算,并對2009年9月11日到2009年9月26日的監測數據進行預測檢驗。

4.1 灰色GM(1,1)模型

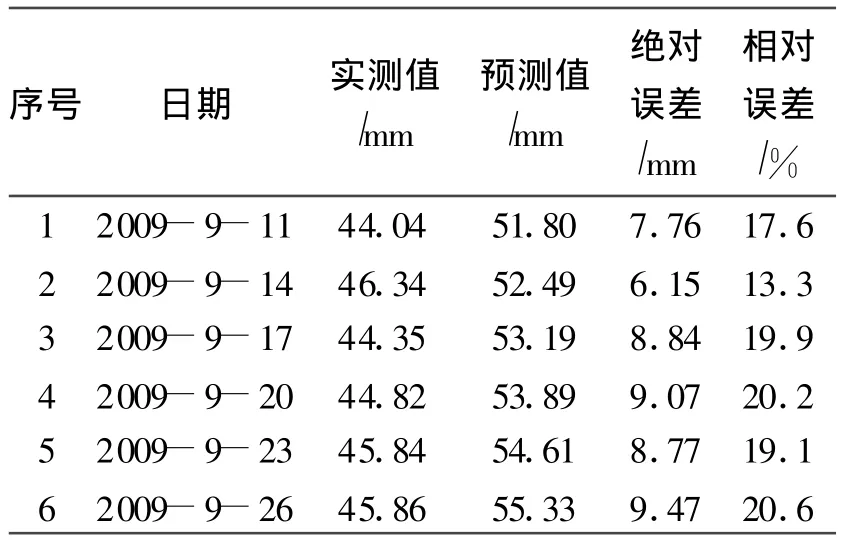
表2 灰色GM(1,1)模型預測值與監測值比較Tab.2 Comparison between monitoring values and predicted values

對X(1)擬合成一階線性微分方程,并按最小二乘法求解,得最小二乘估計參數數列^a=(a,b)T=(-0.01317,0.64037)T。則時間響應函數為

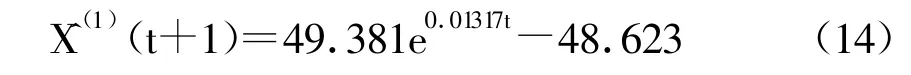
再做累減生成,可得模型的還原擬合值

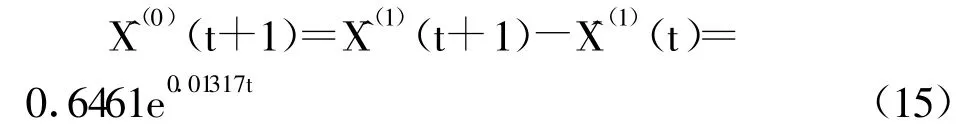
灰色GM(1,1)模型預測值與監測值比較見表2。

4.2 趨勢曲線模型

在建立趨勢曲線模型過程中,使用等維新息建模法[16],即采取增加新信息和去掉老信息同時進行的方式建模,使數列維數保持不變。如對X(1)建立模型預測x(1)(n+1)后,對X(1)進行等維新息處理后得到新數列X(1)=(x(1)(2),x(1)(3),…,x(1)(n),x(1)(n+1)),再用此數列建模預測x(1)(n+2),以此類推。趨勢曲線預測值和監測值對比見表3。

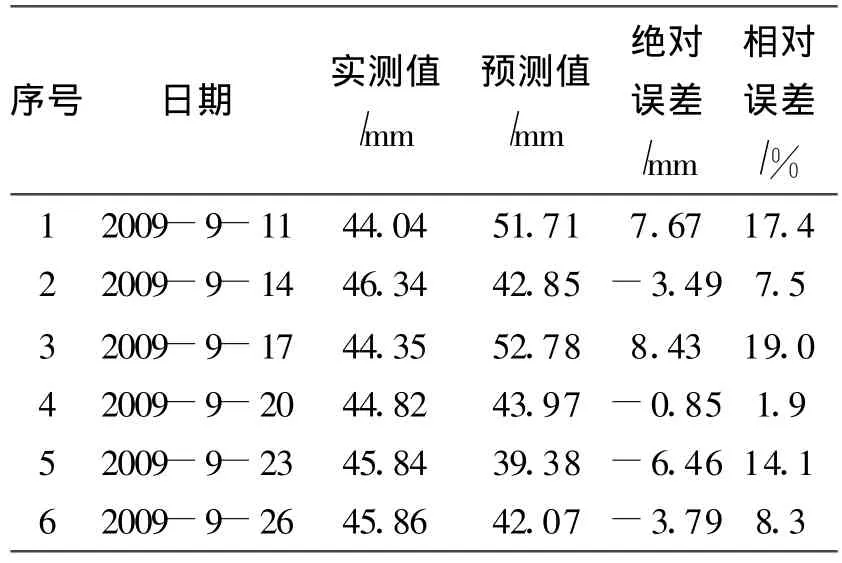
表3 趨曲線預測模型預測值與監測值比較Tab.3 Comparison between monitoring values and predicted values of trend curve prediction model

4.3 趨勢曲線-自記憶模型

建立趨勢曲線-自記憶模型過程時,取回溯階p=5(根據擬合情況通過試算法確定),在建模過程中同樣采取等維信息建模方法,可獲得位移預測方程為

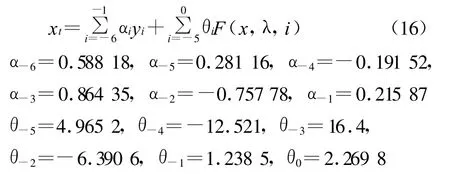
用上述建立的自記憶模型對表1中2009年6月13日到2009年9月8日的位移監測數據進行擬合計算,并對2009年9月11日到2009年9月26日的監測數據進行預測檢驗。趨勢曲線-自記憶模型預測值與監測值比較見表4。

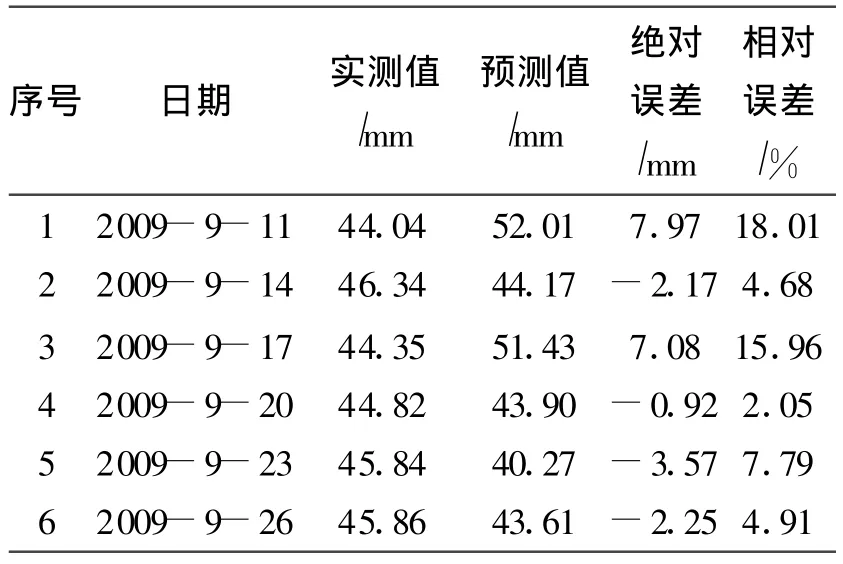
表4 趨勢曲線-自記憶模型預測值與監測值比較Tab.4 Comparison between monitoring values and predicted values of the trend curve-self-memory model

5 基坑位移預測對比分析

分析三種模型擬合和預測計算結果可知,使用GM(1,1)預測模型時,參與擬合計算的三十個樣本擬合相對誤差范圍為0.39%～19.26%,平均相對誤差為6.27%。預測計算結果中,相對誤差范圍為 13.3%～20.6%,平均相對誤差為18.47%。使用趨勢曲線預測模型時,擬合計算的相對誤差范圍為0.06%～9.99%,平均相對誤差為3.23%。預測計算結果中,相對誤差范圍為1.9%～19.0%,平均相對誤差為11.38%。使用趨勢曲線-自記憶模型時,擬合計算的相對誤差范圍為0.01%～7.51%,平均相對誤差為2.99%。預測計算結果中,相對誤差范圍為2.05%～18.01%,平均相對誤差為8.9%。

6 結論

1)三種預測模型中,灰色GM(1,1)模型預測精度較低,趨勢曲線模型相對較高,本文提出的趨勢曲線-自記憶模型預測精度最高。

2)趨勢曲線-自記憶模型利用多個歷史資料提供的記憶信息,某個監測值出現一定誤差對擬合和預測整體影響較小,提高了預測穩定性。

[1] 廖展宇,李英,晏鄂川,等.非等間隔時序灰色模型的深基坑變形預測研究[J] .合肥工業大學學報(自然科學版),2009,32(10):1521-1525.

[2] 莊妍,陳曉斌.GM(1,1)模型基坑結構變形預測應用研究[J] .廣州建筑,2009,6(12):26-30.

[3] 李磊,姜志強.深基坑支護結構位移的非等步長灰色模型預測[J] .勘察科學技術,2001(5):16-19.

[4] 李祥新,俞進萍.錨桿圍護結構的深基坑開挖中側向位移的預測控制[J] .探礦工程,2002(4):3-6.

[5] 陳記,韋立德.RBF網絡在基坑支護水平變形預測中的應用[J] .廣西工學院學報,2005,16(1):12-15.

[6] 王旭東,趙建平,余闖,等.人工神經網絡在深基坑變形預測中的應用[J] .南京工業大學學報,2002,24(5):73-76.

[7] 韋立德,徐衛亞,蔣中明,等.基坑支護結構水平變形預測的遺傳神經網絡方法[J] .工程地質學報,2003,11(3):297-301.

[8] 李云璋,韓曉雷.深基坑支護結構位移的神經網絡預測[J] .水利與建筑工程學報,2006,4(4):22-25.

[9] 李愛國,袁寶遠,陳艷國,等 .灰色神經網絡在深基坑位移預測中的應用[J] .人民黃河(水利水電工程),2006,28(4):77-79.

[10] 李榮峰.地下水動態預測的自記憶性模型及其應用研究[J] .山西水利科技,2005(1):6-8.

[11h曹鴻興.動力系統自憶性原理─預報和計算應用[M] .北京:地質出版社,2002.

[12] 李榮峰.水文非線性時間序列分析的自記憶模型研究[D] .西安:西安理工大學,2005.

[13] 左秀霞,王 偉,張偉葦.多項式趨勢曲線預測模型及軟件設計[J] .長江大學學報(自然科學版),2004,1(1):10-13.

[14] 李均立.GM(1,1)模型與趨勢曲線的組合預測方法在橡膠產量預測中的應用[J] .熱帶農業科學,1997,2(2):9-13.

[15] 謝成立,劉磊.灰色-趨勢曲線組合預測模型在港口吞吐量預測中的應用[J] .中國水運,2006,6(12):226-227.

[16] 易德生,郭 萍.灰色理論與方法[M] .北京:石油工業出版社,1992.