不允許賣空條件下不相關資產的實證分析

靳海娟，張作泉

（1.長治學院 數學系，山西 長治046000；2.北京交通大學 數學系，北京100044）

不允許賣空條件下不相關資產的實證分析

靳海娟1，張作泉2

（1.長治學院 數學系，山西 長治046000；2.北京交通大學 數學系，北京100044）

本文以選取的股票樣本為依據，把傳統的Markowitz模型和不允許賣空條件下不相關資產模型進行比較，通過相關數據的計算，證明了在相同收益的條件下，不相關資產模型能產生更小的風險，體現了不相關模型的優越性。因此，在實踐中可以有效的指導投資者的投資行為。

投資組合；不允許賣空；允許賣空；不相關資產；實證分析

1952年，Markowitz發表了一篇題為“投資組合選擇”的論文[1]，這個奠基性的工作對于金融學的發展所產生的影響是十分巨大和深遠的。但是，Markowitz的理論并沒有考慮投資比例系數的符號問題,由于負的投資比例系數意味著賣空相應的證券,而賣空程序在某些場合是很難實現的,所以研究不允許賣空條件下的資產組合理論有其實際意義。

本文引用了改進的不允許賣空條件下不相關資產的投資模型，并以深圳股市上選取的樣本為依據驗證了不存在無風險資產的情況下，改進的不允許賣空條件下不相關資產投資模型的可行性,并把其與傳統的Markowitz不相關資產模型進行了對比研究，獲得了更精確、更貼近實際、更有效的結果,從而能夠指導投資者的投資行為。

本文研究的是無摩擦的情況，然而，在考慮了部分摩擦因素(如帶交易費,稅收等等)后，不允許賣空時證券組合有效前沿的分析表達式也應該可以相應的得到。這個問題有待讀者考證。

一、Markowitz模型及不相關條件下的表示

當市場無摩擦且允許賣空時，標準的Markowitz均值方差模型：

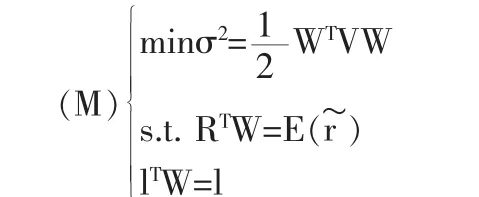
Merton[2]給出了模型（M）的有效投資組合及有效前沿的解析表達式：

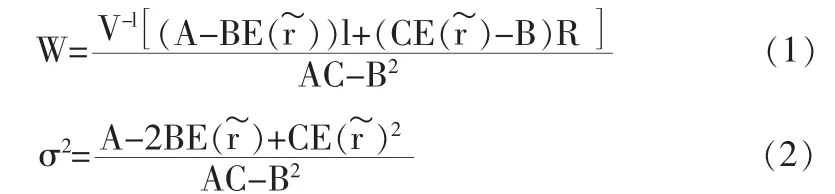
故式（1）可表示為：

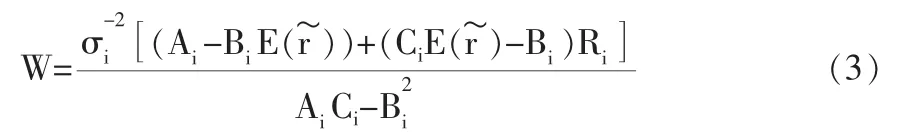
二、改進的不允許賣空條件下不相關資產的投資模型

當不考慮交易費且不允許賣空時,最優投資組合選擇模型（M）就可等價地寫成（M1）。

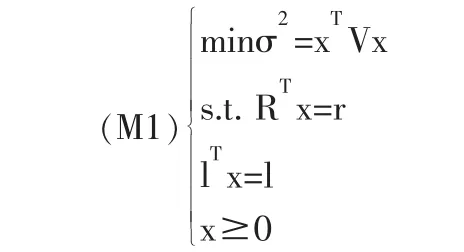
其中R=（R1，R2，…，Rn）為n種資產的期望收益率向量，r為給定的期望投資組合收益率，V=（σij）n×n是n種資產收益率的協方差距陣（假定為正定），l=（l，l，…，l）T是n維單位向量，x=（x1，x2，…，xn）T為投資組合（投資比例向量）。

模型 （M1）引起了眾多學者的廣泛重視。例如，Ross，Dybvig，Szego，楊德權等研究了有效投資組合的性質以及有效前沿的特征和解析表達式的確定方法,Markowitz提出了有效前沿的臨界線算法,唐小我等提出了參數單純形法。

此時最優投資組合選擇模型成為：

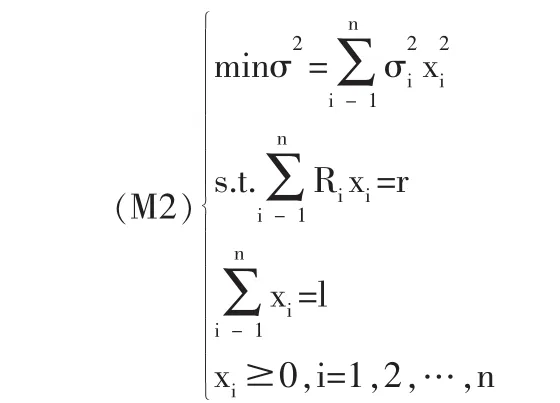
以下不妨假定記R1＜R2＜…＜Rn，記

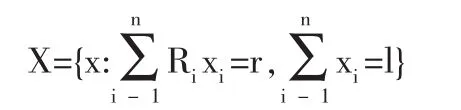
定理1[3]：當di-l燮r燮di（i=1，2，…，n-1）時，模型（M2）的最優投資組合為

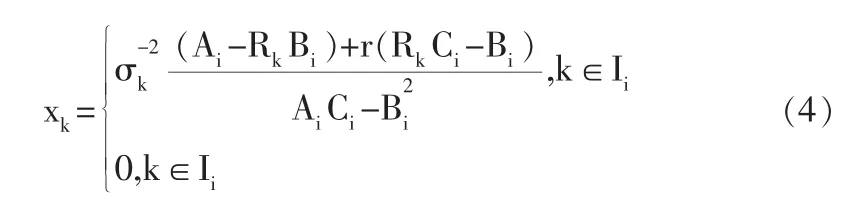
定理2[3]：模型（M2）的有效前沿是

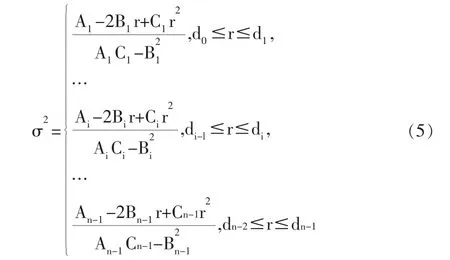
三、樣本股的確定及計算結果

對于不允許賣空條件下不相關資產的投資組合，我們用實例來驗證一下不存在無風險資產情況下的情形。

（一）樣本股的確定

我們從深圳證券市場上的500多只股票中,按照行業代表性、流通市值規模、交易活躍程度、上市公司財務狀況和經營業績以及地區代表性等原則,優先從股本規模大、成長性較好的個股中選取了從2002年1月11日至2004年4月2日,約2年的周收盤數據作為本文的研究樣本[4]。

為了研究方便我們做以下計算：

1.股票周收益率的計算：

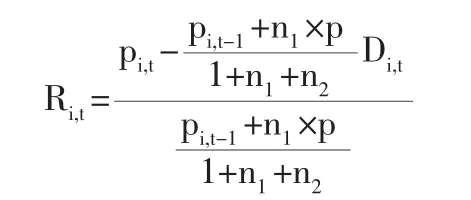
上式中，Ri,t為第i只股票第 t周的收益率；pi,t，pi,t-1分別為第i只股票在t，t-1周的價格；Di,t為第i只股票在第t周收取的現金股息；p為配股價；n1為配股比例；n2為送股比例。

2.第i只股票在這段時間中的平均周收益率為：

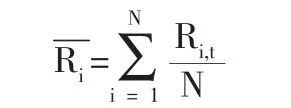
3.證券組合的平均周收益率和標準差公式為：

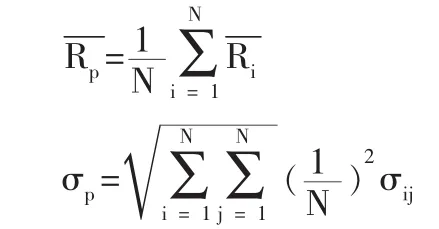
經過計算，得到各股的平均周收益率和標準差以及方差。根據平均周收益率大小，對這6只樣本股進行從小到大的排序，見表1。

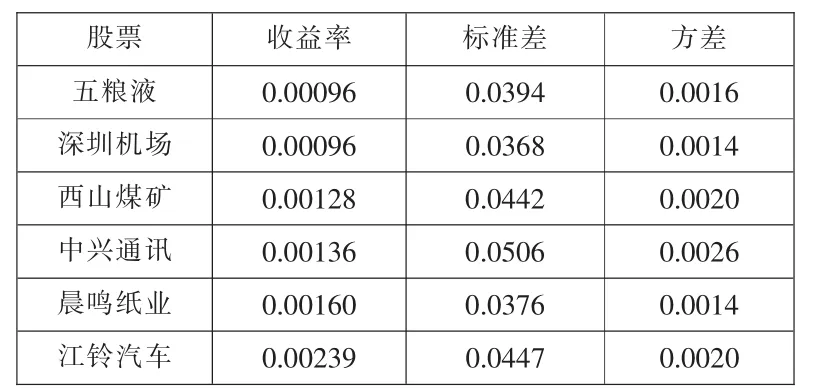
表1 ：樣本股的平均收益率和標準差

（二）計算結果

由于我們選取的樣本相互之間是不相關的,因此它們的協方差矩陣為對角矩陣,由表1我們可以得出所選取樣本的協方差矩陣：

它的逆矩陣為：

且有

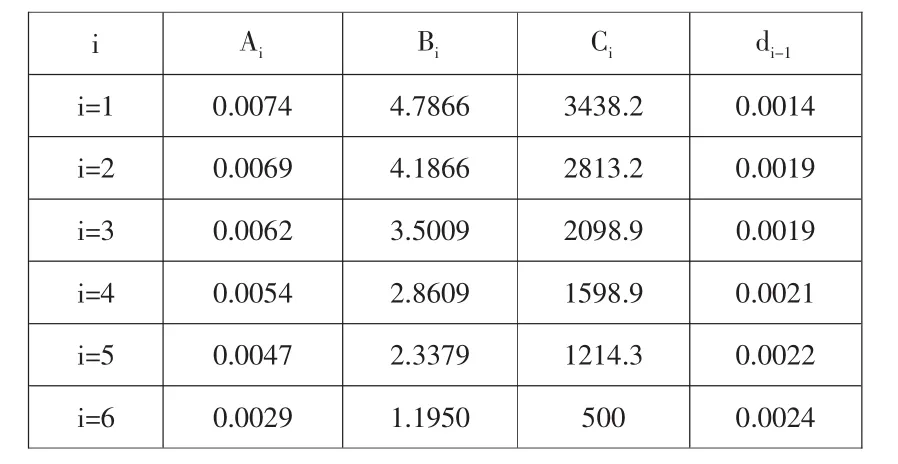
表2 ：各數值的計算結果

1.新模型的結果

用上面已經求得的數據我們來驗證第4章中新建的不允許賣空條件下不相關資產模型。先把數據代入（4）式，并利用風險的計算公式，我們得到了以下數據：

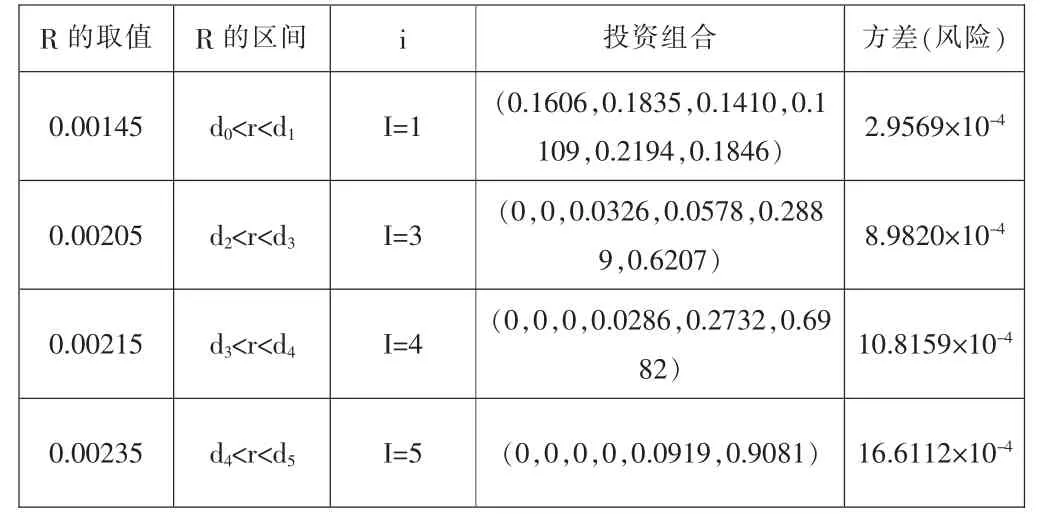
表3 ：模型（M2）的投資組合及風險的取值

2.Markowitz不相關資產模型的結果

同上面一樣，把表格2中求得的數據代入（3）式，并運用風險的計算公式得到了以下結果：

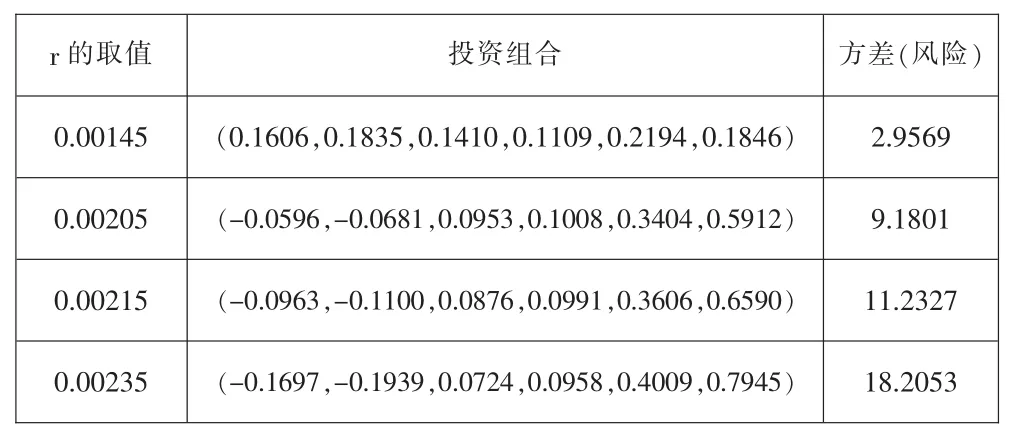
表4 ：Markowitz不相關資產模型下投資組合及風險的取值

四、結論

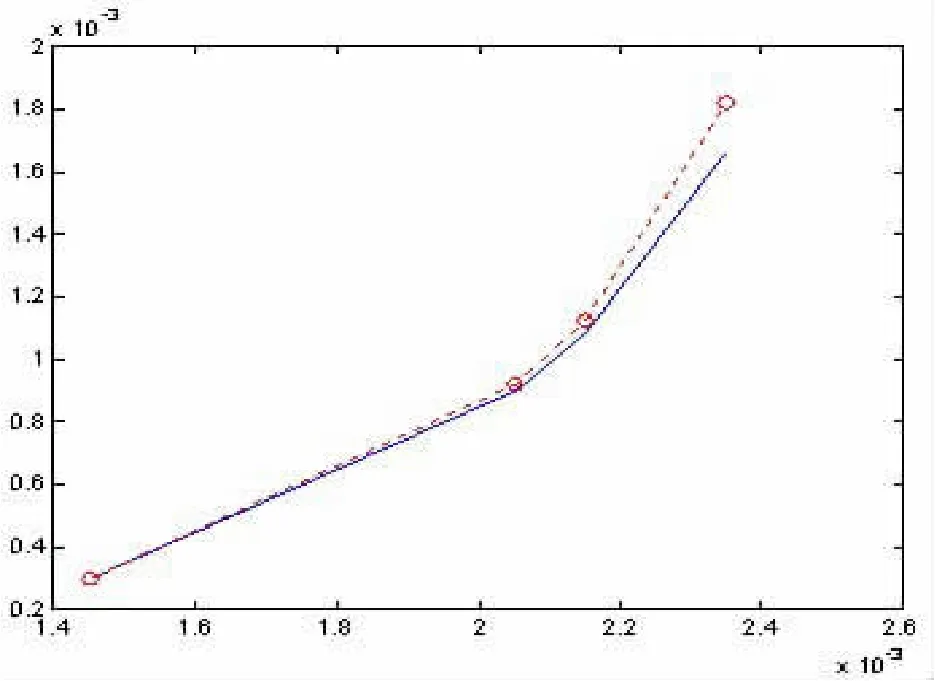
圖1 兩個模型風險的比較

從上圖中風險的比較以及前一部分的計算結果中，我們可以得到以下結論：

1.我們從表3、表4的數據結果可以看出該模型的可行性及正確性。表3中投資比例的取值均為正數，且每組之和均為1。這驗證了不允許賣空的條件：lTx=1及x叟0。

表4中投資比例的取值中有負數出現，這也符合Markowitz不相關資產模型中允許賣空的假設，同時也滿足lTW=1。因此,我們選取的模型是正確且可行的。

2.在收益率的取值相同的條件下,當分別運用（3）、（4）式求出投資組合后，從表中我們可以看出在收益率相同的前提下,改進的不允許賣空條件下不相關資產投資模型比傳統的Markowitz不相關資產模型產生的風險要小。這就說明,新的模型比傳統的Markowitz不相關資產模型更有優越性。

3.從表3、表4的結果還可以看出：這一投資組合所產生的風險都非常小。這說明，不相關資產組合能產生更小的風險。也就是說，在實際操作中，投資者應當盡可能選取那些不同行業、不同種類的股票組合投資,這樣相關系數低，有利于分散風險。[5]

致謝

在本文完成之際特別要感謝的是北京交通大學的張作泉教授。在撰寫本文的過程中，他給予了極大的幫助和指導，在此表示衷心的感謝。

[1]Markowitz H.Portfolio selection[J].The Journal of Finance,1952,7(1): 77-91.

[2]Merton.An analytic derivation of the efficient frontier[J].Journal of Finance and Quantitative Analysis9,1972.1851-1872.

[3]李仲飛,汪壽陽.投資組合優化與無套利分析[M].北京:科學出版社, 2001,(5):73-76.

[4]陳劍利,諸葛莉,周明華.馬克維茲模型在深圳股市應用中的實證研究[J].浙江工業大學學報,2005,(4):471-473.

[5]孫忠艷.分散化投資規模及風險資產比例選擇的實證研究[J].重慶工商大學學報(社會科學版),2003,20(3):18-20.