一類二階非線性泛函微分方程的振動性

張 平，周軒偉

(溫州大學數學與信息科學學院，浙江溫州 325035)

一類二階非線性泛函微分方程的振動性

張 平，周軒偉

(溫州大學數學與信息科學學院，浙江溫州 325035)

研究了一類二階非線性泛函微分方程的振動性，建立了4個新的振動定理，并給出了其應用.推廣了有關文獻中的部分結果.

泛函微分方程；非線性；振動性；漸進性

泛函微分方程在量子物理、工程力學、控制論、經濟與金融等學科中的應用非常廣泛，已成為研究的熱點課題之一.目前，對于泛函微分方程振動性的研究已取得了大量的成果.例如，文獻[1]研究了一類二階線性微分方程的振動性；文獻[2-3]研究了一類二階非線性微分方程的振動性；文獻[4-5]研究了一類二階非線性阻尼微分方程的振動性；文獻[6]研究了一類二階非線性攝動微分方程的振動性.本文的主要內容是研究一類非線性泛函微分方程

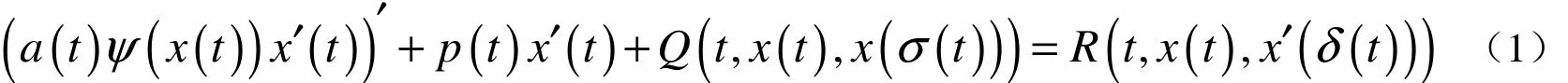
的振動性質.文獻[7-8]已給出了該方程的振動準則，本文在此基礎上，建立了關于該方程的4個新的振動定理，推廣了文獻[5-6]中的部分結果.

1 預備知識

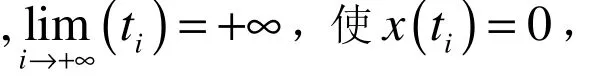
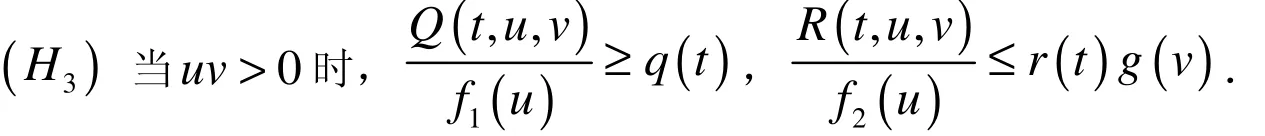
2 主要結果

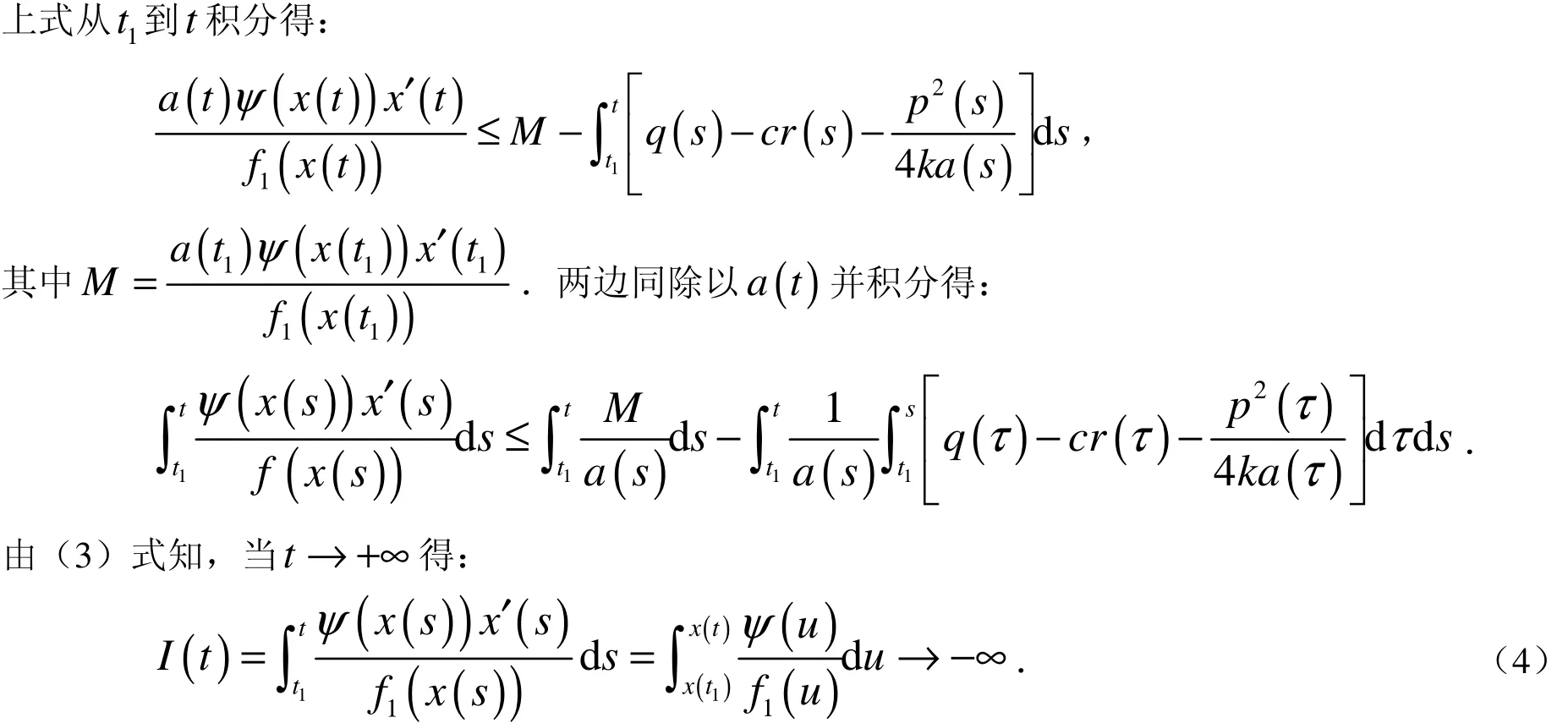
類似地可以證明，當t≥t1時，x(t)<0的情況.

注1：定理1推廣了文獻[5]中的定理4.

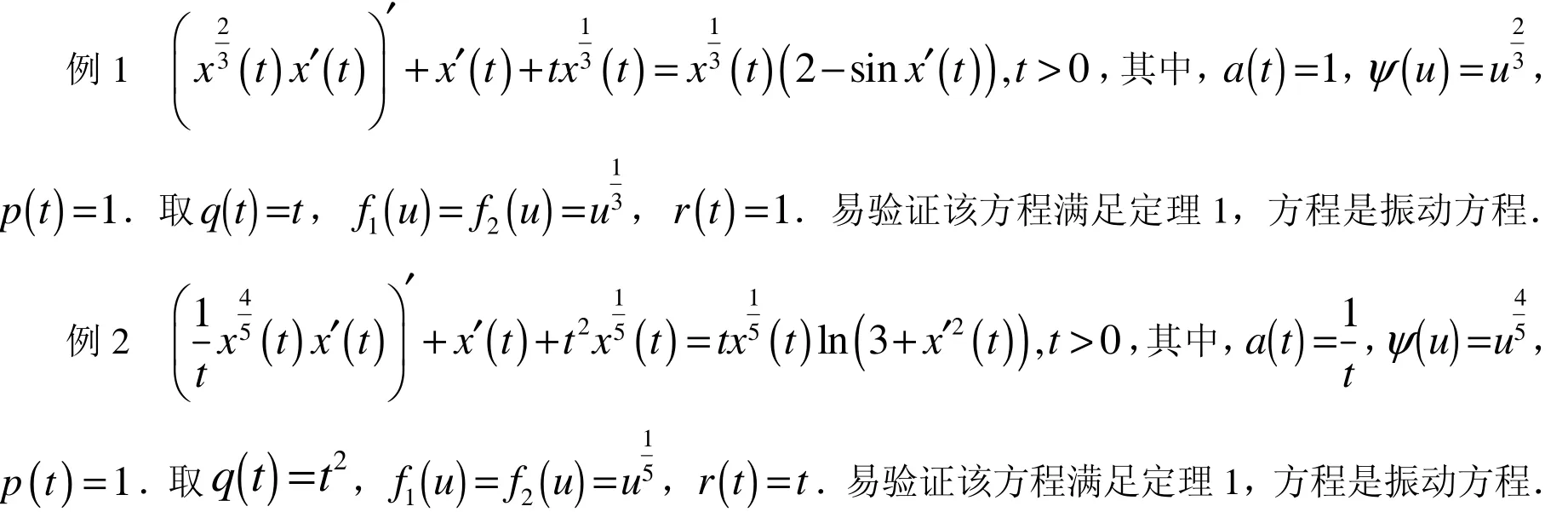
下面從方程解的漸近性討論方程的振動性質.

為了從解的漸近狀態著手討論方程（1）的振動性，將方程（1）的所有正則解分為以下4類：

[1]Wintner A. A criterion of oscillatory stability [J]. Quart Appl Math, 1949, 7: 115-117.

[2]Cecchi M, Marini M. Oscillatory behavior of a second order functional differential equation [J]. Rocky Mount J Math, 1992, 22: 1259-1276.

[3]Rogovchenko Y V. On oscillation of a second order linear delay differential equations [J]. Funkcial Ekvac, 2000, 3: 1-29.

[4]張全信, 燕居讓. 一類二階非線性阻尼微分方程的振動性[J]. 系統科學與數學, 2004, 24(3): 296-302.

[5]張全信, 燕居讓. 一類二階非線性阻尼微分方程的振動性質[J]. 純粹數學與應用數學, 2008, 24(4): 646-653.

[6]張全信, 燕居讓. 一類二階非線性攝動微分方程的振動性[J]. 濱州師專學報, 2003, 19(4): 1-6.

[7]高麗, 張全信, 燕居讓. 一類二階非線性泛函微分方程的振動性質[J]. 山西大學學報: 自然科學版, 2008, 31(1): 1-6.

[8]張吉慶, 黃利國. 二階非線性泛函微分方程的振動性質[J]. 數學的實踐與認識, 2008, 38(10): 128-131.

Oscillation of A Class of Second Order Nonlinear Functional Differential Equations

ZHANG Ping, ZHOU Xuanwei
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

Oscillation of a class of second order nonlinear functional differential equations was studied to build four new oscillation theorems. Then the theorems’ applications were given to further extend some results in the relevant documents.

Functional Differential Equation; Non-linearity; Oscillation; Asymptotic Behavior

(編輯：王一芳)

O177.91

A

1674-3563(2011)01-0009-08

10.3875/j.issn.1674-3563.2011.01.002 本文的PDF文件可以從xuebao.wzu.edu.cn獲得

2010-06-05

張平(1987- )，男，山東萊蕪人，碩士研究生，研究方向：多目標規劃，群體決策