含大彈性內齒圈行星傳動系統的動態特性分析

段福海 余 捷 林定笑 陳 栩

福建工程學院,福州,350108

含大彈性內齒圈行星傳動系統的動態特性分析

段福海 余 捷 林定笑 陳 栩

福建工程學院,福州,350108

為了深入了解引入大彈性內齒圈后行星傳動系統的動力學特性,建立了行星齒輪扭轉動力學模型,結合實例,采用數值仿真法對模型進行了求解,分析了嚙合剛度對系統嚙合動載荷的影響,并基于數值分析結論進行了實驗研究。數值仿真與實驗研究結果表明:嚙合剛度對含大彈性內齒圈的行星傳動系統的嚙合動載荷有較大影響,當內外嚙合剛度值相差較大時,系統嚙合動載荷較大;大彈性內齒圈的引入在很大程度上增大了太陽輪與行星輪的嚙合動載荷,同時使行星輪與內齒圈的嚙合動載荷有所減小;降低太陽輪與行星輪的嚙合剛度有助于減小其嚙合動載荷。在行星齒輪傳動系統中,合理地選擇構件參數可顯著減小系統的嚙合動載荷,從而有效降低系統的振動和噪聲。

行星齒輪;動載荷;嚙合剛度;大彈性內齒圈

0 引言

行星齒輪的多路徑功率分流傳動特性使其結構緊湊、功率密度大,因而在汽車、航空以及機電產品領域得到了廣泛的應用。近年來,人們通過進一步減小行星傳動裝置的體積和質量以提高其功率密度,所采取的方法主要有:采用更多的行星輪來分擔載荷;設法減小內齒圈的輪緣厚度或采用低密度的聚合物基復合材料齒輪來替換部分鋼齒輪。采用薄壁鋼或聚合物基復合材料的內齒圈,不但可減輕傳動系統的質量,而且利用內齒圈的大彈性變形能夠最大限度地降低內齒圈輪齒誤差、轉臂誤差以及各行星輪安裝誤差對系統均載性的影響[1-2]。另外,由于內齒圈直接與箱體相連,其所受動載荷對箱體的振動影響較大,出于降低系統振動和噪聲的目的,設計者試探著采用大彈性內齒圈替換傳統的剛性內齒圈來減小內齒圈與行星輪的嚙合動載荷。雖然國內外學者對行星齒輪動態特性進行了大量的研究[3-6],然而,有關大彈性內齒圈的引入對行星傳動系統的動態特性有何影響、如何配置系統參數才能獲得較佳的動態特性的研究報道還鮮見于文獻。為了深入了解大彈性內齒圈對行星傳動系統動態特性的影響,筆者建立了行星傳動的扭轉動力學模型和實驗模型,結合實例,對多種嚙合剛度組合的行星傳動系統進行了數值仿真和實驗研究,分析了嚙合剛度對系統動態特性的影響。

1 動力學模型

圖1為具有n個行星輪的行星傳動扭轉動力學模型,模型中考慮系桿、內齒圈、太陽輪以及行星輪的扭轉振動,取逆時針方向為正。規定系桿、內齒圈、太陽輪和行星輪的下標依次為c、r、s和p,第j個行星輪的下標為p j;θi(i=c,r,s,p1,p2,…,p n)為第i個構件繞其回轉中心的角位移;Ri為各構件的基圓半徑(Rc為各行星輪中心所在圓的回轉半徑);Ti為各構件上的扭矩;Ii為第i個構件繞其回轉中心的轉動慣量;系桿的等效轉動慣量I ce=I c+nm p R2c,其中,m p為行星輪的質量;k s j、k r j分別為第j個行星輪與太陽輪及內齒圈的時變嚙合剛度;c s j、c r j分別為第j個行星輪與太陽輪及內齒圈的嚙合阻尼;cc、cs、cr分別表示系桿、太陽輪、內齒圈的回轉阻尼;e s j、e r j分別為第j個行星輪與太陽輪及內齒圈的靜態嚙合誤差;αs、αr分別為太陽輪/行星輪、內齒圈/行星輪副的嚙合角;用廣義坐標ui表示回轉構件i的切向位移量 ,其中:uc=Rcθc,us=Rsθs,ur=Rrθr,uj=R p jθp j;用 mi表 示 廣 義 質 量, 其 中:m c=I ce/R2c,m s=I s/R2s,m r=I r/R2r,mj=I p j/R2pj;ko=ko u/R2o(o=c,r,s),ko u為第o個構件的回轉支承剛度。直齒輪副的嚙合輪齒對數隨齒輪的轉動發生單雙對的交替變化,該變化使其嚙合剛度發生周期性變化。為了便于進行數值分析,絕大多數齒輪動力學的研究均將嚙合剛度展開為Fourier級數,

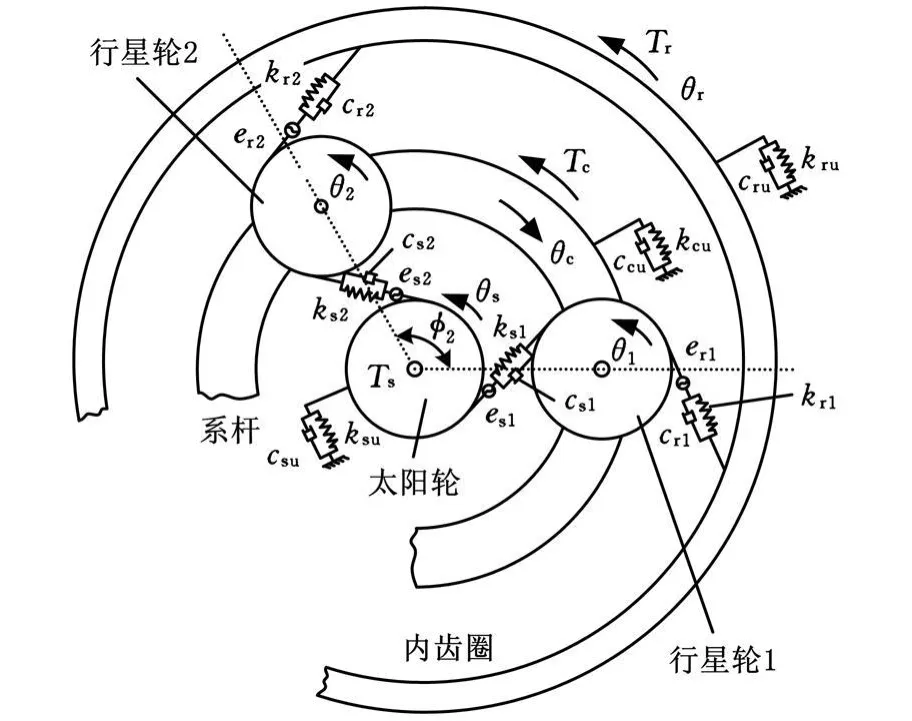
圖1 行星齒輪傳動動力學模型

公式如下:

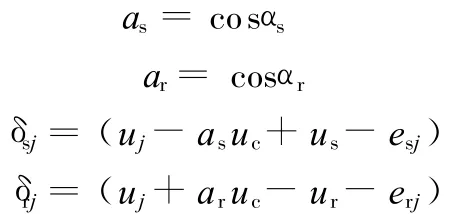
太陽輪與第n個行星輪的嚙合動載荷F s n、內齒圈與第n個行星輪的嚙合動載荷F r n為

式中,esn、ern分別表示太陽輪與第n個行星輪、內齒圈與第n個行星輪的靜態傳動誤差;ksn、krn分別為第n個行星輪與太陽輪及內齒圈的時變嚙合剛度。

2 數值分析結果

以某單級行星齒輪減速器為例進行數值分析和實驗研究,其具體參數為:太陽輪、行星輪、內齒圈的齒數分別為26、19、64,模數為 2mm,行星輪個數為3,壓力角為 22.4°,齒寬為 20mm,外嚙合重合度為1.5,內嚙合重合度為1.75。

設傳動中各行星輪的質量、轉動慣量均相同,太陽輪、內齒圈與每個行星輪的嚙合剛度均相等,太陽輪為輸入構件,系桿為輸出構件,內齒圈作為固定構件,通過減小內齒圈輪齒有效寬度或采用聚合物基復合材料內齒圈來降低內齒圈-行星輪的嚙合剛度。采用有限元模型,按照多嚙合點計算法,求出輪齒上20個嚙合點處的單齒剛度,然后按照嚙合點的對應關系求出結合輪齒的嚙合剛度,其時變嚙合剛度曲線如圖2所示,其中圖2a和圖2b分別為剛性太陽輪-行星輪的嚙合剛度、剛性內齒圈-行星輪的嚙合剛度,圖2c為大彈性內齒圈-行星輪的嚙合剛度。從圖2可以看出,當采用大彈性內齒圈后,內嚙合齒輪副的時變嚙合剛度發生了較大的變化。

在輸入軸轉速為2500r/min、負載為35N?m的工況下,對三種不同的太陽輪-行星輪嚙合剛度(平均嚙合剛度)的大彈性內齒圈行星傳動系統的嚙合動載荷進行計算,其中剛性齒輪副的相對嚙合阻尼系數為0.15,含大彈性齒輪副的嚙合阻尼系數為0.3,齒輪副的靜態傳動誤差幅值為20μm,采用變步長 Runge-Kutta法對式(3)和式(4)進行數值求解,系統動載荷計算結果如圖3和圖4所示。

從圖3可以看出,在含有大彈性內齒圈的行星傳動系統中,內齒圈與行星輪的平均嚙合剛度為=0.25×108N/m,當太陽輪-行星輪嚙合剛度較低時,二者的嚙合動載荷小,不會發生脫齒現象。隨著太陽輪-行星輪嚙合剛度的增大,太陽輪-行星輪的嚙合動載荷急劇增大,發生嚴重的脫齒現象。當嚙合剛度較大時,太陽輪-行星輪的嚙合動載荷急劇增大,同時出現峰值稍小的動載荷,該動載荷的出現使齒輪在相同周期內承受沖擊的次數增加一倍。從圖4可以看出,當太陽輪-行星輪嚙合剛度較低時,嚙合剛度對內齒圈-行星輪的嚙合動載荷影響不大,然而當太陽輪與行星輪嚙合剛度較高時,內齒圈-行星輪的嚙合動載荷波動次數增大一倍。動載荷波動次數增大一倍表現為嚙合頻譜中齒輪嚙合二倍頻的出現。

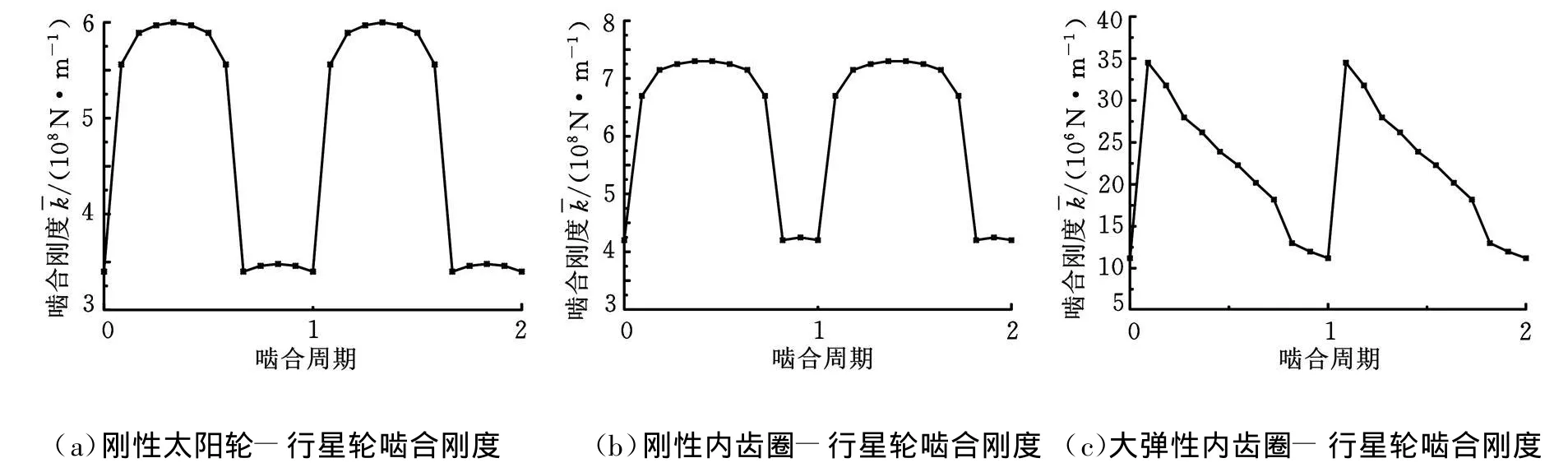
圖2 齒輪副嚙合剛度

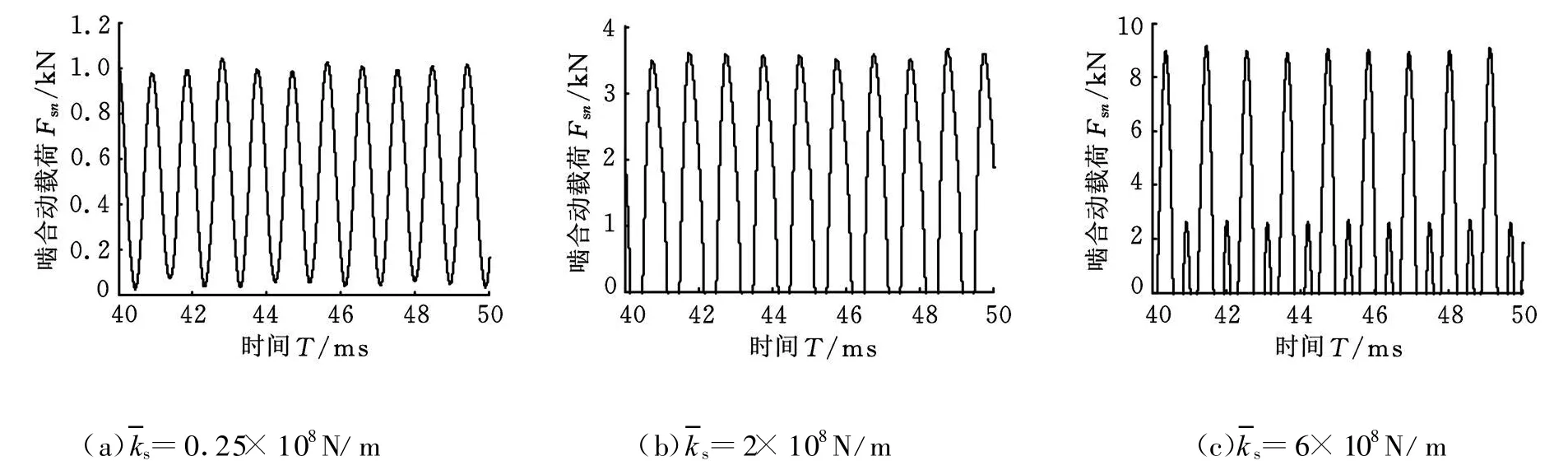
圖3 太陽輪-行星輪的平均嚙合剛度對太陽輪-行星輪嚙合動載荷的影響

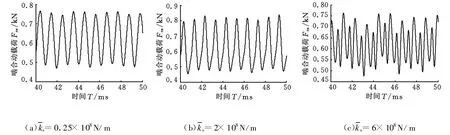
圖4 對內齒圈-行星輪嚙合動載荷的影響

為了分析內齒圈-行星輪嚙合剛度對含有大彈性內齒圈的行星傳動系統嚙合動載荷的影響,對三種行星傳動系統的嚙合動載荷進行了計算,此時太陽輪-行星輪的平均嚙合剛度為=4.85×108N/m,計算結果如圖5和圖 6所示。從圖5可以看出,太陽輪-行星輪嚙合動載荷隨著內齒圈-行星輪嚙合剛度的增大而減小。從圖6中可以看出,內齒圈-行星輪嚙合動載荷隨著內齒圈-行星輪嚙合剛度的增大而增大,當內齒圈-行星輪嚙合剛度超過一定值后,內齒圈-行星輪的嚙合輪齒開始出現脫齒現象。從內齒圈-行星輪的嚙合剛度對系統嚙合動載荷的影響來看,增加其剛度使太陽輪-行星輪嚙合動載荷產生較大幅度的減小,同時使內齒圈-行星輪嚙合動載荷有所增大,這就要求在可靠性設計中應考慮系統嚙合剛度優化匹配的問題,使各構件的可靠性盡量接近。

從上述分析來看,嚙合剛度對含有大彈性內齒圈行星傳動系統的嚙合動載荷產生較大影響,當內外嚙合剛度值相差較大時,會導致系統嚙合動載荷較大。在含有大彈性內齒圈的系統中,降低太陽輪-行星輪的嚙合剛度有助于減小系統的嚙合動載荷;增大大彈性內齒圈-行星輪的嚙合剛度可有效地降低太陽輪-行星輪的嚙合動載荷。

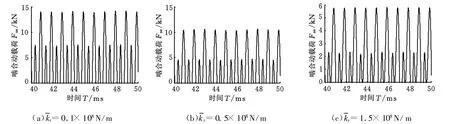
圖5 對太陽輪-行星輪嚙合動載荷的影響

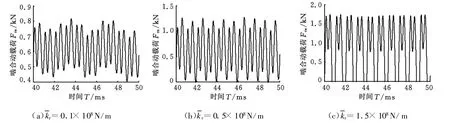
圖6 對內齒圈-行星輪嚙合動載荷的影響

3 實驗驗證

為了驗證上述數值分析的正確性,對剛性及大彈性內齒圈行星傳動系統進行了實驗研究,實驗裝置如圖7所示。實驗裝置主要由電機、變頻器、行星齒輪箱、磁粉加載器、聯軸器、加速度傳感器、電渦流傳感器、張力控制器等組成。

圖7 動態特性測試系統

為了盡量保持與上述數值計算結果一致,采用輸入軸轉速2500r/min、負載35N?m的工況進行測試。通過實驗發現:太陽輪支撐軸承上的振動能較好地反映太陽輪-行星輪的嚙合狀況,內齒圈上的振動能較好地反映內齒圈-行星輪的嚙合狀況,因而通過對其振動強度分析可以了解內外齒輪副的嚙合動載荷情況。分別對剛性、含大彈性內齒圈和基于數值仿真優化嚙合剛度后的三種行星傳動系統進行了實驗,采用頻譜響應來描述各系統的振動情況,其結果如圖8和圖9所示。

從圖8可以看出,引入大彈性內齒圈后太陽輪支撐軸承上嚙合基頻處的頻譜峰值高于剛性系統,且均出現嚙合二倍頻譜峰,這與數值分析結論一致。另外,根據圖3和圖4a的數值分析結論進行太陽輪-行星輪的嚙合剛度調整,即通過減小太陽輪輪齒寬度以獲得較小的太陽輪-行星輪的嚙合剛度,從圖8c中可以看出,在大彈性內齒圈行星傳動系統中減小太陽輪-行星輪的嚙合剛度可有效降低太陽輪支撐軸承上的振動強度,進而降低系統的振動和噪聲,提高太陽輪及其支撐軸承的可靠性。

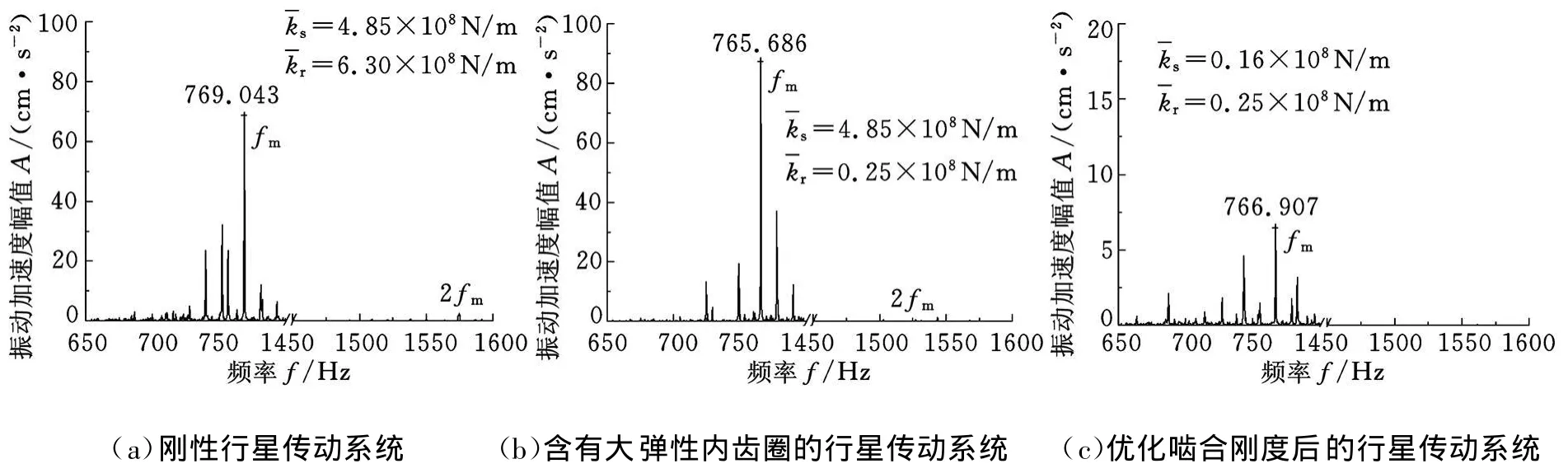
圖8 太陽輪支撐軸承上的振動頻譜

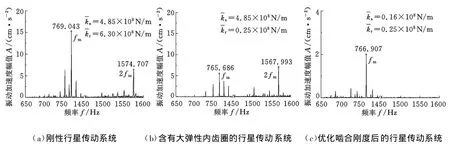
圖9 內齒圈上的振動頻譜

從圖9可以看出,與剛性行星傳動系統相比,大彈性內齒圈的引入在一定程度上降低了嚙合基頻處的振動強度,對嚙合二倍頻處的振動強度影響不大。通過降低太陽輪-行星輪的嚙合剛度可有效降低嚙合基頻處的振動強度,同時對嚙合二倍頻處的振動強度起到較好的抑制作用。另外,可以發現太陽輪-行星輪的嚙合對系統嚙合二倍頻的產生起較大作用。

4 結論

(1)嚙合剛度對含有大彈性內齒圈的行星傳動系統的嚙合動載荷產生較大影響,當內外嚙合剛度值相差較大時,系統嚙合動載荷較大。大彈性內齒圈的引入使太陽輪-行星輪的嚙合動載荷急劇增大,導致太陽輪、行星輪及其支撐軸承的壽命和可靠性降低。另外,大彈性內齒圈的引入在一定程度上降低了行星輪-內齒圈的嚙合動載荷,使系統的振動和噪聲有所減小。

(2)在滿足強度要求的前提下,可通過優化匹配系統嚙合剛度來減小大彈性內齒圈行星傳動系統的嚙合動載荷。可采用兩種嚙合剛度調整方法:一是通過減小太陽輪的齒寬來減小太陽輪-行星輪的嚙合剛度,減小太陽輪-行星輪的嚙合剛度可有效減小系統的嚙合動載荷;二是通過增大內齒圈齒寬或輪緣厚度來增大內齒圈-行星輪的嚙合剛度以減小太陽輪-行星輪的嚙合動載荷。

(3)太陽輪-行星輪的嚙合對行星傳動系統嚙合二倍頻的產生起較大作用,通過減小太陽輪-行星輪的嚙合剛度可有效減小嚙合二倍頻處的振動強度。

[1] Kahraman A,KharaziA A,Um rani M.A Deformab le Body Dynam ic Analysis of Planetary Gearswith Thin Rims[J].Journal o f Sound and Vibration,2003,262:752-768.

[2] W u X,Parker G.Vibration of Rings on a General Elastic Foundation[J].Journalof Sound and Vibration,2006,295:194-213.

[3] Yuksel C,Kahraman A.Dynam ic Tooth Loads o f Planetary Gear Sets Having Tooth ProfileWear[J].Mechanism and M achine Theory,2004,39:695-715.

[4] Inalop lat M,Kahraman A.A Theoretical and Experimental Investigation of Modulation Sidebands o f Planetary Gear Sets[J].Journal of Sound and V ibration,2009,323:677-696.

[5] Ambarisha V K,Parker R G.Nonlinear Dynam ics of Planetary Gears Using Analy tical and Finite Element M odels[J].Journal of Sound and Vibration,2007,302:577-595.

[6] BartelmusW,Zim roz R.Vibration Condition Monitoring of Planetary Gearbox Under Varying Ex ternal Load[J].Mechanical Systems and Single Processing,2009,23(1):246-257.

Dynam ic Characteristics of Planetary Gearsw ith Elastic Ring Gear

Duan Fuhai Yu Jie Lin Dingxiao Chen Xu
Fujian University of Technology,Fuzhou,350108

A torsional dynam icsmodelof planetary gears was developed to study the effects of elastic ring gear on its dynamics characteristics.Themodels were solved by using numericalmethods.Some experiments were taken based on numerical resu lts.The numerical and experim ental resu lts show that the mesh stiffness in fluences the dynam ic loads for planetary gear systems with elastic ring gear significantly,and high dynamic loads for system w ill yield as the difference between ex ternal and internalmesh stiffness becom es large,substituting elastic ring gear for rigid one can increase dynamic loads on sun-p lanetmesh m arkedly,how ever,reduce dynam ic loads on ring-p lanetmesh to certain extent.Sun-p lanet dynam ic load can be reduced by decreasing theirmesh stiffness.The system mesh dynamic loadsmay effectively be reduced by choosing system parameters properly in planetary gear system s with elastic ring gear.

p lanetary gear;dynamic load;mesh stiffness;elastic ring gear

TH 112

1004—132X(2011)04—0428—05

2009—11—02

福建省自然科學基金資助項目(2010J01269)

(編輯 王艷麗)

段福海,男,1979年生。福建工程學院機電及自動化工程系講師、博士。研究方向為機電傳動技術、車輛工程。發表論文20余篇。余 捷,男,1984年生。福建工程學院機電及自動化系助教。林定笑,男,1969年生。福建工程學院機電及自動化工程系副教授。陳 栩,男,1976年生。福建工程學院機電及自動化工程系講師。