V帶疲勞壽命最長的全局優化設計

張少軍 萬 中 劉光連

中南大學,長沙,410083

0 引言

V帶傳動具有結構簡單、運行平穩、低噪聲、能緩和載荷沖擊、傳遞功率較大、能實現過載保護、生產成本低以及制造和安裝容易等一系列優點,所以廣泛應用于各類機械中[1-2]。對V帶工作能力的考慮主要包括兩個方面,即V帶傳動能力和V帶的壽命。二者密切相關且相互矛盾,若提高V帶的傳動能力,則V帶的壽命就會降低;反之亦然[3]。從V帶傳動實際使用情況來看,對于長期連續運轉的V帶,壽命是主要要求;而間歇工作的V帶,傳動能力則上升為主要要求。如何根據所需傳遞功率、主動輪轉速等條件使設計出的V帶傳動系統中V帶疲勞壽命最長,這對于節約資源、降低成本、提高系統可靠性具有積極意義。

為了實現V帶傳動的優化設計,國內外學者進行了諸多研究。文獻[4-6]對已有理論和方法作了較系統和全面的闡述。此外,還有一些軟件公司開發了專門的V帶設計軟件(如Ciclo VBelt)。最近的研究成果可參看文獻[7-8]。文獻[7]用改進的遺傳算法對帶傳動多目標進行了優化,文獻[8]對V帶輪的疲勞壽命進行了優化。不過,在已有的文獻中,尚未見到關于V帶疲勞壽命最長的全局優化設計問題的討論,而是較多關注于對V帶傳動能力[9]、帶輪體積[10]等的優化,或僅限于對V帶疲勞壽命優化的原理性探討[11-12],或者對所建立的優化模型采用一些經典的局部優化算法(如罰函數方法)求解。本文在建立V帶疲勞壽命最長優化設計模型的基礎上,通過深入分析目標函數和約束條件的性質,在給定的設計條件下提出全局優化方法。

1 V帶疲勞壽命最長優化模型

假設V帶型號確定,小帶輪(即主動輪)轉速n1(r/min)和傳動比i給定,要通過選取設計變量V帶節線長(簡稱帶長)L(mm)、小帶輪直徑 d1(mm)和單根V帶所要傳遞的功率P(k W)來使得V帶疲勞壽命T(h)最長。

由實驗可知,V帶最大應力δmax與它的總循環次數N有如下關系：

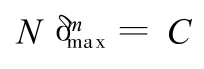
式中,C為實驗常數,由傳動帶的材質、結構和尺寸決定;m為曲線指數(一般為6～11)[11],當V帶型號確定且 N可能的變化范圍不是很大的情況下,可近似地視m為一恒定值(如 N為108～109時,m取11.1)[13]。

由上式出發,根據V帶傳動的應力分析[14],可推導出特定參數情況下單根V帶在兩輪間傳動時所能傳遞的最大功率P0為

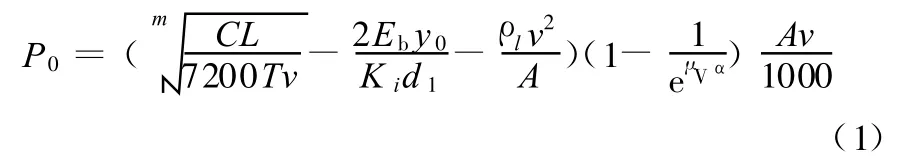
式中,v為帶速,m/s;Eb為V帶彎曲彈性模量,MPa;y0為V帶外層至中性層距離,mm;Ki為傳動比系數;ρl為V帶線質量,kg/m;A為V帶橫截面積,mm2;μV為V帶與帶輪槽間的當量摩擦因數;α為小帶輪包角,rad。

假設單根V帶所要傳遞的功率P在其所能傳遞的極限功率范圍內,由于V帶疲勞壽命隨傳動帶的初張力F 0增加而顯著降低[15-16],為保證所需傳遞的功率又不出現打滑現象,且V帶疲勞壽命T最長,這時需將初張力調整到剛好滿足所需傳遞功率要求,也即此時單根V帶所要傳遞的功率P就等于它所能傳遞的最大功率P 0。

設設計變量 x=(x1,x 2,x3)T=

根據實際生產工藝和工程要求,V帶傳動設計必須考慮基本約束條件如下：

(1)中心距設計約束：

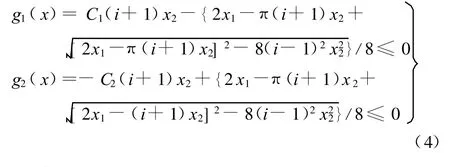
(2)V帶的帶速限制：

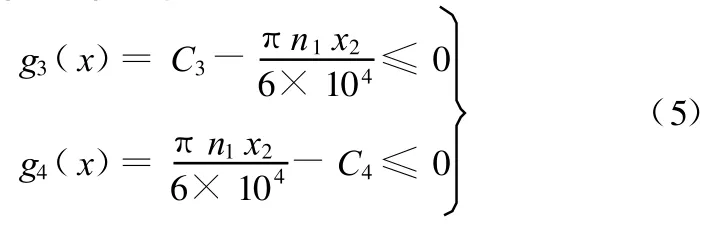
(3)單根V帶傳遞功率限制：

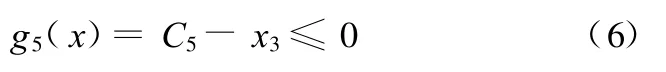
(4)小帶輪直徑設計約束：

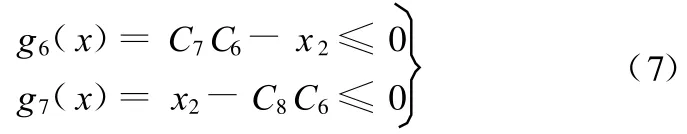
(5)V帶節線長設計約束：

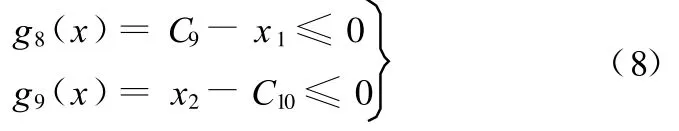
(6)小帶輪包角設計約束：

其中,C1～C12為約束條件中的常系數,具體數值見表1。

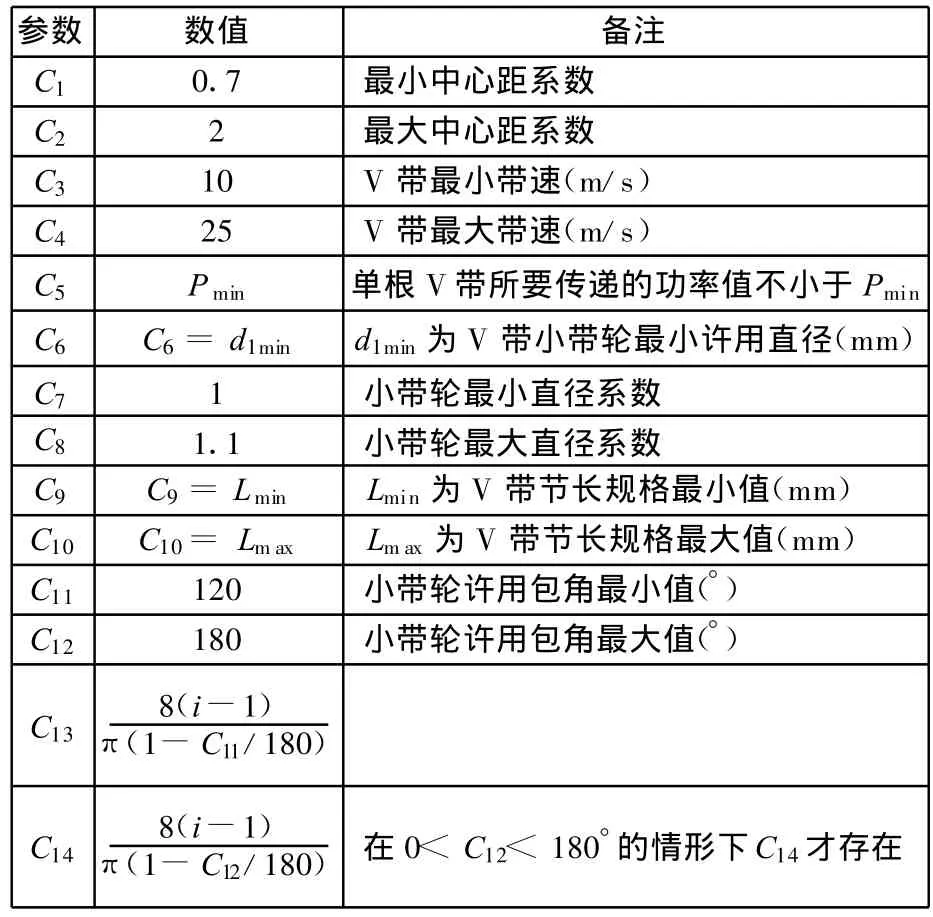
表1 V帶優化模型中的常系數列表

因此,V帶疲勞壽命最長優化設計模型為

以往的V帶傳動優化設計中,常常利用一些經典的算法(如罰函數方法)[17]求解式(10)。其主要缺陷在于：①沒有更深入地分析該問題目標函數的性質和可行域的結構,因而采用的算法未必是計算效率最高的;②如果式(10)不是凸規劃問題,采用任何經典的優化算法都不能從理論上保證所求得的解是該問題的全局最優解。本文的主要工作就是要在深入分析式(10)結構性質的基礎上,提出針對該問題的高效算法。

2 目標函數的性質和可行域的結構

為了設計最有效的求解上述優化問題(式(10))的算法,首先證明一下目標函數的一些結論。

定理1 目標函數T(x 1,x2,x3)關于第一個變量x1在區間(0,+∞)內單調遞增,關于第三個變量x3在區間(0,+∞)內單調遞減。

證明：目標函數T(x1,x2,x3)關于第三個變量x3在區間(0,+∞)內單調遞減是顯然的。由式(3)不難證明α關于變量x 1在區間(0,+∞)內的單調遞增。由式(2)也可證明目標函數T是關于α在區間(0,+∞)內的單調遞增函數。根據復合函數及其導數的性質,容易證明目標函數T關于變量x 1在區間(0,+∞)內單調遞增,因此定理的結論成立。

設單根V帶所要傳遞的功率不小于Pmin。由于x 3在優化模型中相對獨立,且T關于變量x 3在(0,+∞)內單調遞減,因此可首先取定 x3=P min,這樣模型中就只剩下 x1、x2兩個待設計變量。

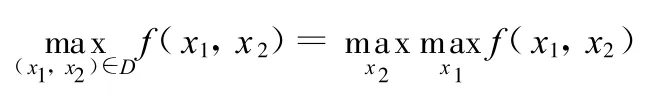
證明：首先

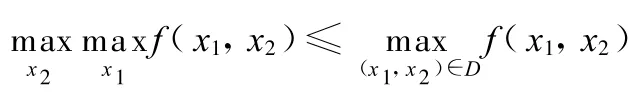
是顯然的,我們只要證明

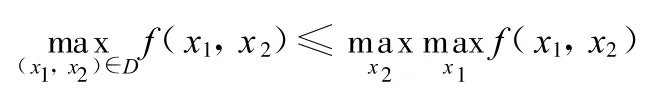
成立。

對任意給定的x2,令

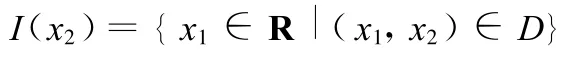
因為D是單連通的有界閉集,所以I(x2)是有界閉區間,記此區間的右端點為r(x2)。

因為f是D內的連續函數,且關于x1單調遞增,所以對任意點(x 1,x2)∈D,有

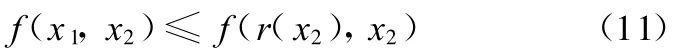
又記

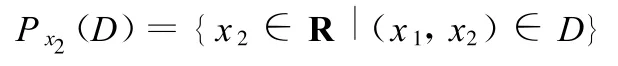
則集合P x2(D)是D在x 2軸上的投影。因為D是單連通有界閉集,所以Px2(D)是 x2軸上的有界閉區間。

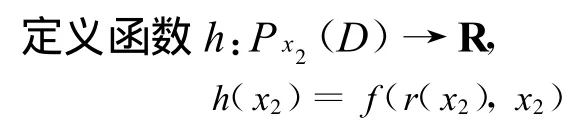
因為 f是D內的連續函數,所以 h是有界閉集P x2(D)上的連續函數,且存在最大值點x*2。

由式(11)和 h的定義知,對任意點(x1,x2)∈D,有

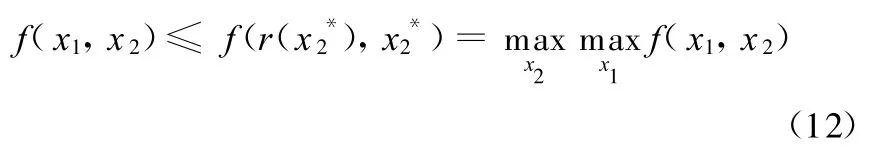
所以

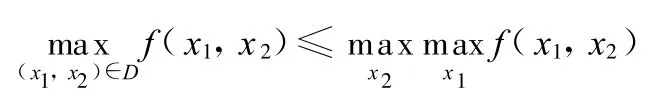
盡管優化模型(式(10))中的目標函數在區域R2

+內無界,但定理2對我們在下節提出求解式(10)的最有效的全局優化方法有很多幫助,因為后面我們將證明該問題的可行域是有界閉凸集。因此,根據定理2,我們能夠提出優化模型(式(10))的全局最優解滿足的條件。下面證明目標函數在一般情況下不是凹函數,從而原問題不能用凸規劃方法求解。因此可以肯定,以往研究工作中采用經典的局部優化算法不能從理論上保證求得的解是原問題的最優解。

定理3 目標函數T不是凹函數。

證明：事實上,若取定B1=711.017,B2=10.507,B3=94.157,B4=0.55×10-6,i=3.65,m=11,則當 x1=2000、x2=154時,T的 Hesstan陣

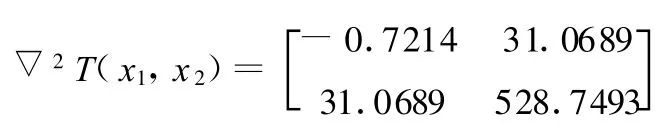
是不定矩陣。因此,目標函數一定不是凹函數(任何點處Hessian陣為負定矩陣)。

接下來,我們研究優化問題(式(10))的可行域結構。為此,我們把約束條件式(4)～式(9)作如下簡化：

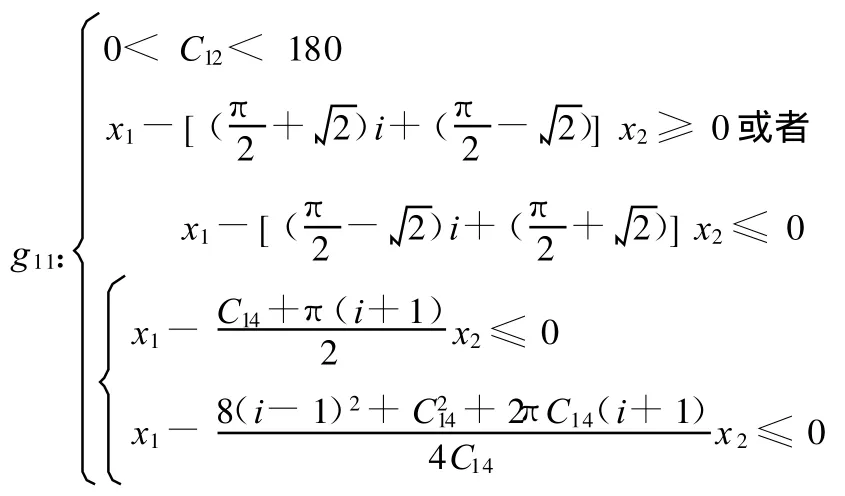
或取C12=180,此時由g1約束式和i≥1可知原g11約束恒成立。

將 g3、g4 、g6、g7 約束式合并為

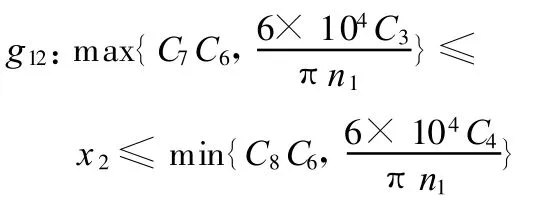
將g8、g9約束合并為

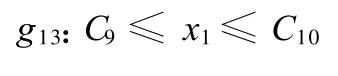
以上 g1、g2、g5 、g10、g11、g12 、g13 構成了總的約束條件,它們均為線性約束,因此我們可得如下結論：

定理4 優化模型的可行域Ix={(x1,x2)∈R2

+|(x1,x2)滿足條件式(4)～式(9)}是有界閉凸集(此時x3取為定值P min)。

3 全局優化算法

基于定理1、定理2和定理4,我們提出如下計算優化模型全局最優解的高效算法(我們稱之為最優值線段算法)：

(1)把式(10)(此時x3取為定值Pmin)中每一個約束條件歸為如下三類之一：①x1≤kx 2,k＞0;②x 1≥kx 2,k＞0;③a≤x1≤b,c≤x2≤d,a、b、c、d均為大于零的常數。

(2)取k1=min{k|k是第 ①類約束的斜率},k2=max{k|k是第②類約束的斜率}。一般地,k1≥k2。設直線x 1=k1 x2與直線x1=a交點的縱坐標為ea,與 x1=b交點的縱坐標為eb。直線x1=k2x2與直線x1=α交點的縱坐標為ga,與x1=b交點的縱坐標為g b。則

①當ea＞d時,問題無解;②當ea≤d且eb≥d時,可直接得到該問題的全局最優解x*=(x*1,x*2)=(k1 d,d);③當eb＜d且g b≥c時,則在直線段x 1=b,(max{c,eb}≤x 2≤min{d,gb})上尋找最優解,此時將x1=b代入到目標函數,則原優化問題可歸結為一元連續可微函數在有界閉區間上的全局優化問題,再利用有效的全局優化方法,如覆蓋法[18],就能得到原問題的全局最優解;④當gb＜c時,該問題無解。

4 設計實例

試以V帶疲勞壽命最長為目標設計一V帶傳動系統。其中主動輪轉速n1=1460r/min,傳動比i=3.65,用普通B型V帶傳動,其單根V帶傳遞功率P不小于P min=3.50k W。

查表[19]得普通 B型 V帶參數：ρl≈0.17kg/m,A=142.96mm2,y0=4.1212mm。Eb=55.7MPa,K i=1.1373,μV=0.51,C ≈1.8099×1014。優化模型中各系數值如表 2所示。

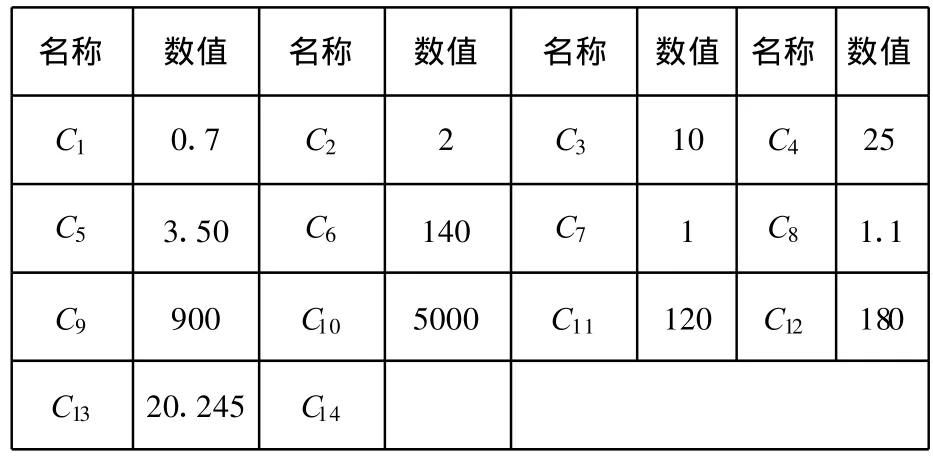
表2 設計實例的模型系數值列表

首先選定 x3=3.50kW。經計算得：B2=24.4824,B3=30.8592,B4=0.5312×10-6。

通過整理各約束條件得到總的可行域Ix為

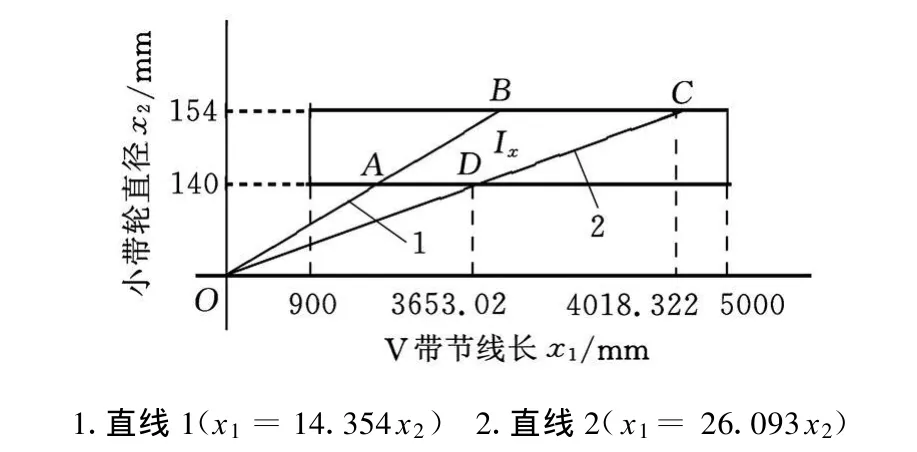
圖1 實例中可行域Ix的圖形

此優化問題可行域的特點符合最優值線段算法(2)中的情形 ②。由最優值線段算法可知,T(x)的全局最大值解必然就是圖1中的點C,即全局最優解x*=(4018.322,154,3.50)T。設此問題中m取值為11.0,則V帶疲勞壽命最長的全局最優值 Tmax≈61923h。

在已有的文獻中,尚未見到關于V帶疲勞壽命最長優化設計問題的具體研究,所以無從比較。但在文獻[20]中計算得到的普通B型V帶在額定功率工作時的預期疲勞壽命約為24 000h,遠低于本實例中得到的B型V帶疲勞壽命最長的全局最優值。這也反映了本文優化模型和優化方法的有效性。

工程實際中由于工作空間或機械整體尺寸的限制,有時還要求中心距a≤a max,其中a max為一常數,這相當于在原模型中增加約束條件：

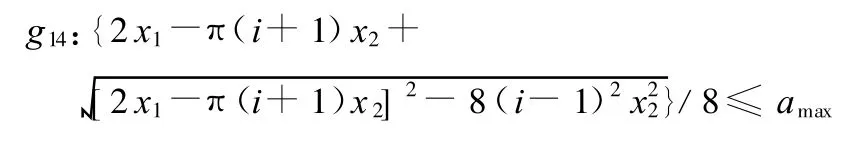
即

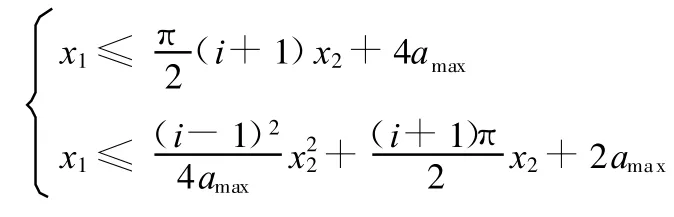
以上為一線性約束和非線性約束的組合。當曲線

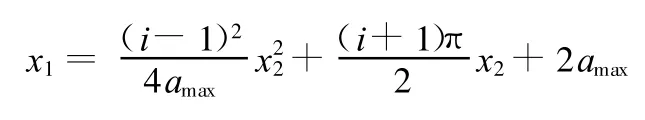
為可行域Ix沿坐標x 1增大方向一側的全部或部分邊界時,可行域就不一定是凸集。但此時并不妨礙上述最優值線段算法的使用。若可行域最右側邊界全部由該二次曲線組成,則可按最優值線段算法(2)中情形 ②的處理方法來計算最優解,最優解為

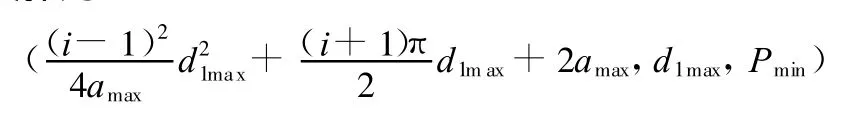
其中,d 1max為小帶輪直徑在可行域范圍內能取到的最大值。若可行域最右側邊界只是一部分由該二次曲線組成,則可按(2)中的情形 ③來計算。

5 結束語

本文建立了以V帶疲勞壽命最長為目標的優化設計模型。深入研究了該模型中目標函數的凸性、單調性等特性,證明了其可行域是有界閉凸集。以此為基礎提出了求解該模型的一種全局優化解法——最優值線段算法。最后的實例說明了該模型和全局優化方法的有效性和實用性。

[1] Gerbert B G.Some Notes on V-belt Drives[J].ASME Journal of Mechanical Design,1981,103(1)：8-18.

[2] Shieh C J,Chen W H.Effect of Angular Speed on Behavior of a V-belt Drive System[J].International Journal of Mechanical Sciences,2002,44(9)：1879-1892.

[3] 劉雍德.V帶傳動設計方法探討[J].湖北汽車工業學院學報,1997(3)：1-4.

[4] Sharma CS,Purohit K.Design of Machine Elements[M].New Delhi：Prentice Hall of India,2003.

[5] Hamrock B J,Schmid S R,Jacobson B O.Fundamentals of Machine Elements[M].2nd Edition.New York：McGraw-Hill Science,2004.

[6] Bhandari V B.Design of Machine Elements[M].New Delhi：Tata McGraw Hill Publishing,2007.

[7] 宋俐,魏鋒濤,劉偉.基于改進遺傳算法的帶傳動多目標模糊優化設計[J].機械傳動,2006,30(5)：28-30.

[8] Shim H J,Kim J K.Cause of Failure and Optimization of a V-belt Pulley Considering Fatigue Life Uncertainty in Automotive Applications[J].Engineering Failure Analysis,2009,16(6)：1955-1963.

[9] 龔小平,仝崇樓,劉永強,等.V帶傳動可靠性優化設計[J].現代機械,2002(1)：50-52.

[10] 嚴寒冰,原思聰,季文祥.基于遺傳算法及MATLAB的 V帶傳動優化設計[J].機械,2008,35(9)：23-25.

[11] 劉金石.按工作壽命優先或最大轉矩優先設計V帶傳動[J].四川工業學院學報,1992,11(1)：13-18.

[12] 劉雍德.不同預期壽命時V帶傳動額定功率計算方法的研究-對IS05292-1980計算方法的改進[J].中國機械工程,1996,7(增刊)：90-92.

[13] Spotts M F.Design of Machine Elements[M].6th Edition.Englewood Cliffs：Prentice-Hall Inc.,1985.

[14] 羅善明,余以道,郭迎福,等.帶傳動理論與新型帶傳動[M].北京：國防工業出版社,2006.

[15] 劉明潔,趙洪志,陳福恩.預測V帶壽命的研究[J].農業機械學報,1994(增刊)：123-128.

[16] 劉雍德.V帶的壽命計算[J].湖北汽車工業學院學報,1997(4)：1-4.

[17] 陳立周.機械優化設計方法[M].北京：冶金工業出版社,2005.

[18] 李董輝,童小嬌,萬中.數值最優化算法與理論[M].北京：科學出版社,2010.

[19] 機械設計手冊編委會.機械設計手冊：帶傳動和鏈傳動[M].北京：機械工業出版社,2007.

[20] 楊宗棟,曹助家.普通V帶傳動的預期壽命[J].東北重型機械學院學報,1989,13(4)：56-63.