機床導軌熱誤差優化計算中的近似模型方法

李郝林 應杏娟 遲玉倫

上海理工大學,上海,200093

0 引言

在精密機床的切削加工中,熱源對加工精度的影響極大,提高工件的加工精度必須對機床的熱變形作定量研究,并在加工過程中作合理控制與補償。機床導軌與工作臺的相對運動會產生大量的摩擦熱,造成導軌與工作臺的熱變形,影響刀具與工件之間的相對位置關系,最終影響工件的加工精度。為提高刀具的加工精度,需要獲得導軌整個行程范圍內的熱變形動態變化量,以便進行實時誤差補償。但是,對導軌全行程范圍內進行熱誤差實時測量目前還沒有有效的方法[1-4]。

隨著有限元理論的不斷完善和數值模擬技術的日趨成熟,數值模擬技術在熱特性分析領域得到了廣泛應用,成為熱變形分析的重要手段。有限元數值模擬技術可以定量地計算出溫度分布狀態和由溫度產生的熱位移、應力和應變等數據,這些模擬結果對機床的熱特性分析有一定的指導意義。但由于有限元分析邊界條件的不確定性,故無法給出精確的計算結果,只能給出定性的分析結果。要得到接近實際值的最優計算結果,必須將有限元數值模擬技術與優化技術相結合[5-6]。文獻[7-8]提出了有限元模型的實驗校準方法,將計算結果與實驗結果相比較,從而對有限元模型進行校準。本文提出了采用近似模型優化方法進行機床導軌熱變形有限元模型邊界條件優化選擇的方法。采用試驗設計方法進行數據采樣,為了使數值模擬結果逼近實驗結果,以導軌熱變形計算誤差平方和作為優化目標函數,以有限元分析的邊界條件為設計變量,采用響應面法建立設計變量和目標函數的近似模型,利用導軌測量點位置處熱變形的實際測量數據,修正有限元計算邊界條件,從而得到接近實際測量值的全行程范圍內的導軌熱變形誤差實時動態變化值。

1 響應面近似模型方法簡介

1.1 響應面近似模型

在研究導軌熱變形誤差有限元分析過程中,由于有限元模型的邊界條件很難在理論上精確確定,故使得有限元計算結果與實驗結果之間往往存在明顯的誤差,為了縮小這種誤差,本文借助響應面方法進行有限元模型修正。

響應面法以試驗設計為基礎,用于的處理多變量問題的建模和分析。通過近似構造一個目標函數響應y和一組設計變量x相關的低階多項式,以顯式的響應面近似模型逼近目標函數響應y與設計變量x之間復雜的隱式關系[9-11]。本文使用該方法,根據導軌熱變形的實際測量數據,修正有限元模型的邊界條件(對流傳熱系數和熱源)。

工程中最廣泛采用的響應面近似函數為二階模型[12-13]：

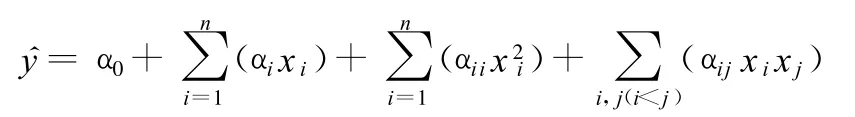
式中,n 為設計變量總數;xi、xj為 設計變量;α0、αi、αii、αij(i＜j)為多項式的待定系數。

將上式轉換成多元線性回歸模型,可得統一的簡單形式：

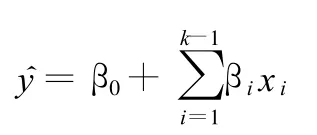
其中,β0、βi為待定系數,k是待定系數βi的個數。為了確定βi,需要做m次的獨立實驗,m≥k,通過求解得到相應的系數βi。對于4個設計變量的情況,待定系數βi的個數k=15,至少進行15次獨立實驗。

設ε為服從正態分布N(0,σ2)的響應面回歸值與實驗值之間的誤差。為了估計二次多項式的系數βi,可以用最小二乘法,使誤差平方和S最小,即

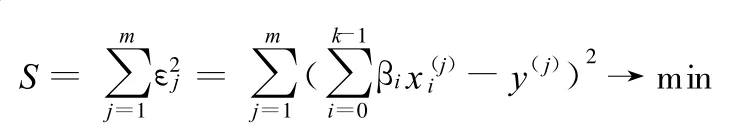
根據變分原理,令

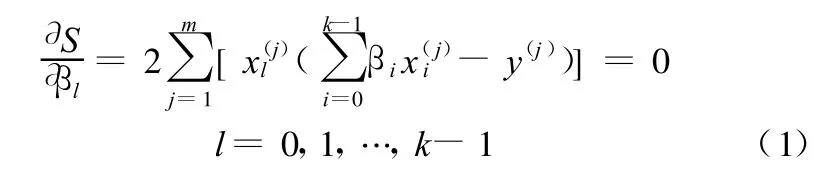
解式(1)即可得到待定系數βi的無偏差估計值。以上是響應面法的基本原理及響應面系數求解的具體方法。

1.2 響應面模型評價指標

1.2.1 復相關系數R2

復相關系數R2描述響應面函數對實驗數據的擬合程度,定義如下：

R2是一個在[0,1]之間變化的值,其值越接近1說明誤差的影響越小,即回歸方程越精確[14]。

1.2.2 響應面函數的顯著性檢驗

通過方差分析和F檢驗確定回歸模型是否可以作為有意義的近似模型。

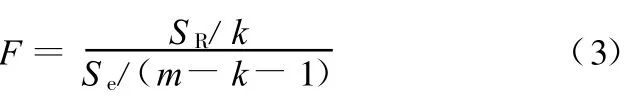
服從F分布[14]。對于給定的顯著水平α,由F分布表查出Fα(k,m-k-1),若F ＞Fα(k,m-k-1)成立,則認為在α水平下該響應面模型有意義。

2 數控機床導軌熱誤差的測量

熱誤差的測量實驗在精密導軌試驗臺上進行,試驗裝置和傳感器安裝方式如圖1所示。考慮工作臺的運動問題,傳感器選用非接觸位移傳感器,選用 HEIDENHAIN公司的capaNCDT6100精密位移傳感器。對于數控主軸磨床類機床,軸向(Z方向)和縱向(Y方向)對工件加工精度影響不大,所以本文考慮分析具有典型意義的橫向(X方向)熱變形誤差沿導軌運動方向的分布,坐標方向見圖1。

圖1 機床導軌熱變形測量試驗裝置

沿導軌運動方向(Z方向)安裝r個位移傳感器(本文以3個傳感器為例說明所提出的計算方法)。其中1個位移傳感器放置在中間位置,其余2個分布在導軌兩端,圖1中C1、C2、C3測點位置即傳感器安裝位置。工作臺運行速度為60m/min,連續運行240min(4h),每隔一定時間讀取位移傳感器的測量值,并根據測量值計算出水平方向的熱變形量誤差。

設傳感器 1、2、3 的讀數分別為 δ1(i)、δ2(i)、δ3(i),i=0,1,…,N(N為測量序號),本例設定每20min測量一次,共測量12次,則N=12。測量開始時主軸熱變形為0,設傳感器1、2、3的讀數分別為 δ1(0)、δ2(0)、δ3(0),則第 i次測量 X 方向 1、2、3傳感器位置處的熱變形量分別為

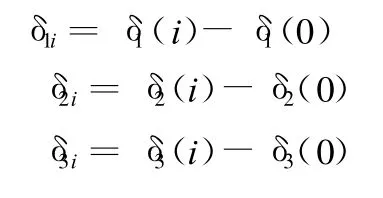
3 機床導軌熱特性分析響應面模型的建立

本文研究的對象(自制精密導軌試驗臺)主要由導軌、滑塊、工作臺、床身等組成,主要熱源是滾珠導軌與滑塊之間以及滾珠絲杠副的摩擦發熱。

建立響應面模型之前,先通過對給定邊界條件(發熱量、對流系數等)導軌熱變形進行有限元數值熱變形分析,獲得導軌全程范圍內的熱變形結果,并與實際實驗結果比較。

計算中使用有限元分析軟件建立并經過簡化的導軌試驗臺有限元模型,如圖2所示。簡化原則為：①忽略對計算結果影響不大的細小結構;②試驗臺床身機架、絲杠等零件不參與建模;③床身底部用螺釘固定,在 X、Y、Z方向沒有熱位移。

溫度場分析采用SOLID87單元,熱變形分析轉換為結構單元SOLID92。計算時假定環境溫度為20℃。

圖2中C1、C2、C3表示與實驗中傳感器位置對應的測點位置。當工作臺進給速度為60m/min時,計算得到前后導軌和滑塊表面的熱流密度分別為1000W/m2和3000W/m2;導軌和床身靜止表面與空氣間的對流換熱系數取10W/(m2?K);當工作臺運動速度為60m/min時,計算得到對流換熱系數為50W/(m2?K)[15]。

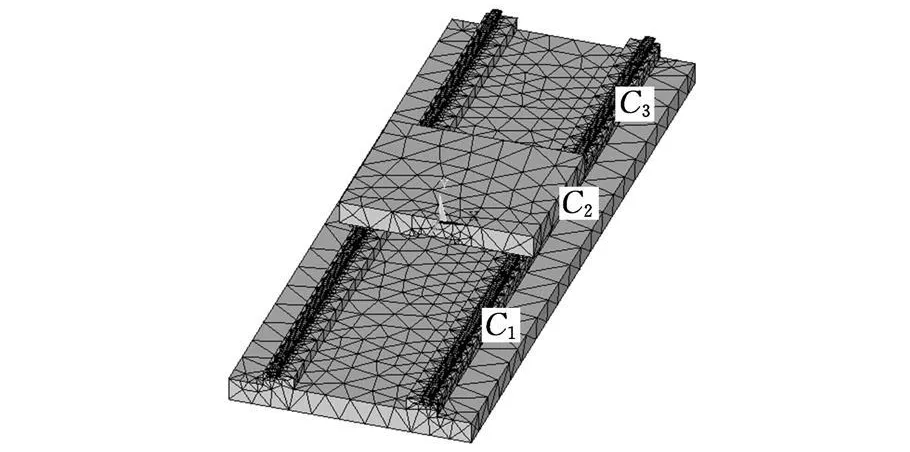
圖2 導軌試驗臺有限元模型

在上述邊界條件下,計算得到導軌運動4h的熱誤差分布如圖3所示。計算值與實驗數據比較,最大誤差為 6.4μm,誤差平方和為813μm2。可以看出,計算值和實驗數據有較大的差別,這是因為有限元模型熱源和邊界條件的不確定性影響了計算精度。為使計算結果逼近實驗結果,需要對影響計算結果的有限元模型的邊界條件進行優化,以便對機床導軌熱誤差進行優化計算。

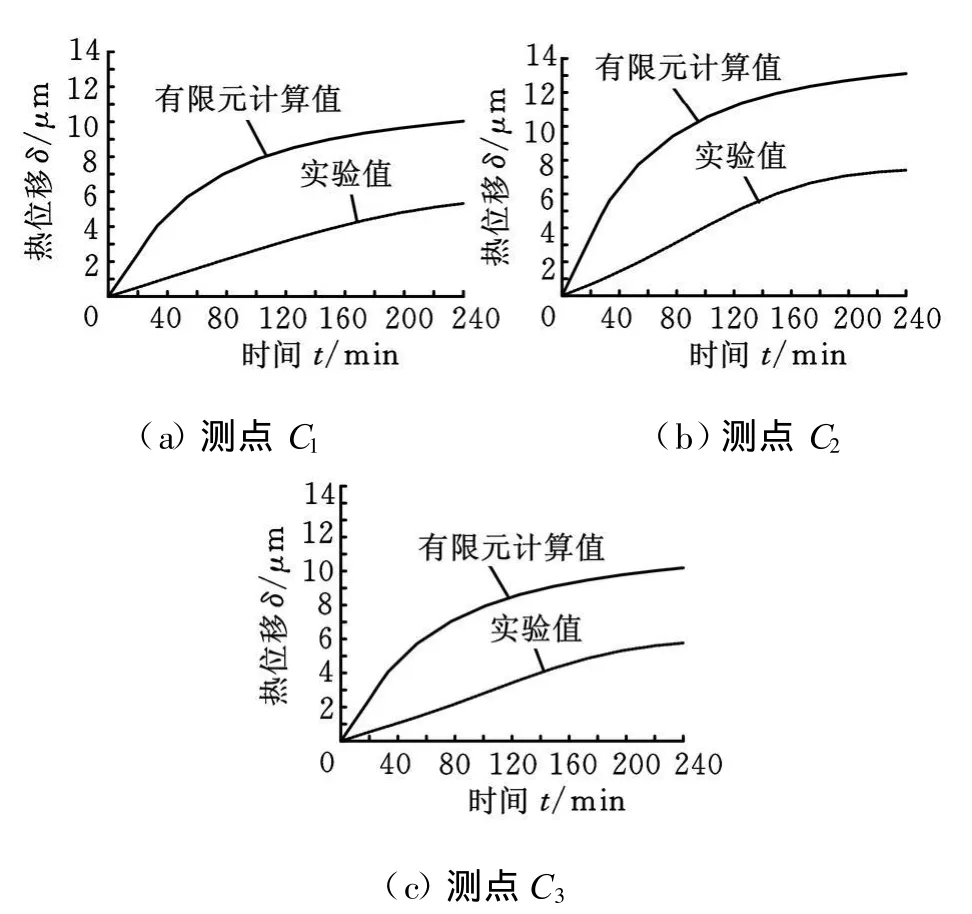
圖3 熱誤差比較曲線(優化前)

本文提出應用近似模型方法進行優化計算,必須首先建立對應的數學模型,包括選取設計變量,設計目標函數,給出約束條件等。

3.1 目標函數

為了使數值模擬結果逼近實驗結果,取導軌上3個傳感器安裝位置的熱變形計算誤差平方和作為目標函數,用F(Ω)表示,作為設計變量Ω的優化計算指標。

對C1、C2、C3測點熱變形誤差模擬計算值Δ1i、Δ2i、Δ3i與實際測量值δ1i、δ2i、δ3i進行比較 ,其

誤差分別為 ω1i= Δ1i-δ1i;ω2i= Δ2i-δ2i;ω3i=Δ3i-δ3i,i為測量序號,i=0,1,…,N 。

我們的優化目標是上述誤差越小越好,所以取其誤差平方和構造設計變量 Ω的優化計算指標

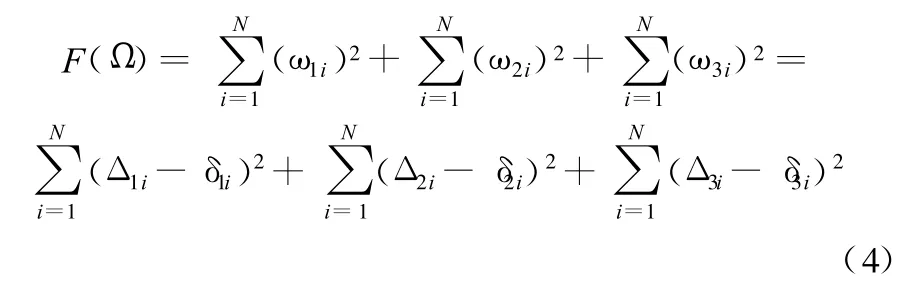
本例中工作臺運動4h,每20min讀取一次熱誤差值,i=12。

3.2 設計變量

在對機床導軌熱變形誤差進行有限元分析的過程中,上述計算的有限元模型的邊界條件(對流傳熱系數和熱源)與實際有較大誤差,很難從理論上精確確定,使得有限元計算結果與實驗結果之間往往存在明顯的誤差。因此本文選擇導軌和滑塊表面對流系數(ξ1、ξ2),導軌和滑塊發熱表面的熱流密度(Q1、Q2)作為設計變量 Ω。

在理論計算的基礎上結合經驗選取設計變量的因子水平范圍,如表1所示。

表1 設計變量因子水平范圍表

為使實驗點分布得比較均勻,將4個設計變量在各自范圍內均勻取5水平。為便于計算研究,將設計變量進行中心編碼[-1,1]轉換,形成新的設計變量

3.3 響應面模型的建立

4因子的二階響應面采用完整二次型,其實驗次數至少需進行(4+1)(4+2)/2=15組[14]。均勻設計方法是利用數論方法在設計空間中均勻分布實驗點集,是一種有效的部分因子實驗方法,特別適合多因素、多水平的試驗設計[16]。所以本文采用4因素16水平的均勻試驗表(采用擬水平法),另外在零點增加一組實驗,對總共17組實驗進行有限元分析。對于每組實驗(有限元計算),計算導軌的X方向變形量,并與采用前述方法獲得的測量值進行比較,計算出優化計算指標F(Ω)值。

采用第1節所述響應面方法公式建立優化計算指標F(Ω)和設計變量 Ω之間的近似模型。得到響應面函數表達式

根據式(2)計算得到復相關系數R2=0.9825,接近1,說明回歸方程足夠精確。

對目標函數的二階響應面模型方程進行F檢驗,根據式(3)計算統計量F,得到F=120.5＞F0.05(14,2)=19.4,說明響應面模型是有意義的。

4 數控機床導軌有限元模型的優化及熱誤差計算

對于數控機床導軌有限元模型,為使數值模擬結果逼近實際測量結果,其優化目標應盡可能減少由于有限元模型邊界條件難于精確確定所導致的有限元計算誤差。

綜上所述,導軌有限元分析模型優化的數學模型為

這樣,有限元模型優化問題就轉化為對上式的求解。

采用上述優化數學模型并選擇優化算法,對導軌有限元模型邊界條件進行優化設計。得到一組 最 優 設 計 變 量

根據優化后的邊界條件,利用有限元分析軟件計算導軌在整個行程范圍內的熱變形量。

優化后的導軌橫向(X方向)熱誤差比較曲線如圖4所示。仍選取C1、C2、C3三個測點,將有限元計算結果與實驗結果進行對比,計算值與實驗結果已非常接近。對照圖3優化前的曲線,其最大誤差(實驗值與計算值之間的誤差)已經由6.4μm 降低為0.83μm,誤差平方和F(Ω)由優化前的 813μm2降低為 11.2μm2。

5 結束語

在研究導軌熱變形誤差有限元分析的過程中,由于有限元模型的邊界條件很難從理論上精確確定,使得有限元計算結果與實驗結果之間往往存在明顯的誤差。響應面方法的優勢在于可以通過較少的實驗(有限元計算)獲得設計變量(有限元模型邊界條件)和目標函數(熱變形計算誤差平方和)之間足夠準確的相互關系,并且可以只用簡單代數表達式展現出來。因此,為了縮小計算誤差,本文借助響應面方法進行有限元模型修正。通過實驗得到3個測點的熱誤差變化值,建立了優化計算指標(3個測點的計算誤差平方和)和設計變量(熱源和對流系數)之間的近似模型,對導軌有限元邊界條件進行了優化選擇,使得計算誤差明顯降低。獲得了導軌整個行程范圍內的接近實際測量值的熱變形動態變化計算值,以便進行實時誤差補償。但本文中的優化選擇是在一個運行條件下以3個測點為例進行的,對于大型機床導軌,為了提高計算精度可以設置3個以上測點進行優化,另外,如何將近似模型應用于復雜運行條件(如運行時開啟關閉機床)需要進一步研究。

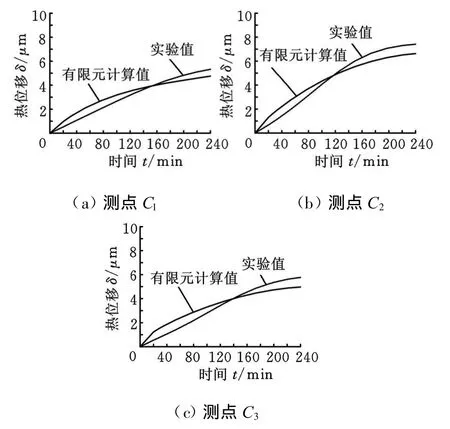
圖4 熱誤差比較曲線(優化后)

[1] Koevoets A H,Eggink H J,van der Sanden J,et al.Optimal Sensor Configuring Techniques for the Compensation of Thermo-elastic Deformations in High-precision Systems[C]//13th International Workshop on Thermal Investigation of ICs and Systems.Budapest,2007：208-213.

[2] Yang JG,Ren Y Q,Liu G L,et al.Testing Variable Selecting and Modeling of Thermal Errors on a INDEX-G200 Turning Center[J].International Journal of Advanced Manufacturing Technology,2005,26：814-818.

[3] 楊建國,任永強,朱衛斌,等.數控機床熱誤差補償模型在線修正方法研究[J].機械工程學報,2003,39(3)：81-84.

[4] 閆嘉鈺,張宏韜,劉國良,等.基于灰色綜合關聯度的數控機床熱誤差測點優化新方法及應用[J].四川大學學報(工程科學版),2008,40(2)：160-164.

[5] Zhao Haitao,Yang Jiangguo,Shen Jinhua.Simulation of Behavior of a CNCMachine Tool Spindle[J].International Journal of Machine Tools and Manufacture,2007,47：1003-1010.

[6] 郭勤濤,張令彌,費慶國.結構動力學有限元模型修正的發展——模型確認[J].力學進展,2006,36(1)：36-42.

[7] Carrion F J,Lozano A,Fabela M J,et al.Simplified Experimental Calibration for a Tridilosa-type Bridge Finite Element Model[J].Experimental Mechanicaics,1999,39(4)：324-328.

[8] Choi J K,Lee D G.Thermal Characteristics of the Spindle Bearing System with a Gear Located on the Bearing Span[J].International Journal of Machine Tools&Manufacture,1998,38(9)：1017-1030.

[9] Romero V J,Swiler L P,Giunta A A.Construction of Response Surface Based on Progressive-latticesampling Experimental Designs with Application to Uncertainty Propagation[J].Structural Safety,2004,26(2)：201-219.

[10] 李郝林,應杏娟.數控機床主軸系統熱誤差溫度測量點的最優化設計方法[J].中國機械工程,2010,21(7)：804-808.

[11] Kim T,Park H,Rhee S.Optimization of Welding Parameters for Resistance Spot Welding of TRIP Steel with Response Surface Methodology[J].International Journal of Production Research.2005,43(21)：4643-4657.

[12] 席光,王志恒,王尚錦.葉輪機械氣動優化設計中的近似模型方法及其應用[J].西安交通大學學報,2007,41(2)：125-135.

[13] 趙祖德,陳學文,陳軍,等.基于近似模型和數值模擬的連桿熱鍛成形工藝設計優化[J].上海交通大學學報,2008,42(5)：748-751.

[14] 張小云.雙相鋼點焊熔核界面撕裂失效機理與控制方法研究[D].上海：上海交通大學,2008.

[15] 王斌.機械設計手冊[M].北京：機械工業出版社,2004.

[16] Montgomery D C.Design and Analysis of Experiments[M].北京：中國統計出版社,1998.