一類新的6維李代數及其相關的Liouville可積哈密頓系統＊

郭福奎,馮濱魯,魏 媛,張玉峰

(1.山東科技大學,山東 青島 266510;2.濰坊學院,山東 濰坊 261061; 3.濱州學院,山東 濱州 256600;4.中國礦業大學,江蘇 徐州 221116)

1 引言

近年來可積系統理論有了迅速的發展,文獻[1-4]中給出了尋求可積系統的方法。其中一種方法是著名的Lax法,它是由屠規彰教授提出的[5],后來稱之為屠格式。在本文中我們將利用屠格式得到新的可積系統。因此,我們簡單的介紹一下屠格式。

設G是數域C上的矩陣李代數。令G=G?C(λ,λ-1)是其相應的loop代數,其中 C(λ,λ-1)表示一組關于參數λ的洛朗多項式。G中基元的階數可定義為deg(x?λn)=n,x∈G。

首先,記靜態零曲率方程

的解為V=V(λ),且Vx(n)=(λnV)++Δn滿足

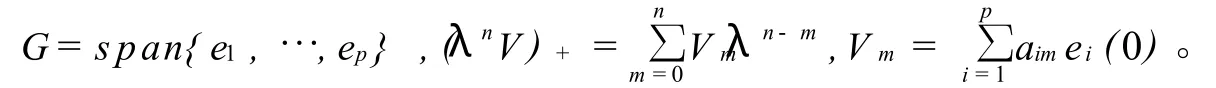
其次,利用零曲率方程

可以得到Lax可積方程族

最后,根據方程(1)我們可以得到哈密頓算子J和循環算子L,因此方程(4)可以寫成哈密頓形式

其中 Hn(n∈Z)表示方程(5)的守恒密度,可以由跡恒等式[5]

計算得到,其中〈A,B〉表示矩陣的跡,例如〈A,B〉=tr(AB),?A,B∈G。由文獻[5]的論述可知,如果JL =L＊J,那么Lax可積方程族(4)是Liouville可積的。

可積系統一個重要的擴展方向是可積耦合,可積耦合是在文獻[6-7]提出的,并作了相關的研究。對可積耦合的研究不僅可以幫助我們探討可積系統的對稱,還可以幫助我們發現不同進化方程的可積方程族之間的關系。例如在文獻[8]中我們構造了一個可積模型(實際上是可積耦合)把著名的A KNS方程族和KN方程族聯合在一起。郭福奎教授和張玉峰教授在文獻[9]中提出一種簡便有效地推導可積耦合的方法,其要求李代數G可以分解成兩個直和子代數G1,G2它們滿足

其中⊕表示直和,[,]表示李括號。……