關(guān)于(g,f)-3-消去圖＊

張?jiān)?/p>

(濰坊學(xué)院,山東 濰坊 261061)

1 引言

本文所考慮的圖均指有限無(wú)向簡(jiǎn)單圖。設(shè)G是一個(gè)圖,分別用V(G)和 E(G)表示圖G的頂點(diǎn)集和邊集,用 dG(x)表示頂點(diǎn) x在G中的度數(shù)。設(shè) g和f是定義在V(G)上的非負(fù)整數(shù)值函數(shù),并且對(duì)于任意的x∈V(G)有g(shù)(x)≤f(x)。圖G的一個(gè)(g,f)-因子是G的一個(gè)支撐子圖F使對(duì)任意的x∈V(G)有g(shù)(x)≤dF(x)≤f(x)。特別地,若圖 G本身是一個(gè)(g,f)-因子,則稱 G是一個(gè)(g,f)-圖。設(shè) a,b是兩個(gè)非負(fù)整數(shù),若對(duì)任意的?x∈V(G)有 g(x)=a,f(x)=b則稱G的一個(gè)(g,f)-因子為[a,b]-因子;類似地,稱一個(gè)(g,f)-圖為[a,b]-圖。若圖 G的任何一條邊e,G都有一個(gè)(g,f)-因子不含e,則稱圖 G是一個(gè)(g,f)-消去圖;類似地,可定義[a,b]-消去圖。

2 預(yù)備引理

引理1 設(shè) G是一個(gè)圖,g和f是定義在V(G)上的兩個(gè)整值函數(shù),且 g＜f,若對(duì)任意的 x,y∈V(G),且 x≠y,有 f(x)dG(y)≥dG(x)g(y),則 G有(g,f)-因子。

引理2 設(shè) G是一個(gè)圖,g和f是定義在V(G)上的兩個(gè)整值函數(shù),且 g＜f,則圖 G是一個(gè)(g,f)-3 -覆蓋圖當(dāng)且僅當(dāng)對(duì)V(G)的所有不交子集S和T有

定義ε(S,T)如下

3 主要定理及其證明

定理 設(shè)G是一個(gè)圖,g和f是定義在V(G)上的兩個(gè)整值函數(shù),且 g＜f-1,若對(duì)任意的 x,y∈V (G),有 f(x)≤dG(x)且 f(x)(dG(y)-3)≥dG(x)g(y),則 G是(g,f)-3-消去圖。

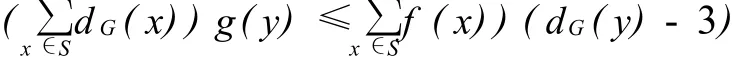
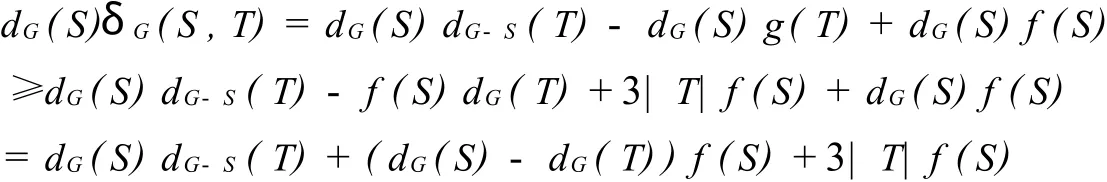
注意到 dG(S)-dG(T)≥-dG-S(T),所以

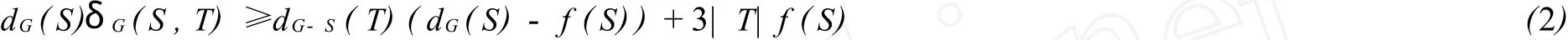
情形1 若G[T]中至少有3條邊,這時(shí)必有|T|≥3,且

將(4)代入(2)式得

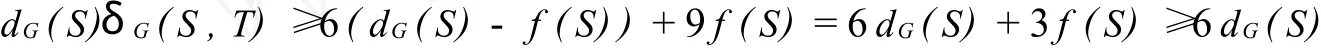
因?yàn)?dG(x)≥g(x),所以 dG(S)≥f(S)≥3|S|≥3

所以 δG(S,T)≥6

情形2 若 G[T]中只有2條邊,且eG(T,V(G)(S∪T))≥1此時(shí)必有|T|≥3且

將(4)代入(2)式得

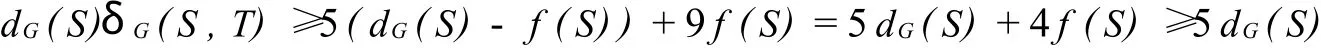
所以 δG(S,T)≥5

此時(shí)|T|≥2且

dG(T)≥eG(S,T)+4=dG(T)-dG-S(T)+4 即

將(5)代入(2)式得

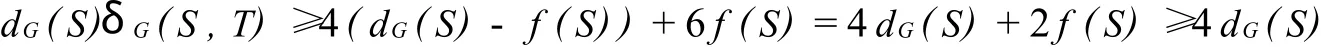
所以 δG(S,T)≥4

情形4 若上述3種情況都不滿足,且 G[T]中只有1條邊,且eG(T,V(G)(S∪T))=1;或 G[T]中沒(méi)有邊,且eG(T,V(G)(S∪T))≥3

此時(shí)|T|≥2且 dG(T)≥eG(S,T)+3=dG(T)-dG-S(T)+3 即

將(6)代入(2)式得

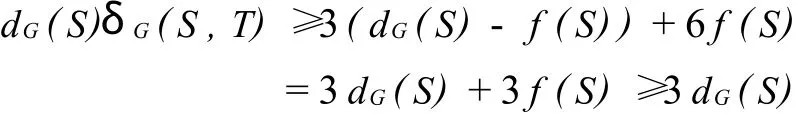
所以 δG(S,T)≥3

情形5 若上述4種情況都不滿足,且 G[T]中只有1條邊,且eG(T,V(G)(S∪T))=0;或G[T]中沒(méi)有邊,且eG(T,V(G)(S∪T))=2

此時(shí)|T|≥2且

將(7)代入(2)式得

所以 δG(S,T)≥2

情形6 若上述5種情況都不滿足,且 G[T]中沒(méi)有邊,且eG(T,V(G)(S∪T))=1;此時(shí)|T|≥1且

將(8)代入(2)式得

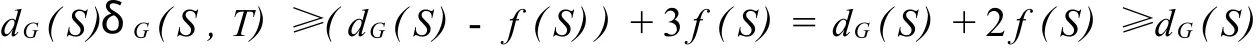
所以 δG(S,T)≥1

情形7 若上述6種情形都不成立。此時(shí)dG-S(T)≥0,又dG(s)≥f(S),于是δG(S,T)≥0。這樣在S≠Φ時(shí)證明了δG(S,T)≥ε(S,T)成立。

當(dāng) S=Φ時(shí),有δG(S,T)=dG(T)-g(T)≥3|T|≥ε(S,T)