層合薄壁圓柱殼1∶1內共振研究

王延慶，梁 力，郭星輝，樓玲娜

(1.東北大學 應用力學研究所，沈陽 110004;2.東北大學 資源與土木工程學院，沈陽 110004)

薄壁圓柱殼被廣泛應用于導彈、無人飛機、衛星外殼以及發動機等許多工程機械中。長期以來，學者們對于圓柱殼非線性振動的研究大多局限在模態相隔較遠的情況［1-5］，對于模態相隔較近的情況研究則不多。如果模態相距很近，那么相鄰模態之間會產生耦合作用，對圓柱殼非線性振動的分析影響很大，這給此類問題的研究帶來了一定的困難。在多自由度非線性系統中，當某些線性固有頻率存在近似可通約關系時，振動系統的各階模態強烈地耦合，能量不斷交換，產生內共振。這將對工程中時常發生的超諧波與亞諧波共振產生重要影響，因此對內共振的研究有著重要的意義。白鴻柏［6］對密集模態間的非線性耦合作用做了初步研究，重點考察了密集模態組的整體表現。Thomas［7］利用擾動法分析了簡諧激振下薄壁球殼的1∶1∶2內共振。Abe［8］采用打靶法，研究了夾支薄壁殼在兩個反對稱模態之間產生的1∶1內共振。在國內外的文獻中，對于圓柱殼鄰近模態內共振問題的研究還很少，此類問題仍需要更多的討論與分析。

本文以電機升高片的層合圓柱外殼為研究模型，根據Donnell’s非線性簡化殼理論，建立了系統的非線性振動方程，采用Galerkin方法對振動方程進行離散化。然后應用平均法，求解了系統包含兩個相鄰軸向模態的非線性振動響應，得到了反映復雜內共振的幅頻特性曲線，表明系統存在1∶1內共振現象。最后與數值模擬進行了比較，并且得到了不同參數對層合薄壁圓柱殼復雜振動響應的影響。

1 振動方程

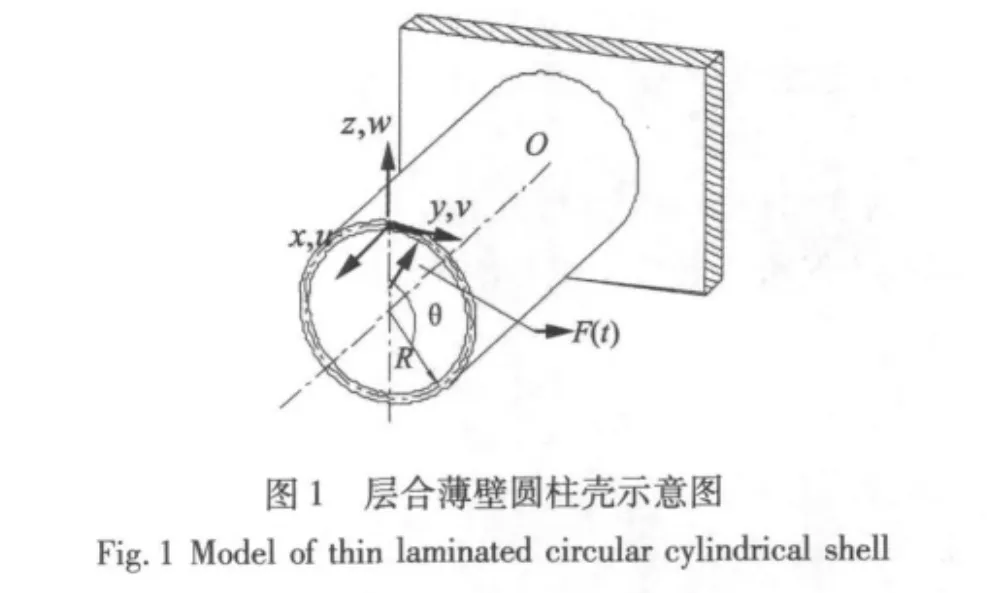
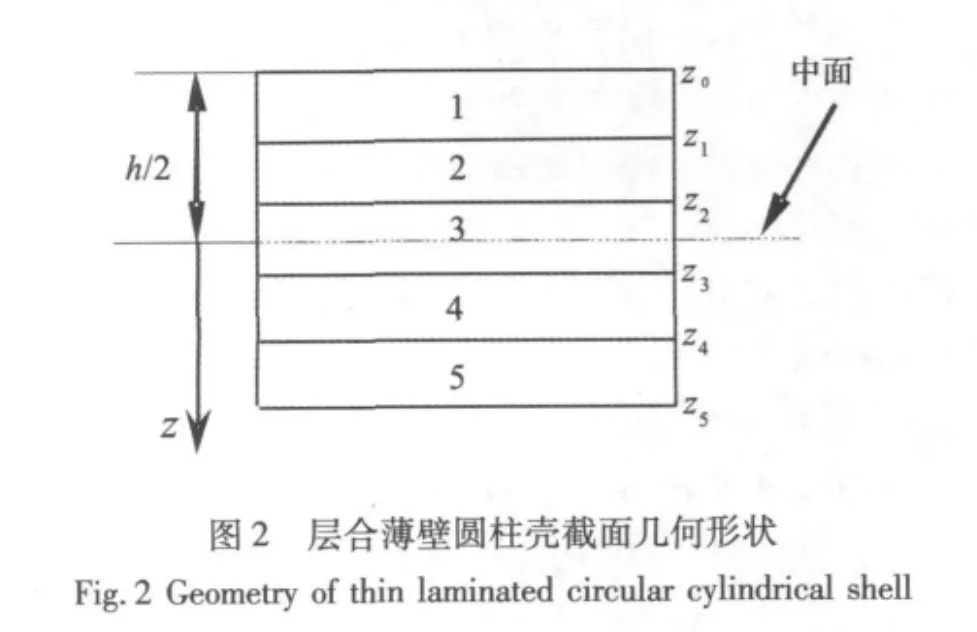
考慮一端固定，一端自由的層合薄壁圓柱殼模型(如圖1)，鋪層材料為玻璃纖維布，它由玻璃纖維正交均勻交織而成，各單層的鋪設角均為0°，截面幾何形狀如圖2所示。

各向同性層合殼第k層的物理方程［9］:

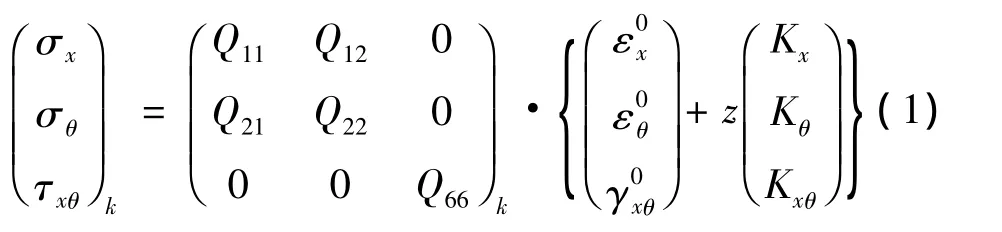
其中Kx，Kθ為中面彎曲撓曲率，Kxθ為中面扭曲率，Qij為折減剛度矩陣，元素表達式為:

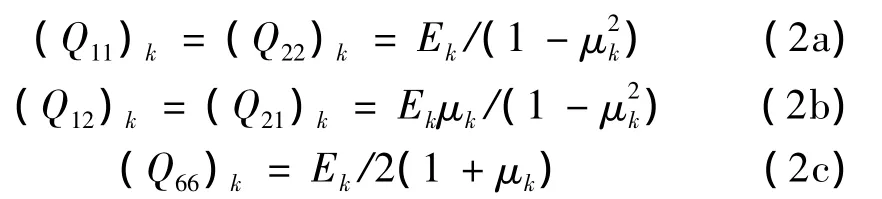
其中:Ek為第k層的彈性模量，μk為第k層的泊松比。

考慮層合圓柱殼的彈性模量隨激振力頻率變化而變化，兩者有如下關系［10］:

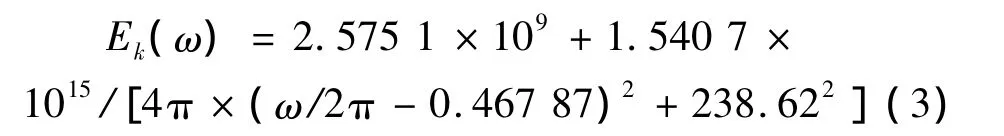
層合殼內力表達式為［9］:

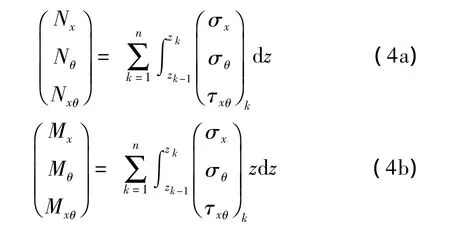
在幾何方程中考慮非線性因素，利用薄殼理論及Donnell’s非線性簡化殼理論得到層合薄壁圓柱殼非線性振動方程［11，12］:

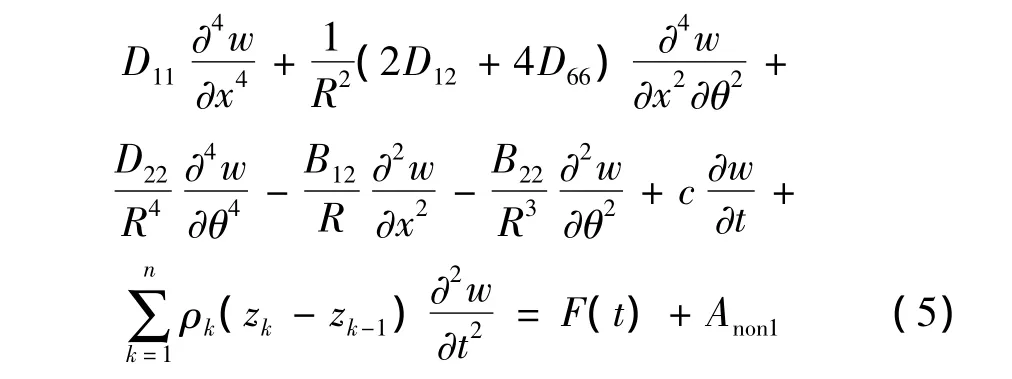
具體表達式見附錄(A1);c為阻尼系數;F(t)為外激振力，作用位置x0=0.34 m，θ0=π/24 rad，表達式為:

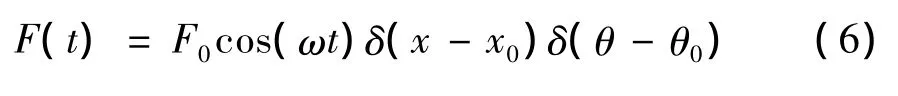
2 平均法過程

本文采用平均法來求解非線性振動方程。由文獻［2］可知，周向模態N對圓柱殼非線性振動特性的影響很小，而軸向模態M影響相對較大，并且考慮到Donnell’s理論對N≥5較為精確，因此本文選擇雙模態(M=1，2;N=6)來分析圓柱殼的非線性動力學行為。位移形式如下:

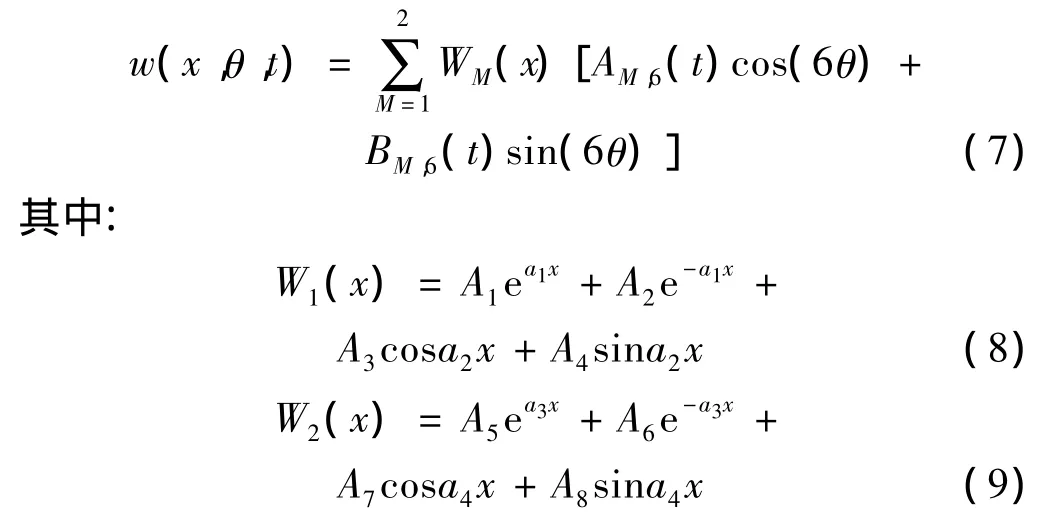
利用Galerkin法對振動方程(5)離散化，得到關于A1，6，B1，6，A2，6，B2，6的 4 個二階非線性常微分方程 (見附錄中A2)。

令:

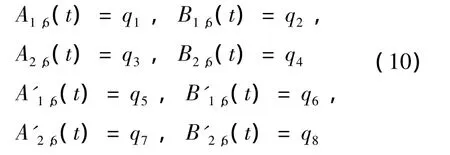
則模態方程組(A2)可以用矩陣形式表示為:

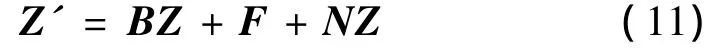
其中Z=［q1q2q3q4q5q6q7q8］T，B，F，N由模態方程組(A2)變形得到。

現構造矩陣:

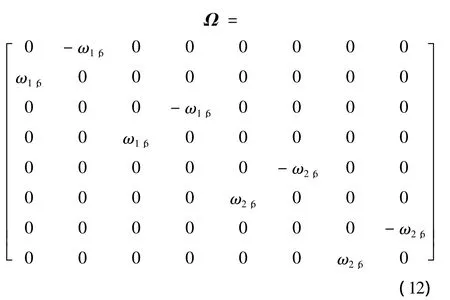
則矩陣 Ω 與矩陣B具有相同的特征值 ± ω1，6i，± ω2，6i，設U為B的特征值所對應的特征向量組成的矩陣，V為矩陣Ω的特征值對應的特征向量組成的矩陣，則有下式成立:

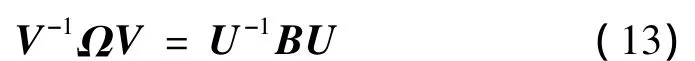
設矩陣P=UV-1，則從方程(13)得到:

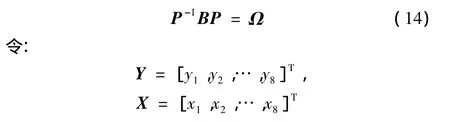
Z=Y，Y=PX，τ=ωt，并在式(11)等號兩端前乘P-1，得到微分方程的標準形:

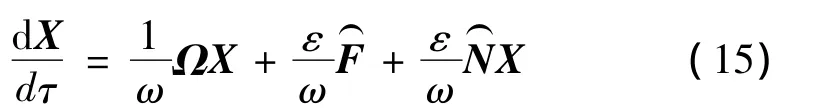
其中ε為小參數。

設激振力頻率ω在某一固定頻率ω0附近變化(這里 ω0= ω1，6)，即:

式中σ是協調參數，表示外激勵頻率ω與ω0的接近程度。

將式(16)代入式(15)，把1/(1+εσ)項展開成冪級數后，保留小參數ε的一次項，得:

引入振幅和相角ai，φi(i=1，…，4):

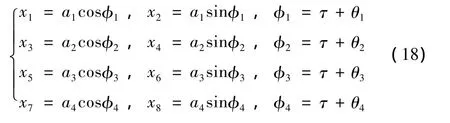
將式(18)中的xi(i=1，2，…，8)對 τ求導并代入式(17)，然后對其應用平均法原理，則可以得到平均方程。為求平均方程定常解，令所有一階導數項等于零，可以得幅頻方程如下:

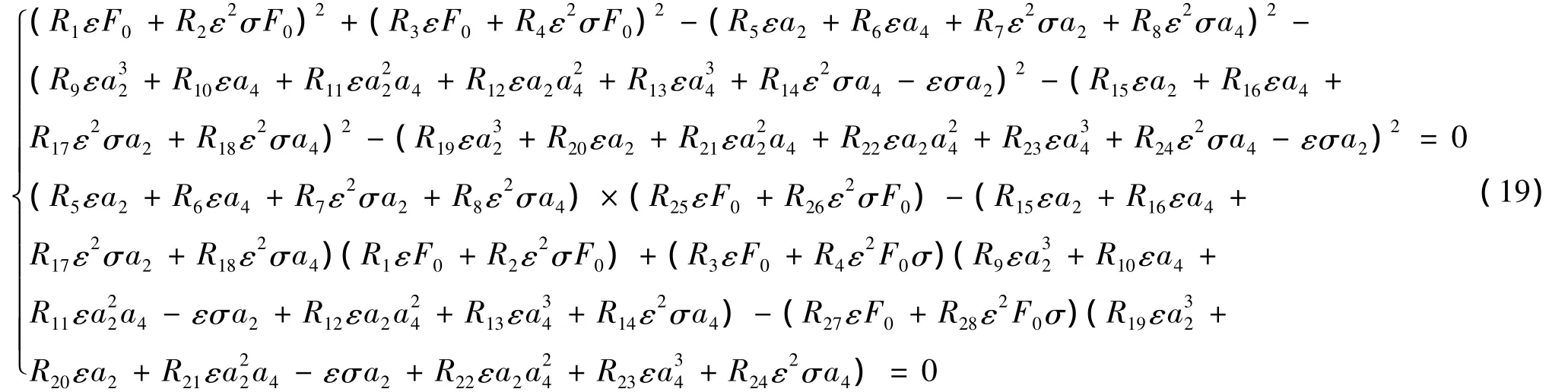
其中Ri(i=1，2，…，28)為平均化產生的積分系數。

3 近似解析解

圓柱殼的幾何及材料參數如下:長度L=0.34 m，中面半徑R=0.090 75 m，層數n=5，單層厚hk=0.000 1 m，泊松比 μk=0.3，殼體密度 ρk=1 951 kg/m3，兩階固有頻率 ω1，6=174.27 × 2π rad/s，ω2，6=179.52×2π rad/s。可以發現兩階固有頻率非常接近，因此系統可能存在1:1內共振。根據方程(19)得到穩態解的幅頻特性曲線，采用李雅普諾夫一次近似理論判斷穩態解的穩定性，結果如圖3所示。其中實線表示穩定的周期解，虛線表示不穩定的周期解。

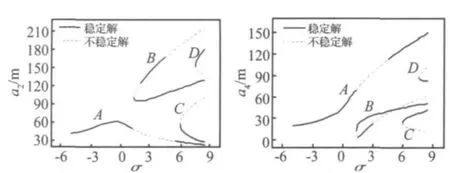
圖3 幅頻特性曲線 (F0=10 N，c=24.7 Nsm-3)Fig.3 Frequency-response curves for F0=10 N，c=24.7 Nsm-3

圖4 時間響應(F0=10 N，c=24.7 Nsm-3，ω =177.8 ×2π rad/s)Fig.4 Response curves for F0=10 N，c=24.7 Nsm-3，ω =177.8 ×2π rad/s

本文考慮外激振力在第一階固有頻率附近。從圖3中看出，不僅系統的第一階模態被激勵起來，第二階模態也同樣被激勵，幅頻特性曲線出現多個解支，并且表現出硬特性。當通過σ=0時，兩階模態表現出不同的變化趨勢，其中第一階模態解支A對應的幅值開始變小，而第二階模態解支A對應的幅值則相反，會繼續增大。當σ增加到1.34時，開始出現多值性，出現解支B，B的兩條分支都隨著σ的增大而增大，并且在σ=1.34～5區間內第二階模態出現了封閉的環解。之后隨著σ的增加，兩階模態都陸續出現兩個分支C和D，當第一階模態處于上半支時，第二階模態跳躍到下半支，它們的變化趨勢相反。圖3中幅頻曲線的變化特點說明，在第一階固有頻率附近，由于兩階模態頻率十分接近，它們之間存在強烈的耦合，兩階模態彼此影響牽制，能量在它們之間傳遞，產生了1∶1內共振。而立方非線性帶有內共振的系統，能量可以很容易地從高階模態傳輸到低階模態，反之則不然［13］，因此第一階模態響應大于第二階模態響應。

從圖4的時間響應中可以更直觀地看出兩階模態間的能量交換，在恒定的激勵作用下，模態響應值不確定，可以在不同解支之間跳躍，當第一階模態的響應較大時，第二階模態的響應較小，反之亦然。

圖5給出近似解析解與數值解的比較，其中數值解采用4階Runge-Kutta方法得到。從圖中可以看出，二者變化趨勢及拐點的位置都相同，只是幅值上有一些偏差。這主要是由于復合材料動態彈性模量隨激振力頻率而變化［10］，數值解中考慮了這種變化，而在解析法中無法考慮這種關系，僅取激勵頻率等于第一階固有頻率時的彈性模量來近似，所以造成了一些誤差。但這不影響我們對系統動力學行為的定性分析。

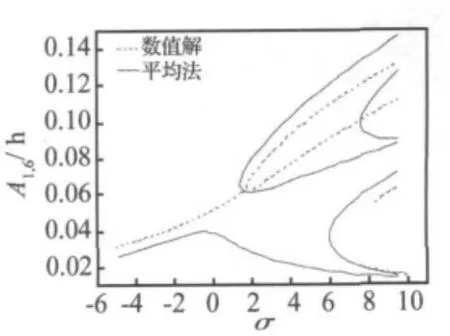
圖5 平均法與數值法比較(F0=10 N，c=24.7 Nsm-3)Fig.5 Frequency-response curves got by averaging method and Runge-Kutta method(F0=10 N，c=24.7 Nsm-3)

圖6 不同激勵幅值下的幅頻特性曲線(c=24.7 Nsm-3)Fig.6 Frequency-response curves of different excitation amplitude for c=24.7 Nsm-3

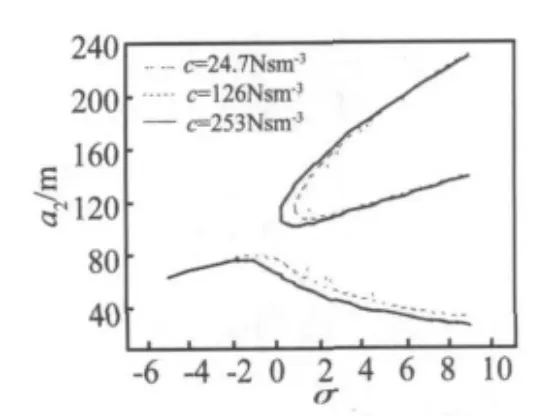
圖7 不同阻尼系數下的幅頻特性曲線(F0=20 N)Fig.7 Frequency-response curves of different damping coefficient for F0=20 N

4 不同參數的影響

本文以第一階模態為例給出不同參數對系統復雜振動響應的影響。圖6給出了不同激勵幅值下系統的幅頻特性曲線。從圖中可以看出，隨著激勵幅值的增大，幅頻曲線的解支有所減少 (如F0=10 N對應的幅頻曲線比F0=5 N對應的幅頻曲線少了一個半橢圓形的解支)，但是系統的硬特性增強。

圖7為不同阻尼系數下的幅頻特性曲線，可以看出阻尼對響應的影響比激勵的影響小得多，振動響應對阻尼不敏感，這主要是由復合材料自身的特性所決定的。

5 結論

本文根據Donnell’s非線性簡化殼理論建立了一端固定，一端自由的層合薄壁圓柱殼的動力學方程，應用平均法求解了系統包含兩個相鄰軸向模態的非線性振動響應，得到以下結論:

(1)由于所選的兩階模態頻率相距比較近，它們之間存在強烈的耦合，彼此影響牽制，能量在兩階模態之間相互傳遞，因此幅頻特性曲線反應出系統內部存在1∶1內共振。

(2)由同種材料鋪設而成的圓柱殼的幅頻曲線表現出硬特性。隨著激振力幅值的增大，系統的硬特性變得更明顯，同時幅頻曲線的解支有所減少;阻尼對振動響應的影響很小，說明玻璃纖維布層合圓柱殼的響應對阻尼不敏感。

［1］Wouters C R.Large amplitude free vibrations of shallow spherical shell and cylindrical shell［J］.International Journal of Nonlinear Mechanics，1985，20(2):69-78.

［2］王延慶，郭星輝，常海紅，等.旋轉薄壁圓柱殼振型進動的非線性振動特性［J］.固體力學學報，2009，30(3):267-279.

［3］Huang K H，Dasgupta A.A layer-wise analysis for freevibration of thick composite cylindrical-shells［J］.Journal of Sound and Vibration，1995，186(2):207-222.

［4］Ganapathi M，Kvaradan T.Nonlinear free flexural vibrations of laminated circular cylindrical shells［J］.Composite Structures，1995，30(1):33-49.

［5］Amabili M， PellicanoF， PaidoussisM P. Non-linear dynamics and stability of circular cylindrical shells containing flowing fluid.Part III:Truncation effect without flow and experiments［J］.Journal of Sound and Vibration，2000，237(4):617-640.

［6］白鴻柏，張培林，陳振藩.密集模態組間非線性相互作用的初步研究［J］.航空學報，2000，21(5):458-461.

［7］Oliver T，Touze C，Chaigne A.Non-linear vibration of freeedge thin spherical shells:modal interaction rules and 1∶1∶2 internal resonance［J］.International Journal of Solids and Structures，2005，42(11-12):3339-3373.

［8］Abe A，Kobayashi Y，Yamada G. Nonlinear dynamic behaviors of clamped laminated shallow shells with one-to-one internal resonance［J］.Journal of Sound and Vibration，2007，304:957-968.

［9］沈觀林，胡更開.復合材料力學［M］.北京:清華大學出版社，2007.

［10］李 健，郭星輝，郭明濤，等.復合材料薄壁圓柱殼動態彈性模量的研究［J］.東北大學學報(自然科學版)，2008，29(12):1770-1773.

［11］ Soedel W.Vibrations of Shells and Plates［M］.New York:Marcel Dekker;1981.

［12］ Wang Y Q，Guo X H，Li Y G，et al.Nonlinear traveling wave vibration of a circular cylindrical shell subjected to a moving concentrated harmonic force［J］.Journal of Sound and Vibration，2010，329(3):338-352

［13］周紀卿，朱因遠.非線性振動［M］.西安:西安交通大學出版社，1998.

附錄:

非線性項:

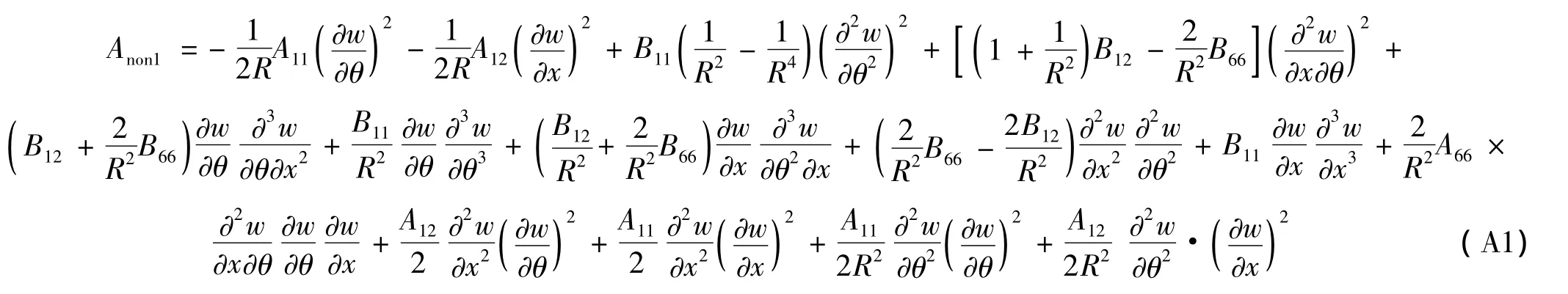
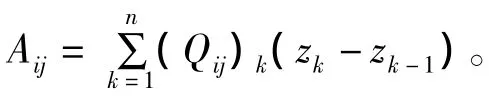
模態方程組:

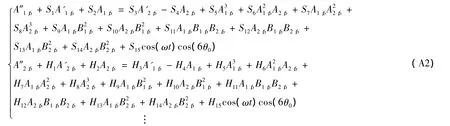
其中:A1，6，B1，6，A2，6，B2，6為時間t的函數，Si，Hi(i=1，2，…，15)為積分系數。