一種地磁導航中的低頻電磁干擾場分離方法

寇義民，夏紅偉，劉 睿，王常虹

(哈爾濱工業大學空間控制與慣性技術研究中心，150080哈爾濱，kouyimin@126.com)

地磁場的精確測量是實現地磁導航的先決條件.由于地磁場的微弱性，提高測量傳感器的靈敏度，以及克服來源于載體自身的磁場干擾是決定測量精度的兩大核心因素.隨著科學技術的快速發展，超高靈敏度的新型磁場測量設備的相繼問世，及傳統的磁測儀器測量精度的不斷提高［1］，使得磁場傳感器的靈敏度已經不再是阻礙地磁場測量精度提高的主要瓶頸，因此，如何克服來源于載體自身的磁場干擾將是提高地磁場測量精度的關鍵.

載體自身的干擾磁場按照其特性可以分為兩類:第一類是與載體運動姿態無關的干擾場，這類干擾除了載體的部件材料被磁化而產生的恒磁干擾之外，通常來自機載的各種電器設備，如無線電設備、電源及輸電線路、電機、數字開關電路等;第二類是與載體運動姿態相關的磁場干擾，包括載體中的軟磁材料被地磁場磁化而產生的激磁干擾，載體在地磁場中運動而產生的渦流磁場干擾等.其中，第二類干擾可以由航磁補償技術解決，即通過求解TOLLES-LAWSON方程來獲取與姿態有關的各類干擾磁場的相關比例系數，進而根據當前載體姿態對干擾場進行估計［2-3］.目前航磁補償技術已經非常成熟，并出現了許多系列化產品，例如加拿大RMS公司生產的AADC-Ⅱ型航空磁自動數字補償儀，可將第二類干擾的影響降低至0.035～0.08 nT(補償后標差)［4］.而對于第一類干擾，目前所能采取的技術手段主要有兩種，即磁屏蔽技術和帶通濾波器技術.然而，前者雖可大幅削弱干擾場強，卻難以完全消除其影響［5］;而后者對于頻率范圍與地磁場相近的干擾磁場則無能為力.如何進一步清除傳統技術手段層層過濾下的“漏網之魚”，也就是強度和頻率都與地磁場信號相近的低頻、弱磁干擾磁場，將是本文研究的重點.

獨立特征量分析法(Independent Component Analysis，簡稱ICA)可有效的對線性疊加的獨立信號進行波形分離［6-11］，并被廣泛應用到了圖像與聲音等信號的處理當中.但由于磁場為矢量場，干擾場的幅值與方向都具有時變特性，它們的疊加并非簡單的線性疊加，故不能將線性ICA方法直接應用于磁場測量信號的分離.針對這個問題，本文提出了全新的解決方案.該方案首先對產生干擾磁場的電路的各個支路各自產生的磁場特性進行了分析，進而將各個支路進行分組，每組支路各自看做是1個獨立干擾源，從而使得每個干擾源都產生相對載體方向固定的干擾場，解決了干擾場方向時變的問題.同時，對載體的姿態提出要求，最終以增加干擾源數目為代價，將各種磁場的疊加由總幅值的非線性疊加，化簡成為在傳感器敏感軸方向上的線性疊加，從而滿足了線性ICA的應用前提.最后，提出使用相關系數的絕對值對分離后的信號波形與地磁圖進行匹配的方法，從而有效克服了ICA自身的模糊性缺陷.

1 ICA方法在磁場信號分離中遇到的困難

1.1 ICA方法簡介

已知有若干個相互獨立的信號源，彼此發出互不相關的波形信號.采用幾個獨立探測器來檢測信號輸出，由于探測器放置位置距離的不同，每個探測器所檢測到的信號波形都是原始n個信號以不同組分比例的線性疊加.檢測信號與源信號有如下關系:

式中觀測向量x代表各傳感器上的信號輸出，向量s代表信號源輸出，定常矩陣A代表兩者之間的線性轉換關系，可稱為混疊矩陣.在工程實踐中，通常只能通過傳感器輸出獲得觀測量x，而無法直接獲得信號源輸出s與混疊矩陣A.ICA方法將利用信號源之間相互獨立的特性和概率統計學的理論，來分離出各個信號源的輸出波形.

由概率論中的中心極限定理可知，多個非高斯獨立隨機信號的線性疊加將比其中任意一路信號更趨近于高斯分布.根據這一理論，尋找合適的線性變換對觀測向量x進行處理，使得結果向量z中各個元素對應的信號所具有的非高斯性都達到最大時，每個分離出來的信號也就最接近原始的單個信號.

實際操作中，ICA的求解過程通常包含以下3個步驟:1)對混合信號的預處理，包括中心化，白化.2)選擇或定義非高斯性(獨立性)的度量，建立目標函數.3)利用某種最優化方法來令目標函數達到極值，從而推導出一種學習方法.常用的代價函數有峰度、微熵、負熵、互信息等.

傳統線性ICA方法中，為確保各個信號源的輸出可被有效分離，通常有以下假設約束必須被滿足:1)各個信號源的輸出必須彼此相互獨立，這是ICA能夠實現的最基本要求.2)最多只能有1個信號源的輸出為高斯分布，多個高斯信號的混疊無法被分離.3)通常要求傳感器的數目等于信號源的數目，也就是令A為滿秩方陣.

除以上約束外，ICA方法還具有如下含混性:

1)ICA只能分析出各個信號源的輸出波形，而無法分析出其對應幅值.這是因為，針對在僅僅已知測量值的情況下，對原始信號輸出幅值乘入1個因子的同時，對系數矩陣相應的列元素除以這個因子，測量結果不變，即換句話說，si/ki可能取代si作為分離后的信號波形結果.

2)分離出的波形結果是亂序的，也就是無法與原始信號源在順序上一一對應.這是因為在僅僅已知x的情況下，可以在式(1)中插入任意的置換陣及其逆矩陣，也就是x=AP-1Ps.這里P為單位陣交換了兩行后的矩陣，如果最終將AP-1作為解得的線性轉換關系，同時將Ps作為分離后的波形結果，那么將產生亂序的情況.

ICA的具體實現算法很多，有信息最大化法，基于極大似然估計的ICA方法，負熵最大化法，EASI算法，快速固定點算法(FPICA)等，具體請參閱文獻［6］，在此不再贅述.

1.2 ICA在地磁導航信號處理中的問題

ICA方法在磁場信號分離與地磁導航中的主要困難有以下2個方面:

1)線性化疊加約束難以滿足，而非線性ICA又難以應用.

為了簡化研究問題，這里假定載體內只存在唯一低頻干擾源，其在載體內各點產生的干擾磁場的強度和方向與相對位置有關.為了將干擾信號與地磁場信號分離，根據ICA的原理，需采用2個分開布置的傳感器.由畢奧 -薩伐爾定律，干擾源在2個傳感器所處位置上的干擾磁場可分別記為k1δH和k2δH(k1和k2是和距離平方成反比的系數，而δH與干擾源的電流強度成正比)，而地磁場在載體內部處處相同，記為H.兩個位置上干擾磁場與地磁場的夾角分別記為θ1和θ2.則由矢量疊加原理和余弦定理，2個傳感器所測得的總磁場強度分別為

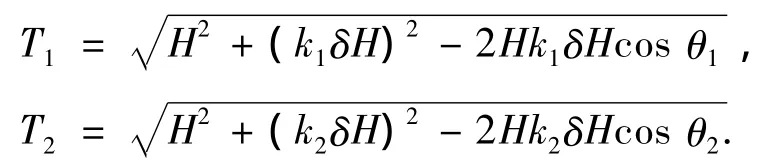
顯然干擾場信號與地磁場信號在傳感器上的疊加屬于非線性疊加，不可能寫成方程(1)的形式，故線性ICA方法難以被直接應用.那么是否可以應用非線性ICA來解決呢?答案是依然很困難.這是因為測量值作為非線性函數時，其參數不僅包含H與δH，還包含角度值θ1和θ2.而這2個角度值也可能是時變的，且互相沒有明顯關聯，只能各自看成獨立信號.這樣傳感器的數目將小于信號源的數目，從而引發新的問題.

2)ICA的含混性對地磁場信號的精確匹配產生障礙.這主要包括以下兩點:1)分離后的信號波形中哪個是地磁場信號波形，哪個是雜波干擾的波形;2)即使正確建立了波形信號間的對應關系，由于幅值不確定性，在其幅值發生變化的基礎上，如何與原始地磁圖進行匹配.

2 解決方案的論證與推導

2.1 各場源信號的線性化疊加模型的建立

為了避免求取總磁場的幅值，引入傳感器敏感軸的概念，一旦敏感軸方向確定，磁場測量值為各磁場信號向敏感軸投影后的疊加值.若兩傳感器的敏感軸與地磁場方向和干擾場方向的夾角分別為α1(t)和β1(t)，α2(t)和β2(t)，則有

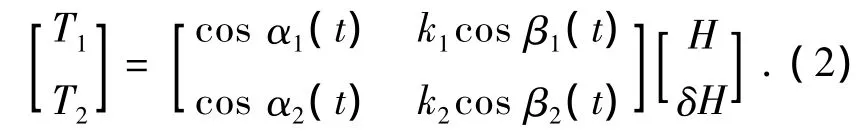
此時地磁場信號與干擾場的信號滿足了線性化疊加，但是系數陣看上去卻是時變的.根據ICA的前提條件，各個獨立信號在傳感器上的輸出比例組分須是固定的，即比例系數M1= cos α1(t)/cosα2(t)和 M2= k1cos β1(t)/ k2cos β2(t)須為時不變的固定值.這里假定β1(t)=β2(t)+γ(t)，代入三角函數有

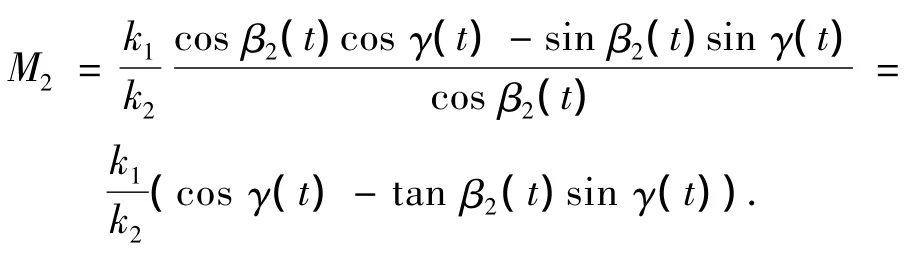
顯然除非保證β2(t)和γ(t)都為時不變的值，否則很難保證M2為固定值，這就要求干擾磁場的方向在各個傳感器的位置處是確定的.M1也與此類似，即只有地磁場方向在載體坐標系內保持不變才能保證M1具有非時變特性.

下面研究干擾磁場矢量相對于載體的方向問題.首先來考慮最簡單的串聯電路.根據畢奧-薩伐爾定律，在t時刻，微小電流源在空間中任意一固定點P產生的磁場矢量為

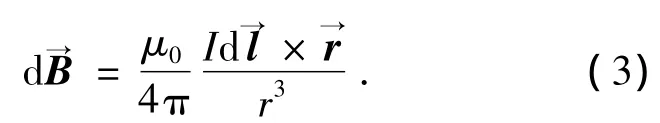
其中，μ0為真空磁導率為由電流源到P點處的矢徑，I為電流強度為導線微元所對應的矢量，進一步展開，可得磁場的幅值為

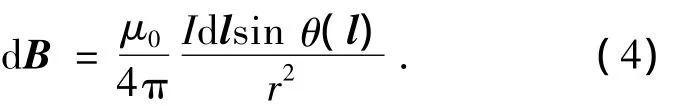
式中θ(l)為在l處導線微元dl與r的夾角，dB的方向由右手定則確定.取串聯電路上的任意n個點處的電流微元，它們在P點處所形成的總磁場為

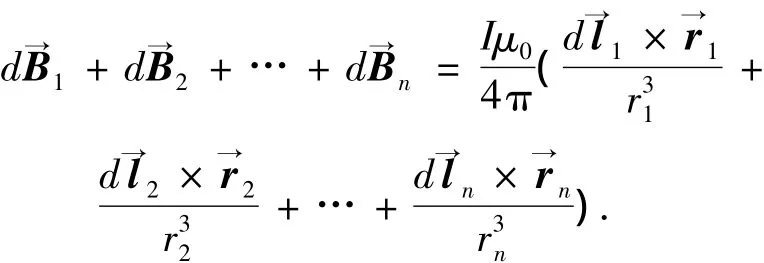
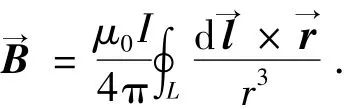
顯然也是1個具有上述性質的矢量.

對于更復雜的含有n個支路的電路(并聯或網狀)，在只含有1個電源的情況下，利用式(3)分別求取t時刻所有n個支路在P點處的總磁場，進行疊加有

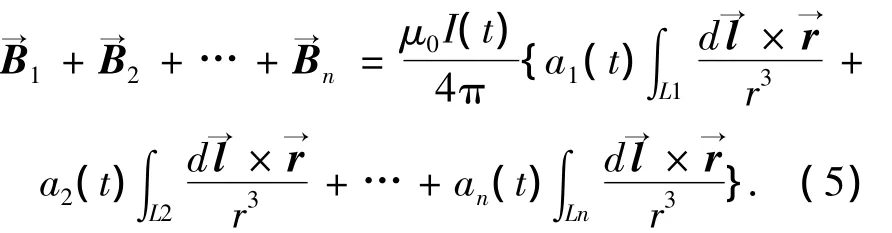
這里I(t)為電源輸出總電流，ai(t)(i=1，2，…，n)表示各支路電流與總電流的比值.此時可分為如下幾種情況分別討論:

1)當各支路不含電感與電抗元件時，ai(t)為非時變固定值，由各支路電阻決定.根據前面證明，大括號中的各個積分項為幅值和方向固定的矢量，它們以固定系數ai(t)所進行的線性疊加仍是幅值和方向固定的矢量，僅和點P的空間相對位置有關.而括號外的系數僅與總電流強度有關.故此時電路產生的干擾磁場與串聯電路產生的干擾磁場具有類似的性質，即方向的確定性.

2)當支路中含有電感或者電抗元件，且I(t)為頻率較高的時變值時，式(5)中的ai(t)也將為時變值，此時該電路產生的總干擾磁場將不具備方向確定性.但由于各個支路各自產生的干擾場仍具備方向確定性，故每個支路可各自作為1個獨立的且具備方向確定性的干擾源來處理.還可將彼此電流強度比值始終恒定的支路分成一組，作為1個干擾源，比如幾個完全對稱的并聯支路.

3)當支路中含有電感或者電抗元件，且I(t)為頻率很低的時變值時，電路中的電阻與電抗元件將分別近似于斷路和通路而失去作用，此時電路產生的總干擾磁場仍具有近似的方向確定性.

通過以上分析可知，某些類型的電路產生的磁場干擾具有方向確定性.對于其余類型的電路，通過將其各個支路進行分組，作為獨立干擾源看待，也可以使它們產生的干擾磁場各自具有方向確定性.含有多個電源的更復雜電路也可以按照前面的思路進行分析與分解.

對于地磁場進行分析就簡單得多了.在同一位置，當載體姿態相對地理坐標系發生改變的時候，地磁場與傳感器敏感軸的夾角也會相應發生變化，故要應用ICA，載體是不可以進行滾轉、俯仰等機動運動的.同時，隨著空間位置的變化，地磁場的磁傾角與磁偏角也會發生變化，它所產生的影響可以從2個方面來分析.

首先，根據IGRF2000模型計算主磁場磁偏角與磁傾角的變化趨勢，可發現磁傾角與磁偏角的角度變化非常緩慢.例如，在E70N40位置，磁傾角沿緯度線方向每100 km變化0.983 9°，沿經度線方向每100 km變化0.488 5°，而磁偏角沿緯度線方向每100 km變化0.338 2°，沿經度線方向每100 km變化0.111 2°.故載體在較短的路徑內保持平飛時，主磁場的方向變化是非常微小的.

其次，由于余弦函數在角度為0附近導數最小，如果在數據收集階段，令傳感器敏感軸近似平行于當地的主磁場方向，可以令主磁場的投影波形受磁傾角磁偏角變化的影響進一步減少.可以在開始進行信號收集之前，根據慣導輸出的位置來估計當地磁偏角和磁傾角的值，然后根據這個值調整傳感器的敏感軸方向，并在數據收集階段始終保持敏感軸相對載體方向不變.

通過前面分析，由式(2)與(4)得在單一串聯電路干擾源條件下磁場信號的線性疊加公式為

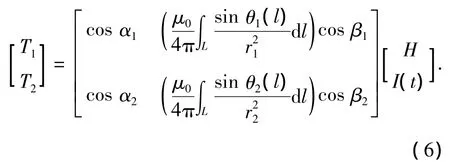
與式(6)類似，可以推出當干擾電路的n個支路被各自作為獨立干擾源時(即符合第二種情況)的信號疊加模型為

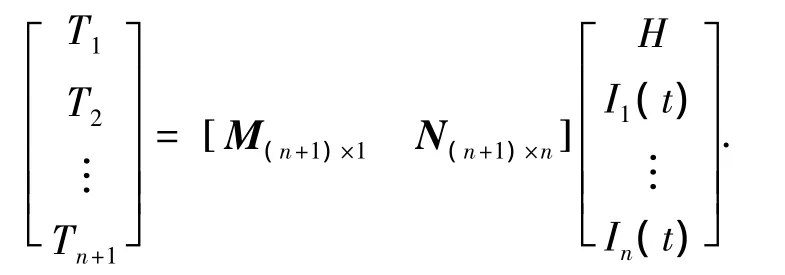
其中

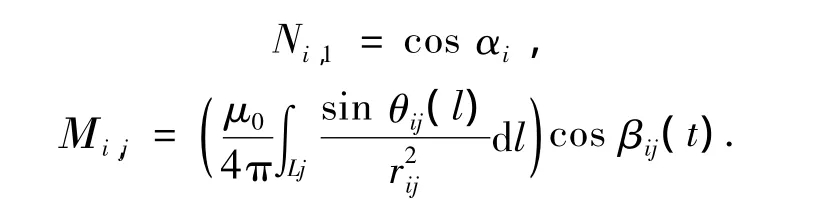
此時，總信號源個數為n+1個，角標i=1，2，…，n+1，j=1，2，…，n，αi代表地磁場與第i個傳感器敏感軸的夾角，為接近0的微小量;βij為第j個干擾源產生的磁場與第i個傳感器敏感軸的夾角，為固定值，由傳感器與干擾源支路的空間相對位置決定;rij為第j個干擾源導線l處的導線微元與第i個傳感器之間的矢徑;θij(l)為第j個干擾源在l處的導線微元與rij的夾角.不同支路分組的情況下的疊加公式可由讀者自行推導，受篇幅所限這里不再贅述.

2.2 克服信號分離后結果的不確定性

當ICA可以被實施之后，下一步的問題就是如何克服ICA分離出的信號的不確定性問題.由于ICA方法的含混性，有2個問題需要解決，首先由于順序上的含混性，無法直接獲知所分離出來的波形結果中哪個是地磁場的測量值，哪些是干擾磁場測量值.其次，即便解決了前一個問題，分離后的結果與實際波形之間的關系是先在幅值上乘以系數然后進行平移的關系，引入相關系數的絕對值，即

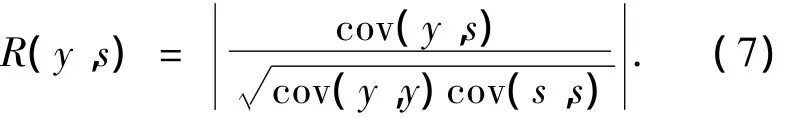
其中cov為協方差函數，R的取值位于［0，1］之間.可以證明，當y與s代表2個波形圖像的幅值時，y與s在圖形上越相似則R的取值越大，如果s與y為線性變換關系，R的值為1.

在沒有任何關于磁場信號波形先驗信息的情況下，只能用所有分離后的波形信號在慣導系統所指示的路徑附近區域內進行搜索匹配，這一點與基于TERCOM的導航定位方法相似.其中能令R取最大值的路徑即為載體經過的實際路徑，對應的波形也就是分離后的地磁場信號波形.

2.3 信號分離與匹配的總體方案

基于前面的分析與推導，提出最終方案如下:首先要對所有電氣設備干擾源進行分析，對于高頻干擾源采用傳統濾波器處理，對于低頻干擾源，按前述方法對電路特性進行區分，獲取主要干擾源的數目，并布置相應數目加1個傳感器.在載體飛行過程中，按照如下步驟進行信號分離和地磁導航定位:

1)準備階段.當發現載體的慣性導航系統輸出位置明顯偏離實際位置時，準備進入數據收集階段，此時根據慣導輸出位置估計當地主磁場方向，并據此調整傳感器的敏感軸方向.

2)數據收集階段.載體保持平飛，實時記錄各個傳感器敏感軸上的磁場信號.

3)信號分離階段.對獲得的信號采用適當的ICA方法進行波形分離.

4)搜索匹配階段.用所有分離后的信號波形在地磁圖上慣導輸出路徑的附近采用式(7)進行搜索匹配，能令相關系數最大的信號波形和路徑即為地磁信號波形和載體的實際路徑.

5)校正階段.根據前面匹配結果，修正慣導系統累積誤差，載體脫離平飛狀態，可自由機動.

3 仿真與結果分析

地磁異常采用2007年7月第24屆UGG大會發布的全球地磁異常圖(WDMAM)中歐洲部分中地磁異常劇烈區域數據作為標準參考［12］.從磁圖矩陣網格中抽取一行的一部分作為實測地磁數據.仿真中的干擾電路如圖1所示.圖中電路采用2 Hz的低頻交流電壓源，并具有3個支路，對應電流i1、i2、i3.由于含有容抗性器件，根據前面的分析，這3個支路可看作是3個獨立的干擾源.數據收集階段所經過路徑上的地磁信號波形，以及3個干擾源對應的電流值如圖2所示.圖3為在4個磁傳感器敏感軸方向上分別檢測到的磁場波形，為地磁場與干擾場在敏感軸向上投影的疊加.

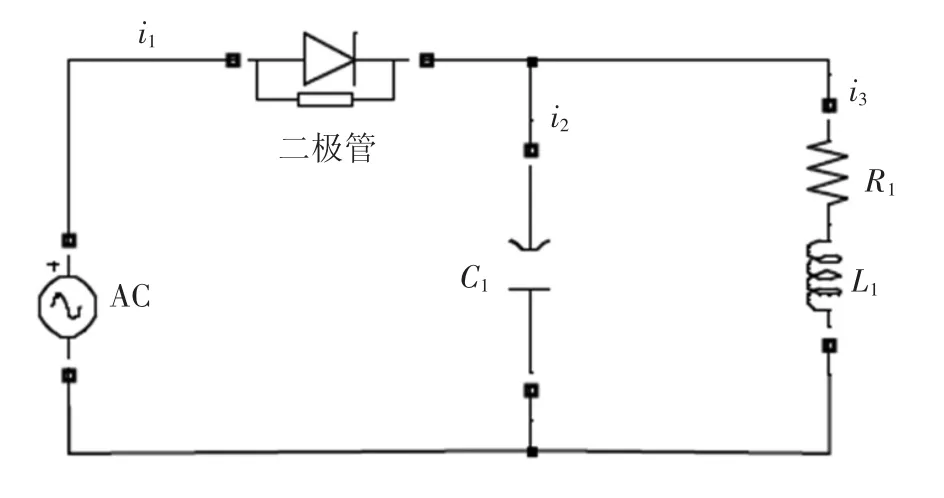
圖1 仿真實驗中所用到的干擾電路

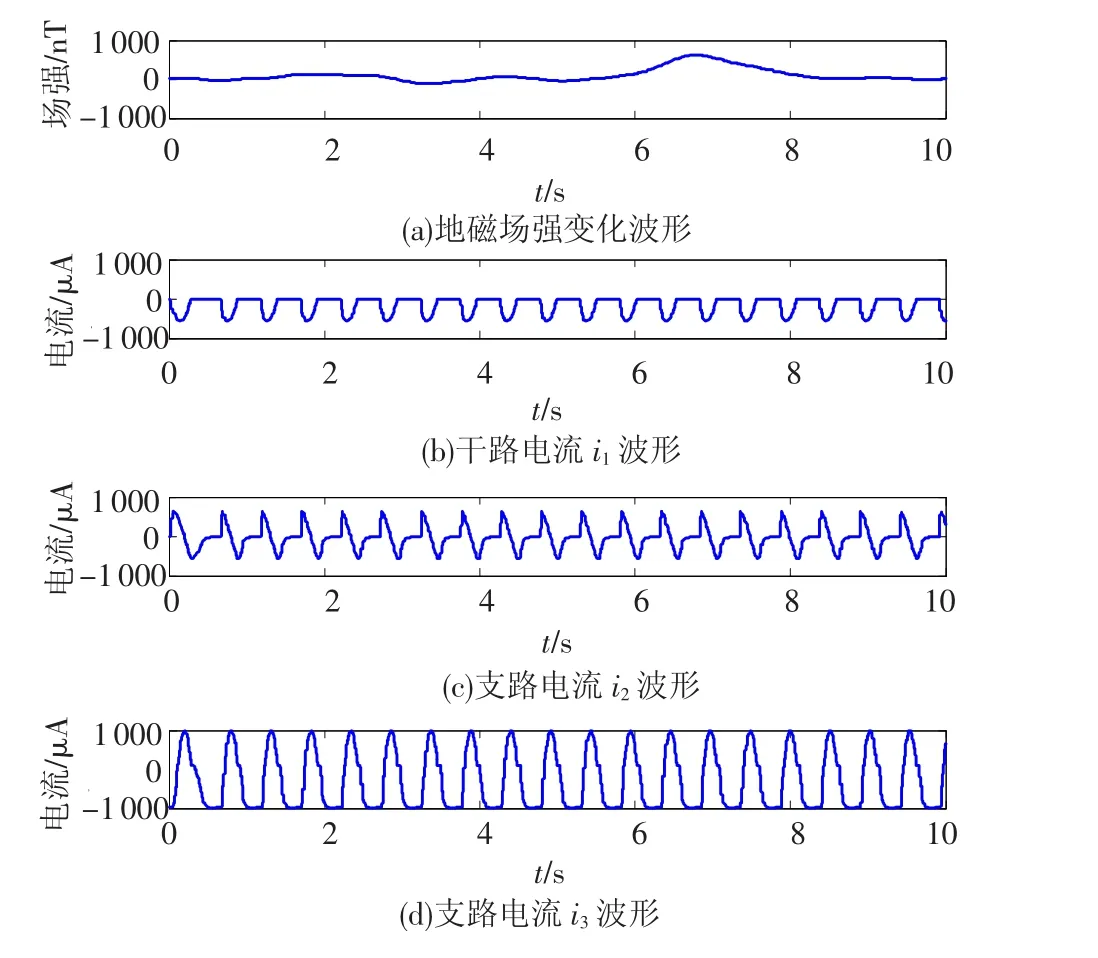
圖2 實際地磁場強波形和干擾電路各支路的電流波形

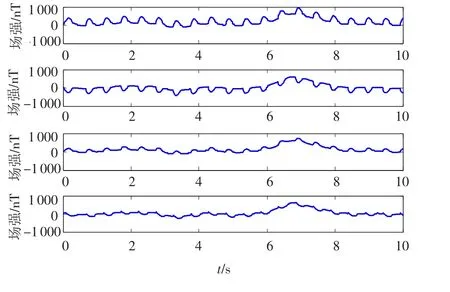
圖3 在3個傳感器上的混疊后信號波形

采用ICA中的定點法(FPICA)進行信號分離，為了驗證其魯棒性，加入了標差為0.1 nT的傳感器測量噪聲.分離后的信號波形如圖4所示(由于ICA方法的幅值不確定性，圖4并未給出縱坐標):

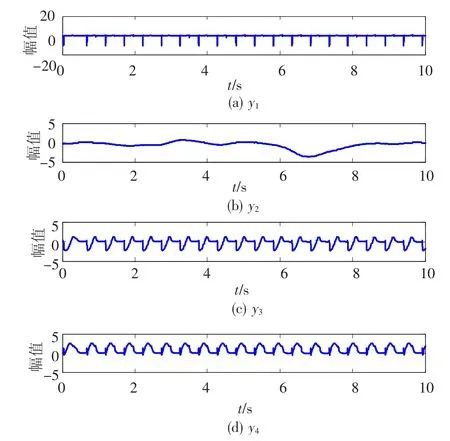
圖4 分離后的信號波形

從圖中可以看出，分離后的4個波形y1、y2、y3和y4雖然與原始波形幅值不同，但是在形狀上保留了較大的相似度，相當于是對原始波形進行了平移、壓縮、以及翻轉.用肉眼觀察可以發現分離后的波形信號與原始信號的對應關系，即地磁信號對應y2，i1對應y1，i2對應y3，i3對應y4.

這里需要指出的是，電流波形分離后形狀上的失真度較大，而地磁信號波形分離后形狀上的失真度較小.造成這種現象的原因是三路電流之間具備一定的相關性(頻率相同，且干路電流i1的幅值為2個支路電流i2和i3的和)，而地磁場信號與3個電流卻是完全獨立的.

采用相關系數絕對值進行相關度驗證.這里用H代表載體運動路徑上的真實地磁信號，用分離后的4路信號波形分別與H通過式(7)計算相關度，可得

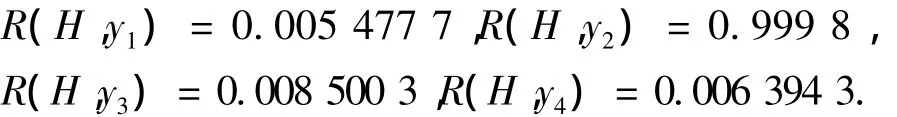
顯然y2與H相似度最高.

進一步，用相似度最大法則在整個區域范圍內進行匹配，匹配后的結果如圖5所示，圖中橫線為實際路徑，圓圈為匹配結果，兩者吻合的非常好.

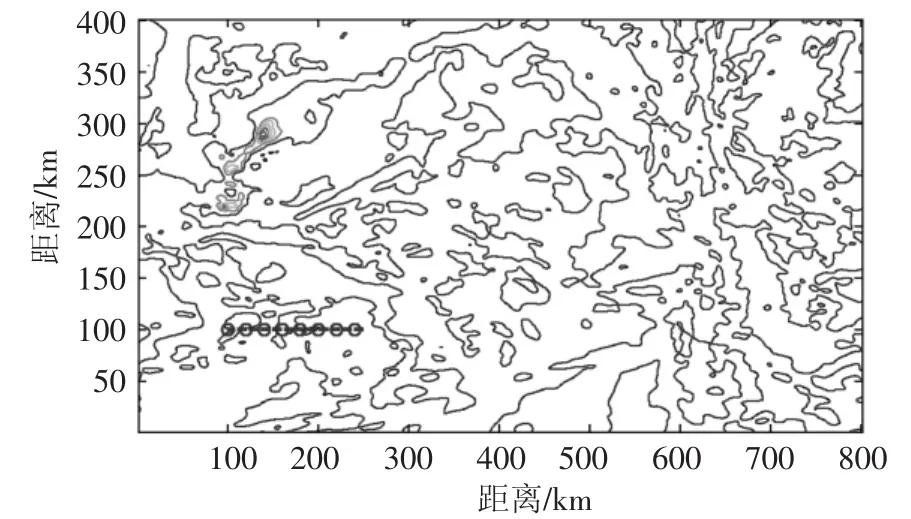
圖5 相關匹配結果

4 結論

本文針對地磁導航技術提出了一種克服低頻電氣干擾源影響的解決方案.理論分析與仿真表明，本方案可有效克服傳統ICA方法應用于地磁導航中所遇到的2個主要障礙，即線性化疊加前提無法滿足，及分離后的信號存在模糊性而難以精確匹配.本文提出的電路電磁特性分析法，是本方案能夠得以實施的基礎和關鍵.但在干擾電路結構復雜，造成劃分出的干擾源個數較多的情況下，可能造成計算量過大，匹配花費的時間過長的問題，這還需要在下一步的研究中進一步完善.

［1］涂有瑞.飛速發展的磁傳感器［J］.傳感器技術，1999，18(4):5-18.

［2］BICKEL S H.Small signal compensation of magnetic fields resulting from aircraft maneuvers［J］.Aerospace and Electronic Systems，1979，15(4):518-525.

［3］GROOM R W，JIA R，LO B.Magnetic compensation of magnetic noises related to aircraft’s maneuvers in airborne survey［J］.BHL Earth Sciences，2004，2:12-16.

［4］劉曉杰.航磁補償技術研究［D］.長春:吉林大學，2009:5.

［5］袁雪萍，潘加明.電磁屏蔽中的難題——磁場屏蔽［J］.電子質量，2006(10):70-72.

［6］HYVARINEN A，KARHUNEN J，OJA E.Independent component analysis［M］.New York:John Wiley＆Sons，2001.

［7］張建明，林亞平.獨立成分分析的研究進展［J］.系統仿真學報，2006，18(4):992-1001.

［8］CARDOSO J F.Blind signal separation:statistical principles［J］.Proceedings of IEEE，1998，86(10): 2009-2024.

［9］HYVARINEN A，OJA E.Independent component analysis:algorithms and applications［J］.Neural Networks (S0893-6080)，2000，13(4/5):411-430.

［10］楊竹青，李勇.獨立成分分析方法綜述［J］.自動化學報，2002，28(5):762-771.

［11］楊英華，吳英華.基于獨立源分析的過程監測方法［J］.控制與決策，2006，21(10):1190-1196.

［12］KORHONEN J V，FAIRHEAD J D，HAMOUDI M，et al.Magnetic anomaly map of the world(and associated DVD)，scale:1∶50 000 000，commission for the geological.map of the world［M］.1st ed.Paris:［s.n.］，2007.