沖壓發動機加速階段進氣道內動態特性①

孫振華，吳催生

(中國空空導彈研究院，洛陽 471009)

0 引言

目前，先進遠程空射導彈多采用整體式沖壓發動機作為動力裝置，它采用雙用途燃燒室，當助推器工作結束后，助推藥柱燃燒完畢剩下的空間，即可作為沖壓發動機的燃燒室，能大大提高導彈的容積利用率，但這樣就必須在沖壓發動機燃燒室的入口端安裝密封堵蓋，亦稱為進氣道出口堵蓋。在導彈助推飛行階段，進氣道內通道被出口堵蓋封閉，其流動涉及進氣道的一些非穩定工作特性，對整體式固沖發動機的工作有非常重要的影響，有可能導致彈體或沖壓發動機結構破壞。因此，對該階段的動態特性進行研究顯得十分必要。

目前，針對沖壓發動機的動態特性研究多集中在沖壓發動機的燃燒不穩定及進氣道在超臨界和亞臨界狀態下激波運動造成的非穩定工作研究，而對整體式沖壓發動機助推加速過程動態特性研究很少。Fujiwar等［1］分析二維外壓縮超聲速進氣道的激波振蕩頻率，與實驗結果吻合，振蕩頻率同樣隨著質量流量的降低而增加。Nishizawa等［2］數值研究了自由流馬赫數1.64 Ma時，外壓式進氣道在亞臨界狀態下的激波振蕩現象。研究發現，在亞臨界時振蕩流動存在多個峰值頻率。其中，低頻成分來自亞音速擴壓器的聲學共振，高頻成分是由來自楔面上的周期分離流動被吸除造成的，高頻率成分在擴壓器長度增大時消失。Lu P J等［3］數值分析了沖壓發動機進氣道喘振現象。結果表明，喘振來自進口處的局部流動不穩定以及氣室中的聲學振蕩。劉占生等［4］采用數值模擬方法，研究了某超聲速進氣道結構的自激振蕩現象，分析了振蕩時進氣道內流場的變化過程。研究表明，發生自激振蕩時，進氣道中流動產生大幅脈動，造成進氣道壁板結構承受周期變化的氣動載荷，載荷振蕩頻譜中包含多個特征頻率，其與聲模態頻率相重合，表明自激振蕩現象與聲模態的相關性。Sivakumar等［5］采用非穩態的RANS方法，對二維沖壓發動機進行了計算，獲得了燃燒室內不同頻率的壓強振蕩。周紅梅、于勝春等［6－7］采用大渦模擬方法，分析了沖壓發動機燃燒室內湍流渦的產生、發展、脫落與破碎過程，總結了導致壓強振蕩的有關因素，并分析了影響振蕩頻率和幅值的主要原因。秦飛等［8］采用大渦模擬耦合預混燃燒模型，分析了沖壓發動機低頻不穩定燃燒的成因。研究結果認為，漩渦運動耦合非穩態的燃燒熱釋放是激發燃燒室低頻壓強振蕩的重要原因。李強等［9］采用大渦模擬方法，對串聯式沖壓發動機的助推段壓強振蕩進行了數值分析。研究表明，其屬于整體模式的不穩定現象。

針對某整體式固沖發動機助推加速過程進氣道內的動態特性，本文進行了數值仿真和相關風洞試驗研究，分析了相同飛行高度下Ma變化對進氣道內壓強振蕩特性的影響，可為整體式火箭沖壓發動機的設計提供指導。

1 物理模型及計算方法

1.1 物理模型

沖壓發動機的簡化模型如圖1所示。進氣道為頭部兩側進氣方式，在進氣道出口處裝有堵蓋，在整體式固體火箭沖壓發動機處于助推階段時，進氣道堵蓋處于關閉狀態;助推結束后，通過轉級指令將進氣道出口處堵蓋打開，來流空氣通過進氣道進入二次燃燒室，進而轉換為沖壓階段。

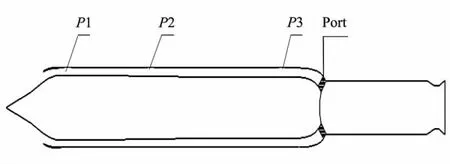
圖1 沖壓發動機簡化模型示意圖Fig.1 Schematic diagram of ramjet engine

1.2 數值方法

計算中，采用有限體積法求解雷諾平均后的三維N-S方程，紊流模型選用Jones和Launder提出的標準k-ε模型，并用一階迎風格式離散。由于紊流模型只適用于離開壁面一定距離的紊流區域，而在與壁面相鄰近的粘性邊界層中，采用的是標準壁面函數修正，時間步長為1×10－4s。計算收斂準則為連續方程、動量方程、能量方程，以及k-ε方程的殘差至少下降3個數量級，且監控點壓強穩定。

本文的研究對象是對稱體，流動也具有一定的對稱性。在不考慮迎角和側滑角組合的情況下，為減少計算量，選取飛行器周圍的一半流動區域作為計算域，計算網格共約205萬網格，網格質量滿足單元內角＞15°，扭轉角 ＜45°，正交性 ＞0.25。分別在進氣道內和補燃室內設置監控點，檢測出口堵蓋打開前后的壓強變化情況。

計算中，用到的邊界條件類型有壓力遠場邊界、壓力出口邊界、對稱邊界和無滑移絕熱固壁等。

1.3 計算狀態

根據不同的飛行狀態，計算進氣道出口堵蓋打開前后的流場特性，計算狀態如表1所示。

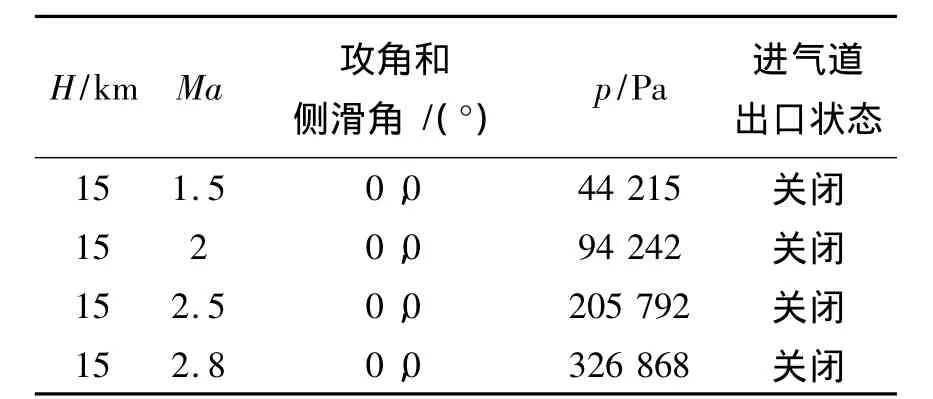
表1 計算狀態Table 1 The calculation cases

2 計算結果與分析

數值計算的研究范圍為Ma=1.5～2.8，主要針對固沖發動機助推加速過程中的典型飛行馬赫數，可得到進氣道出口堵蓋打開前進氣道內的振蕩頻率、幅度及其變化規律。

工況1進氣道內監控點壓強隨時間的變化曲線如圖2所示。

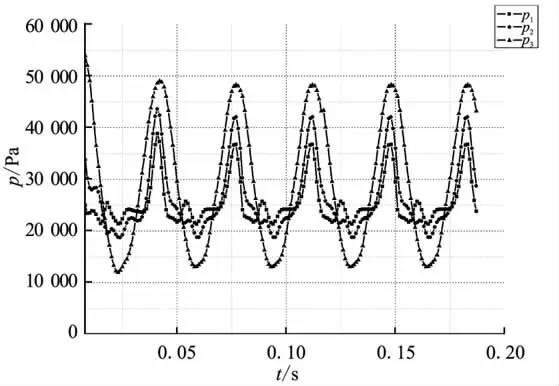
圖2 工況1進氣道內監控點壓強隨時間的變化曲線Fig.2 Time history of pressure oscillation on different inlet monitor points for case 1

從圖2中可看出，各監控點壓強隨時間基本呈正弦規律變化，且進氣道出口處監控點壓強振蕩曲線較平滑;各監控點振蕩相位差較小，即某點壓強處于峰值時，其余各點均接近峰值位置，進氣道內各監控點振蕩接近于整體振蕩模式。分析認為，由于壓強振蕩是擾動傳播引起的，各測點壓強達到峰值點實際時間并非完全一致，但由于測點間距離較小，聲速較大，因此各測點壓強達到峰值時間相距很小，呈現出一種整體振蕩模式。

另外，進氣道沿程各監控點振幅變化不同，進氣道入口附近振蕩幅度較小，進氣道出口附近振蕩幅度較大。分析認為，當進氣道堵蓋沒有打開時，進氣道內通道形成了一個振蕩系統，來流空氣為其提供擾動源，堵蓋作為壓力波的反饋裝置，在進氣道內通道形成穩定的振蕩。在進氣道堵蓋完全封閉的情況下，進氣道整個亞音速通道形成一個擾動反饋裝置，在亞音速通道內，其氣流出現整體振蕩的現象。由于存在氣流進氣道內部堆積和退出現象，在進氣道入口附近，由于存在氣流流動，其本身的壓強是較低的;同時，流動過程使部分氣流脈動得以損耗。因此，其振幅較進氣道出口附近小。

值得注意的是仿真結果表明，進氣道出口處監控點壓強峰值超過來流總壓。分析認為，對于進氣道通道形成的振蕩系統，由于自振是無阻尼的，來流的能量補償了振蕩系統自身的損耗，這種補償是在整個振動周期內進行的，但在一個周期的不同階段，有時能量補償超過了系統自身損耗，有時相反，能量的補償和損耗在一個周期內整體上得到平衡，這就造成了當能量補償超過系統損耗時，監控點壓強峰值會出現超過來流總壓的情況。

工況2～4進氣道內監控點壓強隨時間的變化曲線如圖3～圖5所示。

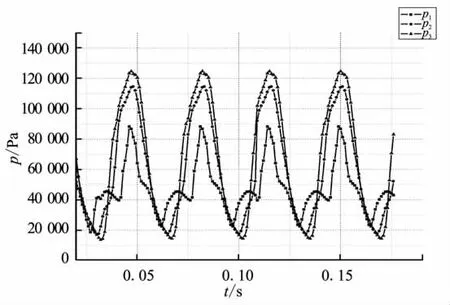
圖3 工況2進氣道內監控點壓強隨時間的變化曲線Fig.3 Time history of pressure oscillation on different inlet monitor points for case 2

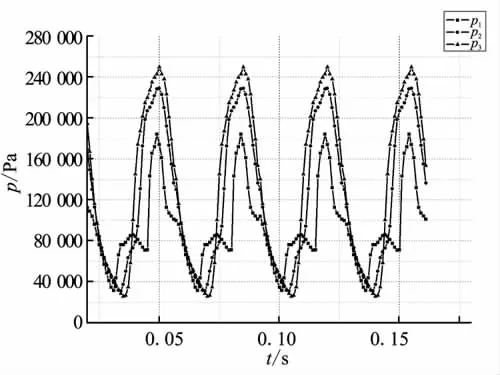
圖4 工況3進氣道內監控點壓強隨時間的變化曲線Fig.4 Time history of pressure oscillation on different inlet monitor points for case 3

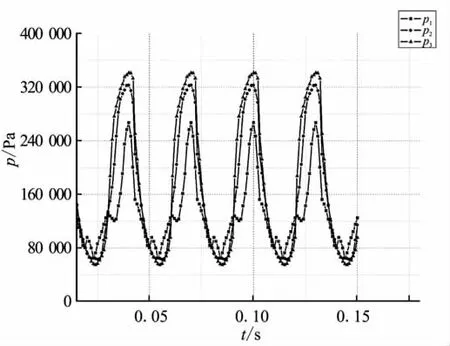
圖5 工況4進氣道內監控點壓強隨時間的變化曲線Fig.5 Time history of pressure oscillation on different inlet monitor points for case 4

從圖3～圖5中可看出，其基本現象與工況1相似，監控點壓強變化規律也與工況1一致，僅振蕩頻率和振幅與工況1稍有差別。這主要是由于對于不同的來流馬赫數，即不同的能量輸入，振蕩系統的反饋速度和響應幅度不同。

圖6為不同馬赫數下各監控點壓強相對振蕩幅度計算值對比圖。結果表明，各監控點的壓強相對振蕩幅度隨馬赫數增大而下降，進氣道內不同位置處壓強相對振蕩幅度不同，越接近出口堵蓋處，壓強相對振蕩幅度越大。

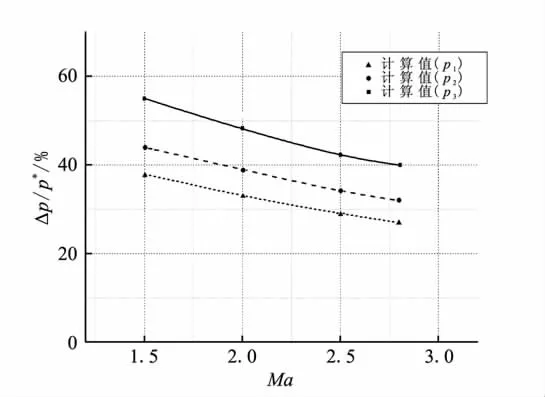
圖6 不同馬赫數下各監控點相對振蕩幅度計算值Fig.6 Relative pressure oscillation amplitude on different inlet monitor points at different Mach numbers

3 試驗驗證及對比

為進一步準確地獲得助推加速段進氣道內的動態工作特性，本文開展了相關條件下的風洞試驗，試驗模型縮比2.25∶1，進氣道內左右各布置了3路動態壓強傳感器，分別對應于計算監控點位置，檢測其壓強的實時變化過程。

試驗數據的處理采用Danielson-Lanczos方法進行FFT變換，得到壓力振蕩的功率頻譜，離散方法如式(1)所示，功率頻譜計算如式(2)所示。

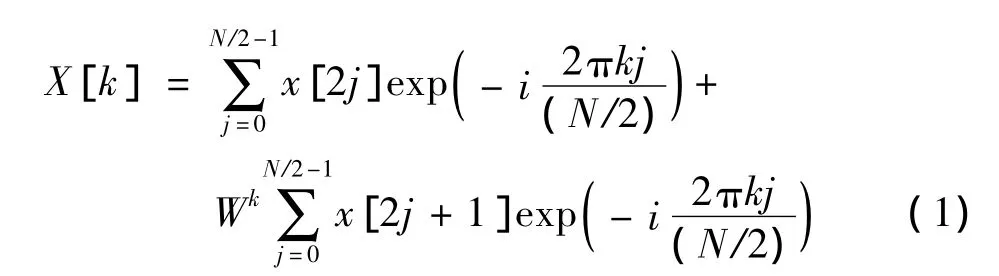
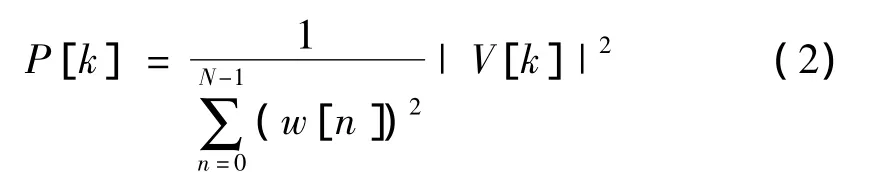
Ma=2.5狀態流道沿程測點壓強動態曲線與頻譜特性如圖7所示。從圖7中可看出:(1)沿通道從前至后，各測點平均壓強依次增大;(2)各測點頻率特性一致，沿通道從前至后，振幅依次增大;(3)在一階頻率處能量較大，其余高階頻率能量低一個量級以上，在實際工程中，可不用考慮其影響;(4)測點3、6的壓強峰值超過來流總壓，這些現象與上述仿真過程中得到的結果吻合較好。

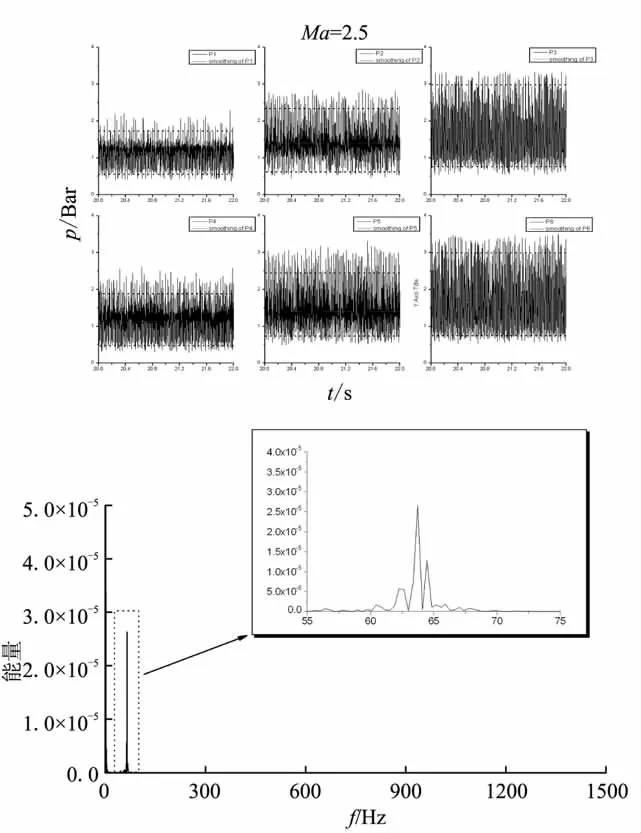
圖7 各測壓點壓強動態曲線及頻譜特性圖Fig.7 Pressure evolution and spectrum characteristics at different measuring points

圖8為Ma=2.5狀態下不同測點的動態壓強測試曲線。從圖8中可看出，進氣道出口堵蓋打開前，進氣道通道內壓強振蕩基本屬于整體模式的不穩定振蕩。

圖9為風洞試驗中不同馬赫數下進氣道壓強相對振蕩幅度對比。結果表明，各測點壓強相對來流總壓的振蕩幅度隨馬赫數增大而下降。進氣道入口附近，壓強振蕩相對幅度較小;進氣道出口附近，相對振蕩幅度較大。以上規律與仿真結果一致。

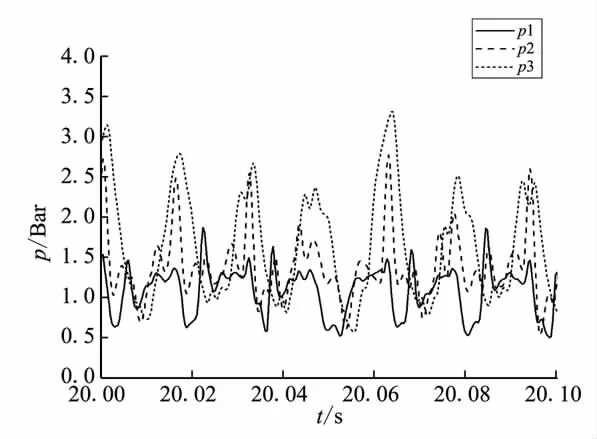
圖8 Ma=2.5風洞試驗不同測點動態壓強變化Fig.8 Temporal variation of pressure at different measuring points for Ma=2.5 wind test

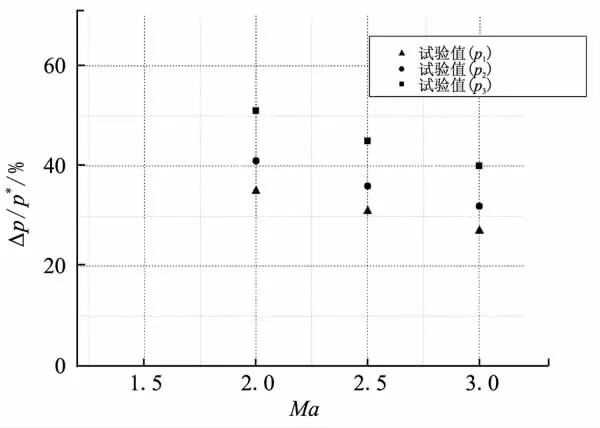
圖9 不同馬赫數下進氣道壓強相對振蕩幅度試驗值Fig.9 Relative pressure oscillation amplitude at different Machs numbers for wind tests

根據相似理論，對試驗數據進行換算處理，得到真實進氣道通道狀態內振蕩頻率值，其隨來流馬赫數變化規律如圖10所示。從圖10中可看出，壓強振蕩頻率隨馬赫數增大略有升高。分析認為，隨馬赫數增大，進氣道通道入口溫度升高。根據聲學共振原理，當地聲速越大，因此共振頻率越高。另外，仿真值與風洞吹風試驗處理值規律較為一致。

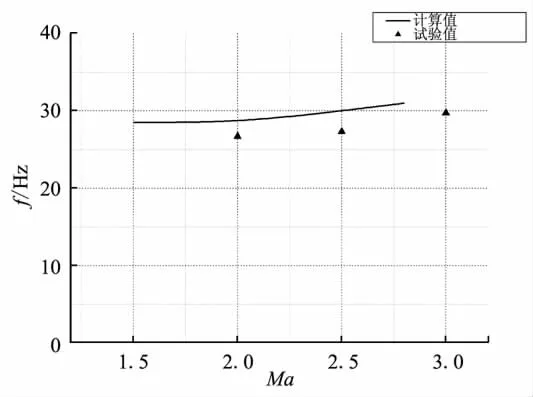
圖10 不同馬赫數下振蕩頻率的試驗換算值與計算值對比Fig.10 Comparison of the pressure oscillation frequency at different Mach numbers between test conversions and simulations

4 結論

(1)助推加速段進氣道通道內，振蕩頻率隨馬赫數增大略有升高，相對振蕩幅度隨馬赫數增大而下降。

(2)進氣道內不同位置處，壓強相對振蕩幅度不同，越接近出口堵蓋處，壓強相對振蕩幅度越大。

(3)在所研究范圍內，進氣道振蕩過程中出現的最高壓強有可能超過來流總壓。在工程應用中，應充分考慮其對進氣道結構的影響。

(4)采用的動態數值仿真方法，能較好預測整體式固沖發動機助推加速段進氣道可能出現的自激振蕩，所得結果及規律與吹風試驗較為一致。

［1］Fujiwara H，Murakami A，Watanabe Y.Numerical analysis on shock oscillation of two-dimensional external compression inlets［R］.AIAA 2002-2740.

［2］Nishizawa U，Kameda M.Computational simulation of shock oscillation around a supersonic air-inlet［R］.AIAA 2006-3042.

［3］Lu P J，Jain L T.Numerical investigation of inlet buzz flow［J］.Journal of Propulsion and Power，1998，14(1):90-100.

［4］劉占生，張云峰，田新.沖壓發動機超聲速進氣道流動自激振蕩研究［J］.航空動力學報，2008(9).

［5］Sivakum arR，Babu V.Numerical simulation of low frequency pressure oscillations in a model ramjet combustor［R］.AIAA 2005-2911.

［6］周紅梅，于勝春.沖壓發動機燃燒室內的壓強振蕩研究［J］.飛航導彈，2006(4).

［7］于勝春，周紅梅.突擴燃燒室低頻壓力振蕩的大渦模擬［J］.海軍航空工程學院學報，2006(5).

［8］秦飛，何國強，等.同軸突擴燃燒室低頻不穩定燃燒數值模擬［J］.推進技術，2008，29(4).

［9］李強，劉佩進，李江，等.沖壓發動機助推段壓強振蕩現象數值分析［J］.推進技術，2008，29(6).