金融市場的波動溢出效應模型及實證

黎娜

（滁州學院 經濟管理系，安徽 滁州 239000）

0 引言

對于開放的資本市場，不同資本市場之間在信息傳播、資金流動、市場運作等方面的聯系不斷加強，使得各市場之間的關系日益緊密，不同市場之間的收益越來越具有同向運動的特征，存在不斷整合的趨勢。一個資本市場上的波動不僅受自身過去波動的影響，往往也會受其他市場波動的影響，這種市場間波動的傳導關系為波動“溢出效應”。兩個市場的波動溢出效應是指不僅兩市場要受過去幾期自身波動的制約,而且要受到對方市場波動的顯著影響。波動溢出效應可能存在于不同地域的市場之間，也可能存在于不同類型的市場之間，如股票市場、外匯市場、債券市場之間等。不同市場之間的波動可能存在著相互影響，波動會從一個市場傳遞到另一個市場。國內外學者對股票市場波動性的研究主要包括:Mukherjee和 Mishra使用簡單的GARCH(1,1)模型研究了印度和亞洲12個主要與其交易的國家之間的股市一體化和波動溢出效應。Bhar和Nikolova采用二元EGARCH模型分析了金磚四國股市的收益率、波動溢出性和動態相關性；張志聰和徐之煒采用GARCH(1,1)模型,研究了滬深A股指數收益波動的特性,并探討了兩市波動的相關關系；谷耀等采用DCC模型研究了滬、深、港三地股市的溢出效應與動態相關性。

本文針對研究金融市場溢出方法存在的缺陷，引入因子分析法來消除多個金融市場波動之間的相關性，通過使用構建的雙變量EC-EGARCH模型來研究波動溢出問題，以探究這些市場之間的關聯性和波動溢出效應。通過計算出深圳證券市場的VaR值，最后取2005年8月1日至2010年8月1日期間的上證綜指、深圳成分指數、香港恒生指數、新加坡海峽指數、日經指數為原始數據進行了實證分析。

1 波動溢出效應模型的構建

1.1 雙變量EC-EGARCH模型

研究多個金融市場對一個金融市場的共同波動溢出，首先對這些金融市場波動數據進行因子分析，用公共因子數據代替這些金融市場波動數據，從而分析判斷多個金融市場對一個金融市場是否存在共同波動溢出影響。EGARCH模型能夠較好的擬合信息對波動反映的不對稱性以及相關市場間的波動溢出效應，并且該模型對參數沒有約束限制。協整殘差項反映了金融市場指數之間長期穩定的關系，為了考察一個金融市場的協整殘差項對其他金融市場的溢出效應，構建雙變量EC-EGARCH模型。構建EC-EGARCH(1,1)模型如下：

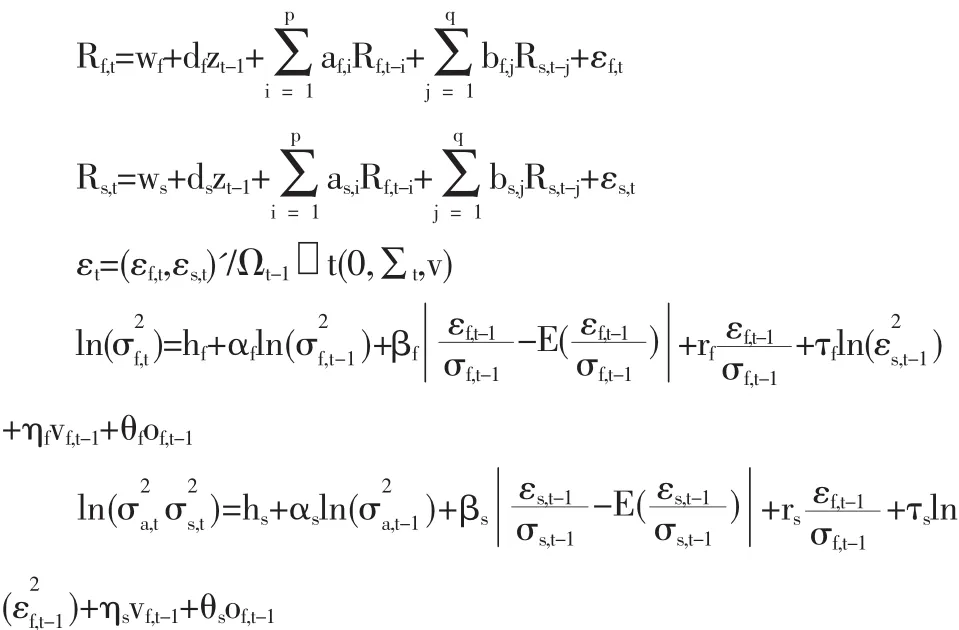
在條件均值方程式中,Rf,t=Cf,t-Cf,t-1，Rs,t=Cs,t-Cs,t-1，誤差修正項zt-1為解釋變量,Ωt-1為t-1時刻的信息集，∑t為二階的時變條件協方差矩陣,h為常數項；εf,t和εs,t分別為條件均值方程的殘差；α為滯后一階的對數方差項的系數，用來描述波動的集聚性和持續性；β和r可以用來描述信息對波動的影響程度，并且系數r可以反映波動對信息反應的杠桿效應；系數τ表示一個市場對另一個市場的波動溢出效應；至此完成了構建EC-EGARCH模型的條件均值方程和條件方差方程。

1.2 參數估計方法

2 實證結果及分析

2.1 樣本的選取

選取2005年8月1日至2010年8月1日期間的上證綜指、深圳成分指數、香港恒生指數、新加坡海峽指數、日經指數為原始數據。（數據來源：萬得數據庫和中國債券信息網）。由于不同股市指數的基數不同，將股票指數轉換為日對數收益率Rt=ln(Pt/Pt-1)，其中P為股票指數。由于每個地區時差及節假日的不同，對原始數據進行預處理，最終每個股票市場得到1236期數據。

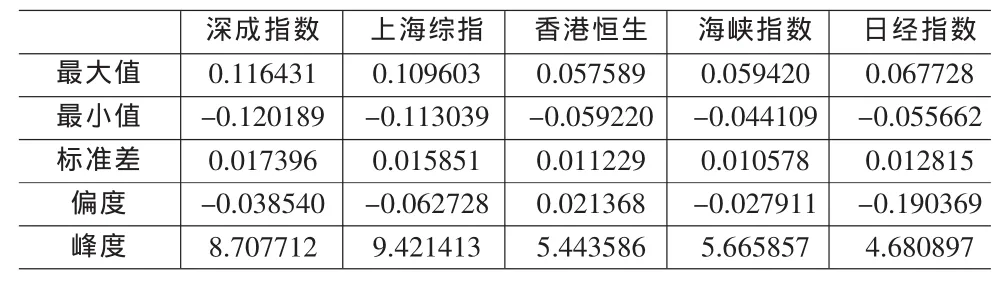
表1 五個指市場指數的描述統計量

在整個樣本期間，我國股市有更大的標準差，最大值與最小值之差也最大；所有股市日收益率都存在偏度，其中上海綜指偏度最大，深成其次；所有股市日收益率的峰度均大于3，這說明所有股市日收益率分布都呈尖峰厚尾特征（見表1）。

2.2 股市收益率波動計算與Granger因果檢驗

根據上述方程分別對各股票市場日收益率數據分析建模并進行參數估計。應用Eviews5.0軟件計算出模型的參數估計值，進而估計出各股票市場日收益率的方差，通過估計出的模型計算出各股市日收益率的方差序列為}分別代表深圳成指，上海綜指，香港恒生，海峽指數，日經指數收益率的方差序列。采用Granger因果關系檢驗來判定深圳成分是否與其他各股票市場存在波動溢出，檢驗結果如表2至表5

從Granger因果檢驗結果分析表明：對深圳成分指數的波動性有明顯影響的股票市場是上海綜指、新加坡海峽指數、香港恒生指數，這是因為這幾個市場對深圳成分指數的影響的Probability值分別為0.00598，0.00956，0.01932。日經指數對深圳成分指數的影響Probability值為0.65221遠大于0，對深圳成分指數的波動性幾乎沒有影響。

表2 深圳成分、上海綜指的Granger因果檢驗結果

表3 深圳成分、日經指數的Granger因果檢驗結果

表4 深圳成分、海峽指數的Granger因果檢驗結果

表5 深圳成分、恒生指數的Granger因果檢驗結果

2.3 波動溢出判斷

根據前面的波動溢出判斷得到上海綜指，新加坡海峽指數，香港恒生指數三個市場對深圳成分指數有明顯影響，但是這三個市場之間有可能存在相關關系，采用因子分析法消除它們之間的相關關系。因子分析是通過對原始數據相關系數矩陣內部結構的研究，將多個指標轉化為少量互不相關且不可觀測的隨機變量(即因子)，以提取原有指標絕大部分信息的統計方法。當因子載荷陣結構不夠簡化時，可以通過因子旋轉使因子具有更為鮮明的實際意義，同時使用因子得分函數對樣本給出相應的評價和排序。因子分析的數學模型為：X=AF+ε

X=(X1,X2,…,Xp)'為原指標，F=(F1,F2,…,Fm)'為X的公共因子，A為因子載荷矩陣，ε為特殊因子。論文使用主成分因子提取方法，其特點在于可以用方差貢獻值βi衡量第i個公因子的重要程度。因子分析步驟如下：

①將原始數據標準化，仍記為X；②建立相關系數矩陣R；③解特征方程|R-λE|=0，計算特征值和特征向量，當累計貢獻率不少于85%時，取前k個主成分代替原來的m個指標，計算因子載荷矩陣A；④對A進行最大正交旋轉變換；⑤對主因子進行命名和解釋。如需進行排序，則計算各個主因子的得分Fi=αix，以貢獻率為權重，對Fi加權計算綜合因子得分。

因子分析法分析結果如表6所示。

選取兩個因子時，累計貢獻率達到了93%以上，所以我們選擇兩個主因子F1,F2。通過因子分析法得到F1,F2兩個主因子，帶入到方程進行參數估計，使用Eviews5.0軟件計算出參數的估計值，結果如表7所示。

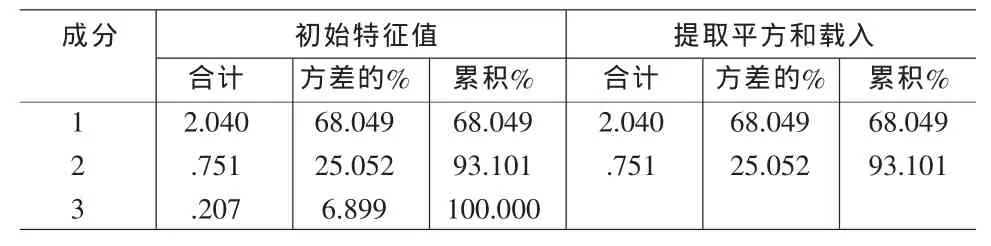
表6 因子分析結果

表7 參數估計結果

3 結論

本文采用構建的雙變量EC-EGARCH模型結合因子分析法和VaR計算研究了多個證券市場對深圳證券市場的共同波動溢出問題，結果表明新加坡海峽指數，香港恒生指數，上海綜合指數波動對深圳成分指數影響比較顯著，存在共同波動溢出效應。將共同波動溢出效應添加到計算VaR的模型中去，通過此模型計算出的VaR將更能符合實際情況，期望方程和方差方程中各回歸項的系數都在1%的水平下顯著不為零，進一步驗證了模型設定的科學性。

[1]Mukherjee,K.，Mishra,R.K.Stock MarketIntegration and Volatility Spillover:India and its Major Asian Counterparts[J]. Research in International Business and Finance,2010,(24).

[2]Bh ar,R.，Nikolova,B.Return,Volatility Spillovers and Dynamic Correlation in the BRIC Equity Markets:An Analysis Using a Bivariate EGARCH Framework[J].Global Finance Journal,2009,(19).

[3]Tully,E.，Lucey,B.M.A Power GARCH Examination of the Gold Market[J].Research in International Business and Finance, 2007,(6).

[4]喬海曙,陳志強.我國滬深A股市場板塊波動現象研究[Z].第四屆中國金融學年會論文，2006.

[5]張瑞鋒,張世英.基于VS-MSV模型的金融市場波動溢出分析及實證研究[J].系統工程,2007,(8).

[6]王璐等.中國股市和債市波動的溢出效應——基于交易所和銀行間市場的實證研究[J].金融論壇，2008,(4).

[7]陳云,陳浪南,林魯東.人民幣匯率與股票市場波動溢出效應研究[J].管理科學,2009,(3).

[8]谷耀,陸麗娜.滬、深、港股市信息溢出效應與動態相關性——基于DCC-(BV)EGARCH-VAR的檢驗[J].數量經濟與技術經濟研究,2008,(8).