風險價值法VaR對套利風險的衡量研究

景 楠

（西安外國語大學 商學院，西安 710000）

在期貨套利交易中，投資者最關心的問題，莫過于建倉之后到平倉退出之前這段持有期內如何規避風險。由于投資者存在大量未結清的頭寸，在持有期內其頭寸價值的變化將導致收益的變化，同時也直接影響到所占用保證金的變化。

為了從數量上衡量和控制套利交易的風險，我們試圖引入西方現代風險管理方法VaR，對投資者對手中所持有的套利交易資產組合的風險價值在一段時間內或者每天進行估值和計量，將計算出的風險大小與自身對風險的承受能力加以比較，以此來決定投資額和投資策略，及時調整套利資產組合，減少投資的盲目性，從而達到分散和規避投資風險，盡可能地減少因投資決策失誤所帶來的損失。

1 VaR計算的方法選擇

本文主要以金屬期貨跨市套利投資組合的風險進行定性和一定的定量研究，為投資者的投資提供量化的決策依據。

VaR的計算方法可以分為三種：

(1)方差協方差法。這是最簡單的方法，它假設資產收益率是風險因素的線性（或德爾塔）函數，并認為風險因素是正態的，并運用期望值和方差獲得VaR結果。但是，一旦某資產的回報率是非正態分布的，其計算的結果就會出現偏差。

(2)歷史模擬法。歷史模擬法提供了一種簡單直觀、易于解釋的完全估值方法，根據實際價格估計，這個方法允許非線性和非正態分布，不需要確切知道合約價格、收益的分布函數。其完全估值是通過歷史數據來實現的，它不需要對定價模型和市場的隨機結構做出某種特定的假設。它也考慮了“厚尾”問題，而且不依賴于特定的定價模型，因此，歷史模擬法一般不會出現模型風險。

(3)蒙特卡洛模擬法。相對而言，這一方法在概念上和計算上比較復雜，對電腦資源的要求也很高,因此在應用上沒有前兩種方法廣泛。當投資組合較為龐大時，很可能會由于硬件限制而無法完成計算。這種方法建立在投資組合收益可供允許簡單模擬的基礎之上，生成基于既定概率分布之上的隨機結果，從而獲得VaR的值。

在對上述方法作出權衡的基礎上，我們選取歷史模擬法來計算VaR。

在計算期貨頭寸VaR的過程中，要確定一個套利資產組合的VaR值必須首先要確定以下兩個參數：一是持有期間的長短；二是置信度的大小。實際上還有第三個，就是觀測期間。因為從不同的期間觀察，VaR的值是不一樣的。

持有期間是一項基本因素，在其余方面相同的情況下，10天的VaR比1天的VaR要大。對于持有期間的選擇與金融機構或投資機構的業務種類和所分析的資產組合有關。頭寸的持有期限究竟選擇1天、2天，亦或更長的時間，同測量者的偏好相關。對于流動性比較大的資產組合，最好選擇1天的時間段。比如對于需要按季度調整組合并報告業績的投資銀行業務來說，90天是比較合適的。理想的情況是，持有期與投資組合定期清算所需的最長時間相一致為宜。

置信度越大，VaR就越大，一旦發生損失，則損失的額度就越大；置信度越小，VaR就越小，一旦發生損失，則損失的額度就相對較小，但也存在可能低估在極端情況下出現的損失。5%或1%的概率是否可以被視為“小概率事件”或“極端情形”呢，從風險控制的角度來看，這只是個選擇的問題（JP摩根銀行在計算VaR時使用的是95%的置信水平）。置信度的選擇與風險管理者處理小概率事件的能力以及期貨經紀公司對客戶爆倉損失的容忍程度有關。風險管理者的應變能力比較強，期貨公司對損失的容忍度比較大，就可以選擇比較高的置信度，也就是選擇比較低的保證金水平。比較低的保證金能給期貨公司帶來競爭力，從而有利于提高傭金收入。對于個人投資者而言，也可以通過由期貨公司或投資機構提供的不同置信度區間下的VaR值，來判定手中所持有的投資組合是需要繼續持有還是平倉止損。

作為一個統計數值，VaR的值是隨著時間的推移而變化的。在上述兩個參數不變的情況下，如果市場波動趨于活躍，那么VaR的值應當變大；如果市場波動趨于平緩，那么VaR的值應當縮小。這就要求我們在使用VaR方法的時候要及時重新計算VaR值，觀察期間當然要包括最新的市場數據，并適當回溯歷史。在選擇觀察期間長度的時候，既要考慮保持VaR值的穩定性，又要使其能更多的反映市場最新的變化。

目前國內在期貨領域應用VaR方法主要局限于計算合約單邊頭寸的VaR（比如石油期貨等）方面，涉及期貨合約投資組合VaR的相關論文則并不多見。本文主要從套利投資組合的角度來研究期貨合約的VaR，通過套利投資組合的VaR與單邊頭寸VaR的比較，可以使投資者對于哪一種是較低風險的投資策略一目了然。由于套利組合的VaR值能夠把對預期的未來損失的大小和該損失發生的可能性結合起來，所以它不僅可以使投資者能夠明白發生損失的規模，而且知道損失發生的可能性。

2 套利投資組合以及單邊頭寸的VaR（平均）衡量公式

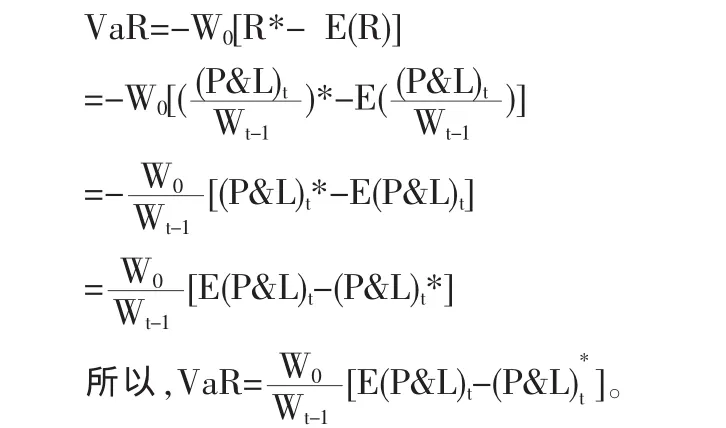
據上式，套利投資組合的風險價值為：

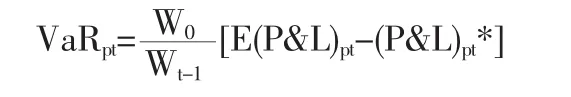
風險價值有絕對風險價值和相對風險價值。本文主要探討相對風險價值。對于一般分布的資產而言，相對風險價值的計算公式為 VaR[5]（平均）=E(W)-W*，其中，W＝W0（1+R）表示資產的價值，W*=W0（1+R*）表示在給定置信水平下資產的最小價值，W0為初始投資額，R為資產的收益率。

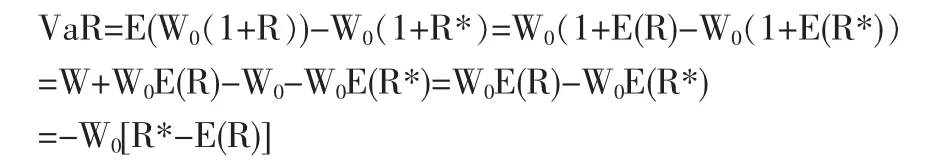
對于期貨合約而言，最容易獲得的數據是合約的浮動盈虧即收益而不是合約的收益率。浮動盈虧包括浮動盈利和浮動虧損，浮動盈虧能夠反映期貨頭寸的價值變化。浮動盈利越小(浮動盈虧越大)，期貨頭寸的價值就越低；頭寸最小價值正好同頭寸的最大浮虧相對應。事實上，在計算VaR的過程中，引入浮動盈虧或者頭寸收益較收益率更為直觀，能夠大大縮小計算量，有效降低運算成本，但數據的精確性并不會受到影響。

持有期為1天的期貨合約投資收益率可以定義為當日合約的浮動盈虧同前一天的合約價值之比或當日合約的浮動盈虧同當天的保證金之比。本文采用前者進行定義，所以，期貨頭寸的收益率為投資組合價值建立的倫銅單邊頭寸風險價值為：

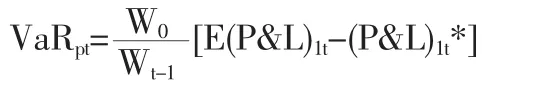
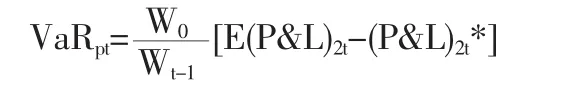
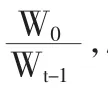
投資組合價值建立的滬銅單邊頭寸風險價值為：所以決定風險價值比較結果的因素為方程左邊的第二個因子，那么，風險價值可以作如下變化：

套利投資組合的風險價值記為：

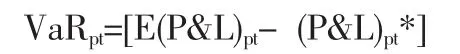
投資組合價值建立的倫銅單邊頭寸風險價值記為：

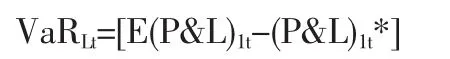
投資組合價值建立的滬銅單邊頭寸風險價值為：

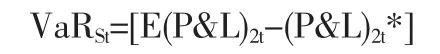
如果去掉時間下標，上述三公式為：

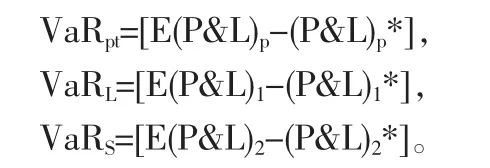
根據上述公式計算出的結果將是持有期為1天的VaR。如果持有期為2天、3天、30天或者更長的時間，那么就需要重新計算，因此，對于投資者而言，風險價值必須每天作一次新的記錄并長期觀察，才能在一段指定的持有期或觀測期內比較風險價值VaR是否出現較大的變化。

3 實例分析

我們主要以金屬期貨市場上最常被投資機構和投資者采用的期銅正向跨市套利交易投資組合、倫銅多頭、滬銅空頭為例，具體說明如何計算基于頭寸價值的單邊頭寸VaR的原理和步驟（這里倫銅系指倫敦金屬交易所銅標準期貨合約，滬銅系指上海期貨交易所標準銅期貨合約）。

跨市套利是指在某個交易所買入或賣出某一交割月份的某種商品期貨合約的同時，在另一個交易所賣出或買入同一交割月份的同種同樣標的數量的商品合約，以期將來在某個有利時機的在兩個交易所分別對沖持有的合約來獲利。我國的銅期貨套利一般是指在倫敦金屬交易所(LME)買入或賣出某一交割月份的銅期貨合約的同時，在上海期貨交易所(SHEF)賣出或買入同一交割月份的相同噸數的銅期貨合約，以期將來對沖獲利。銅期貨套利有正向套利和反向套利兩種。正向套利是指在倫敦金屬交易所買進期銅合約的同時，在上海期貨交易所賣出期銅合約，將來于某個有利時機分別對沖獲利。反向套利則正好與之相反。

從理論上講，VaR的計算根據不同置信度 （如95%，95.5%，96%，99%等等）的個數C，不同的觀測值數量 （如500，1000，1500等等）的分類N和不同的持有期（如1天，2天，30天，60天等等）的個數H進行計算，共有N*C*H種不同的VaR。考慮到計算成本和典型性，筆者計算幾種有代表性的VAR來說明投資組合以及各頭寸的風險VaR比較。置信度水平選擇95%和99%（即顯著性水平為5%和1%），持有期限為1天，觀測數據的樣本量為1500個。

由于兩類資產之間是負相關的，多空組合能夠更大程度的降低投資組合風險。為了計算上的方便，虛擬一個的基本的套利投資組合，組合的總金額設定為購買一手滬銅空頭合約價格與購買一手倫銅多頭合約價格 （根據即期匯率折算為人民幣）之和。相應的可以求出倫銅和滬銅合約各自所占的權重。同時，投資組合總金額的變動會導致VaR成比例的變動。

由于利率、關稅率、增值稅率、P(t)基本上在一個較長的時期內是相當穩定的，所以我們忽略了這幾項因素以簡化VaR模型。

我們選取1500個觀測值,置信度設為99%，持有期為1天，計算基于浮動盈虧的倫銅多頭和滬銅空頭構成的套利投資組合（正向套利投資組合）、倫銅多頭、滬銅空頭的VaR。

(1)構造基本的倫銅多頭和滬銅空頭套利投資組合

倫銅期貨合約為每手25噸，而滬銅期貨合約為每手5噸，所以，構造一個基本的倫銅和滬銅套利投資組合需要1手倫銅期貨合約和5手滬銅期貨合約，即25噸倫敦期銅和25噸滬銅期貨合約。正向套利基本投資組合是在LME買進1手倫銅期貨合約的同時，在SHEF賣出5手滬銅期貨合約。

根據數據，我們可以構造期銅跨市正向套利投資組合，虛擬套利投資組合由兩個對沖頭寸構造而成，以倫銅折算為人民幣的價格建立1單倫銅多頭合約（為了計算上的簡化全部取整數），標的數量為25噸，同時以上海滬銅的價格建立5單滬銅空頭頭寸，標的數量亦為25噸。

(2)分別計算倫銅多頭和滬銅空頭在投資組合中所占的權重

根據馬科維茨的均值-方差模型，正向套利投資組合的價值公式一般形式

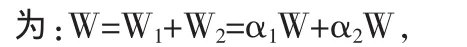
其中，α1＝W1/W，α2＝W2/W，W 表示套利投資組合的價值，W1表示倫銅多頭價值，W2表示滬銅空頭價值，α1表示倫銅多頭在投資組合中所占的權重，α2表示滬銅空頭在投資組合中所占的權重。

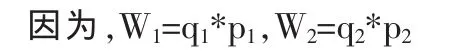
其中，q1，q2分別為倫銅和滬銅的標的數量，單位為噸；p1，p2分別為倫銅和滬銅期貨每噸報價，倫銅的報價是采用匯率調整后的人民幣價格。

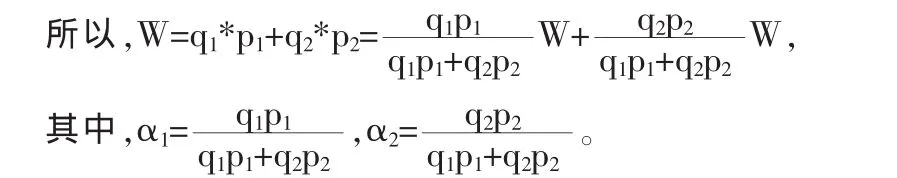
當投資組合的頭寸數量確定之后，也就是q1，q2的值確定后（q1=q2=25噸），那么投資組合的權重只同各合約的價格相關。

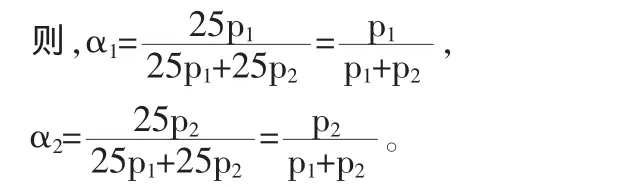
對于上述投資套利組合，其價值為W=q1*p1+q2*p2。倫銅多頭頭寸的權重為α1=[p1/(p1+p2)]，滬銅空頭頭寸的權重為α2=[p2/(p1+p2)]。

采用上述權重公式，我們可以計算出從1996年1月3日到2009年12月31日基本套利投資組合的頭寸權重。頭寸權重的具體數值見圖1

上述頭寸權重圖中，α1的均值為0.45，α2的均值為0.55，因此，在計算投資組合價值構造的單邊頭寸數量的過程中，α1取值0.45，α2取值0.55較為合理。

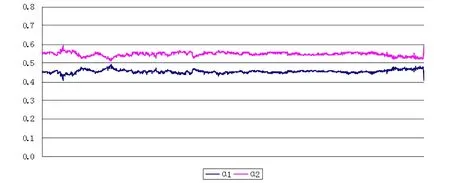
圖1 跨市套利投資組合的頭寸權重表

(3)計算用套利投資組合價值構建倫銅多頭單邊頭寸或滬銅空頭單邊頭寸的數量

用投資組合的總價值所構建的單邊頭寸的數量等于投資組合的價值與單邊頭寸單價的商。所以，倫銅多頭和滬銅空頭的單邊頭寸數量頭寸的數量計算如下：

因此，倫銅多頭單邊頭寸數量：

滬銅空頭單邊頭寸數量：

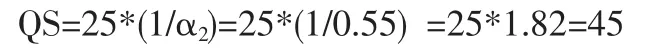
這一計算的意義在于當求出每噸或一份合約的風險價值VaR之后，可以運用上述關系求出單邊頭寸的VaR。

4 結論

從以上實例分析可知，VaR主要適用于正常市場條件下對于市場風險的衡量，由于統計模型預測值的準確性在很大程度上取決于有效歷史數據的充分性，因而對數據有較為嚴格的要求。在正常市場條件下，資金的交易數據比較豐富，使用VaR模型較為有效，而當市場遠離正常狀態時，資產價格的關聯性被割斷，流動性全部消失如爆發金融危機或發生期貨市場事件時，使用VAR就無法衡量此時的市場風險。

盡管VaR存在一定的缺陷，但這并不防礙它成為衡量市場風險的一個極為有價值的統計技術方法，VaR一經產生即以其對風險衡量的科學、準確、實用和綜合的特點受到包括監管部門在內的國際金融界的普遍關注，迅速發展成為風險管理的一種標準。VaR及其指標變量，幾乎被每一個主要的衍生金融工具交易商和越來越多的投資者及最終用戶所廣泛應用。

[1]周大慶等.風險管理前沿——風險價值理論與應用[M].北京：中國人民大學出版社，2004.

[2]宋逢明.金融工程原理－無套利均衡分析[M].北京：清華大學出版社，1999.

[3]John F.Marshall，Vipul Bansal.金融工程[M].宋逢明等譯.北京：清華大學出版社，2005.

[4]Cormac Butler風險值概論[M].于研等譯.上海：上海財經大學出版社，2002.

[5]Cormac Butler.風險值概論[M].于研等譯.上海：上海財經大學出版社，2002.