聯合卡諾圖在時序邏輯電路設計中的應用

盧容德 （長江大學電子信息學院，湖北 荊州434023）

時序邏輯電路經典的設計方法——驅動表法，是在完成狀態編碼的工作后，根據編碼后的狀態轉換圖和選擇的觸發器類型，列出對應的驅動表，再根據驅動表寫出驅動函數和輸出函數的卡諾圖，用卡諾圖化簡法得出最簡的驅動函數和輸出函數表達式，得出設計電路。然后根據電路中各觸發器的次態方程，用計算法求出電路無效狀態的次態，檢查電路是否具有自啟動功能。如果電路不能自啟動，還要適當修改設計，最后完成電路的設計任務[1-3]。這種方法在驅動函數的確定和自啟動功能的檢驗等方面，使用起來都顯得比較繁瑣。采用次態卡諾圖法，直接根據分離的次態卡諾圖得出最簡的次態函數，再根據次態方程確定驅動函數，可以使確定驅動函數的過程簡化，但仍然不能改善自啟動功能檢驗的不足[4-5]。為此，筆者直接根據次態聯合卡諾圖確定次態函數，提出了異步時序邏輯電路設計的驅動函數法和翻轉模式法，并舉例說明次態聯合卡諾圖在同步和異步時序邏輯電路設計中的應用。

1 同步時序電路的設計

1.1 設計方法

聯合卡諾圖設計法與經典的設計步驟完全相同，其不同點是直接根據次態聯合卡諾圖確定最簡次態函數。文獻[6]指出，時序邏輯電路的次態聯合卡諾圖，既是1個二維的狀態轉換表，又是1個表格式的狀態轉換圖。所以，按照經典的設計方法，只要完成了狀態編碼的工作，就可以直接得出次態聯合卡諾圖。所以，采用次態聯合卡諾圖的同步時序邏輯電路的設計步驟為：①邏輯抽象，得出描述對象過程的原始狀態轉換圖；②狀態化簡；③狀態賦值，也叫狀態編碼；④作出次態聯合卡諾圖；⑤確定觸發器，直接用次態聯合卡諾圖得出最簡次態函數，在化簡的過程中同時考慮自啟動的問題；⑥將次態函數與觸發器的特性方程相比較，確定各觸發器的驅動函數；⑦根據輸出要求確定輸出函數；⑧畫出邏輯電路。

1.2 設計舉例

以文獻[4]討論的例題為對象，說明聯合卡諾圖在同步時序邏輯電路設計中的應用，設計1個帶有進位輸出的同步13進制加法計數器，要求電路具有自啟動功能。

本例為計數器的設計，故直接進入同步時序邏輯電路的設計步驟③。按照8421碼編碼，得出13進制加法計數器的狀態轉換圖，如圖1所示。圖1中，C為進位信號。

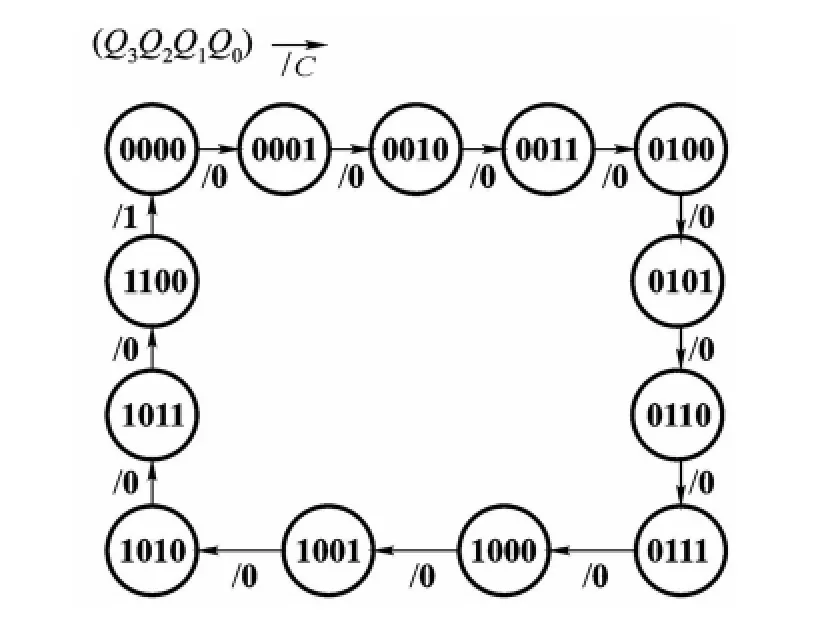
圖1 13進制加法計數器狀態轉換圖

根據狀態轉換圖，可以得出13進制加法計數器的次態聯合卡諾圖，如圖2（a）所示。為了使卡諾圖清晰可辨，圖2中沒有標出輸出函數。如果對8421碼加法計數器的狀態編碼比較熟悉，可以不用狀態轉換圖，直接寫出次態聯合卡諾圖。

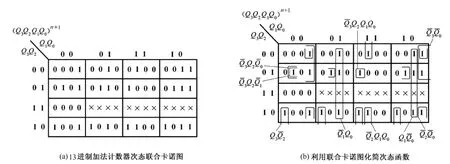
圖2 例1的次態聯合卡諾圖

選用JK觸發器實現電路的功能時，根據圖2（b）中的卡諾圈，確定最簡次態函數如下：

畫卡諾圈時，不能將次態函數對應的現態變量消去。如化簡Q3的次態函數時，不得利用無關項m15。根據卡諾圖中無關項圈了為1，不圈為0的規則，很容易判別該設計是否具有自啟動功能。根據圖2（b），無效狀態1101、1110、1111的次態分別為0010、0010、0000，電路能自啟動，故可以根據上述次態方程確定驅動函數。

根據狀態轉換圖不難得出進位信號表達式（即輸出函數）：

由此得到滿足設計要求的8421碼同步13進制加法計數器邏輯電路，如圖3所示。文獻[6]將已經作出的聯合卡諾圖拆開，再用卡諾圖法求出最簡次態函數表達式。檢驗自啟動功能時，將無效狀態對應的編碼代入次態函數表達式中計算次態，每個無效狀態要計算4次，而根據聯合卡諾圖檢驗自啟動，無需計算，因為次態聯合卡諾圖完整地描述了現態與次態的轉換關系。

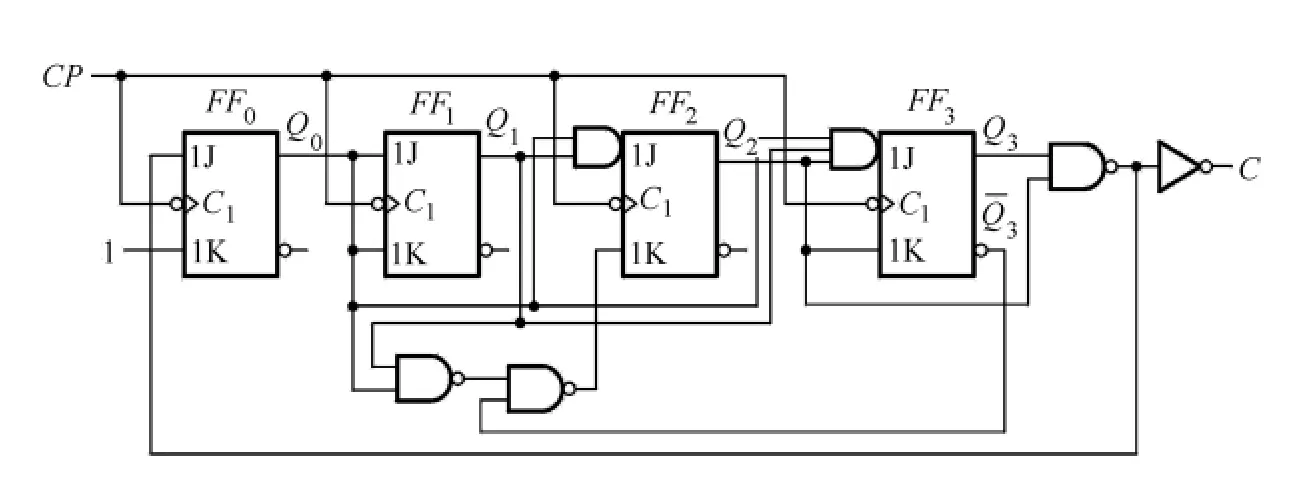
圖3 同步13進制加法計數器邏輯電路圖

2 異步時序電路的設計

2.1 設計方法

異步時序邏輯電路的聯合卡諾圖設計法與同步時序電路基本相同，其不同點在于觸發器時鐘信號的確定及由此產生的次態方程描述方式的變化。

與同步時序邏輯電路相比，異步時序邏輯電路的設計比較困難，但實現同一個邏輯功能，異步型時序電路比較簡單。采用次態聯合卡諾圖進行異步時序邏輯電路設計，其過程十分簡捷。

描述異步時序邏輯電路的次態方程為：

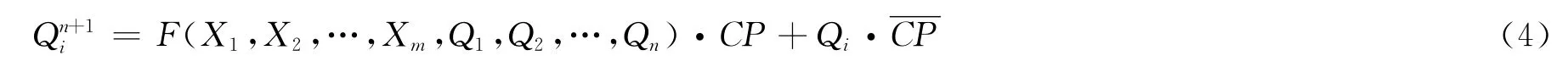
式中，Xj（j＝1，2，…，m）表示輸入信號；Qi（i＝1，2，…，n）表示第i個觸發器的現態表示第i個觸發器的次態。

式（4）揭示了如下2個基本關系：①無CP時（CP＝0），觸發器的次態保持原來的狀態不變。②有CP時（CP＝1），觸發器的次態由電路的輸入信號和現態的組合以及觸發器的特性方程決定。因而上述次態方程是異步時序邏輯電路聯合卡諾圖設計法的理論基礎。

設計異步時序邏輯電路的方法包括驅動函數法和翻轉模式法。

驅動函數法的要點是在完成狀態編碼工作后，首先作出次態聯合卡諾圖，再確定各觸發器的時鐘脈沖，然后寫出卡諾圖中時鐘有效區內電路的次態函數，最后將次態函數與觸發器的特性方程相比較，得出驅動函數的表達式，在時鐘有效區內，該方法與同步電路設計過程相同。

翻轉模式法的要點是在作出次態聯合卡諾圖后，首先圈出各次態的變化區（即翻轉區），再確定滿足驅動各觸發器的時鐘脈沖。按該種方法設計，觸發器工作在“翻轉”（即計數）方式，故驅動電路簡單。

驅動函數法是先確定CP，然后求驅動函數，而翻轉模式法是先確定驅動函數（即按照翻轉模式驅動），然后求CP。

例如，在圖4（a）所示的次態聯合卡諾圖中，Q0的負跳區完全覆蓋Q2的變化區，在Q0的負跳區外，Q2的次態不變。如果采用驅動函數法，則Q2可以選擇負邊沿觸發的觸發器，將Q0作為Q2的CP；如果采用翻轉模式法，則只需在Q2的翻轉區選擇CP。下面用負邊沿觸發的JK觸發器來加以說明。

采用驅動函數法時，取CP2＝Q0，Q2次態函數的卡諾圈如圖4（b）所示。在畫卡諾圈時，要注意以下2點：①在CP有效區內見“1”必圈；②在CP有效區外，所有最小項都是無關項，只要化簡需要，見 “0”也可以圈。

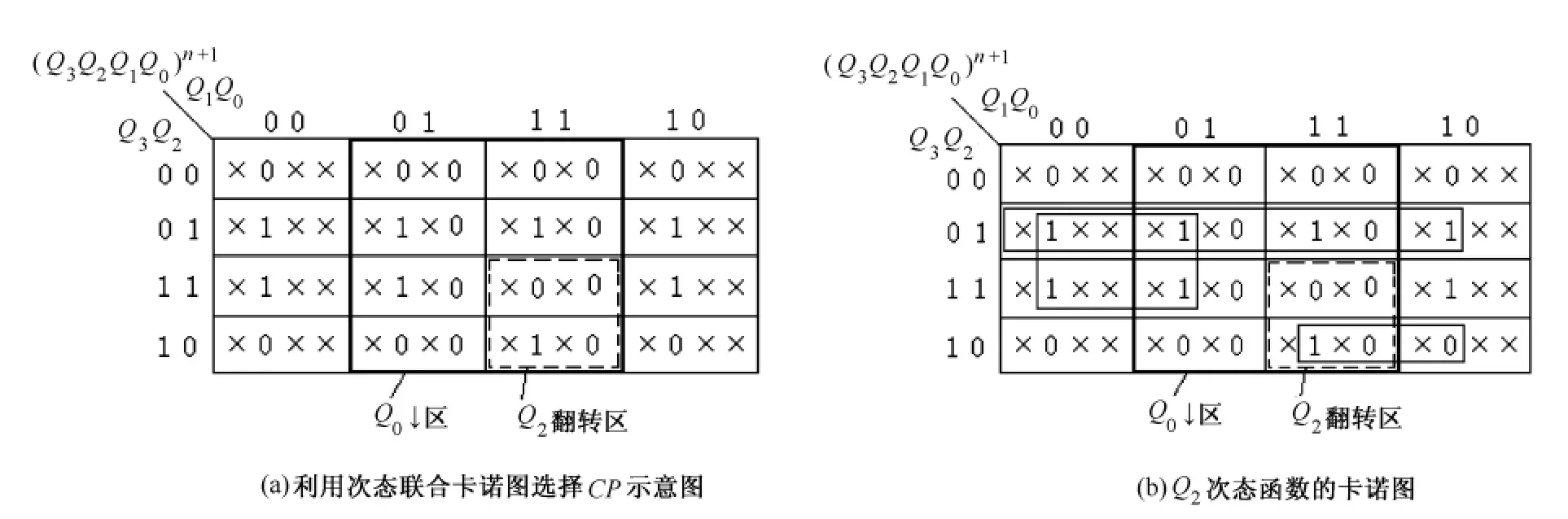
圖4 次態聯合卡諾圖在異步時序電路設計中應用

按驅動函數法得出的Q2的次態方程如下：

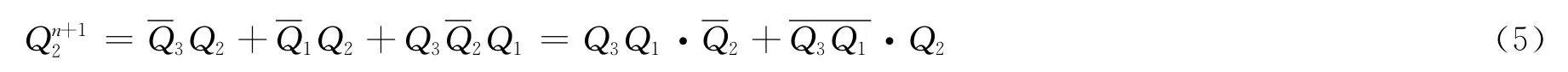
其驅動方程為：

按翻轉模式法得出Q2的時鐘方程如下：

其驅動方程為：

翻轉模式法實際上就是CP“使能”法，即讓覆蓋范圍較大的CP僅僅在觸發器的翻轉區起作用，此處就是讓Q0↓ 在∑m（11，15）有效。

觀察JK觸發器的內部電路發現，上述2種方法設計的驅動電路完全相同，這是因為JK觸發器的JK信號與CP信號就是邏輯與的關系。

異步時序邏輯電路設計中，選擇CP的原則如下：①翻轉最頻繁的觸發器用外接CP驅動，對于計數器，該觸發器是電路的最低位。②高位觸發器的CP由低位觸發器提供，低位觸發器提供的CP稱為內部時鐘脈沖。③當低位觸發器不能滿足高位觸發器CP的要求時，則該高位觸發器由外接CP驅動。④直接由外接CP驅動的觸發器，其驅動函數確定的方法與同步時序邏輯電路的方法相同。⑤當內部時鐘脈沖恰好覆蓋高位觸發器的翻轉區時，則該觸發器接成翻轉模式即可。⑥當內部時鐘脈沖覆蓋的范圍大于高位觸發器的翻轉區時，則該觸發器的驅動設計有驅動函數法和翻轉模式法。⑦內部時鐘脈沖的選擇，可以直接在次態聯合卡諾圖中用觀察法確定；也可以用波形圖 （時序圖）進行輔助分析[4]。

2.2 設計舉例

具體要求是設計1個具有自啟動功能的8421碼異步十進制減法計數器。

按照8421碼編碼后，十進制減法計數器的狀態轉換圖如圖5所示，圖中，B為借位信號。其次態聯合卡諾圖如圖6所示。

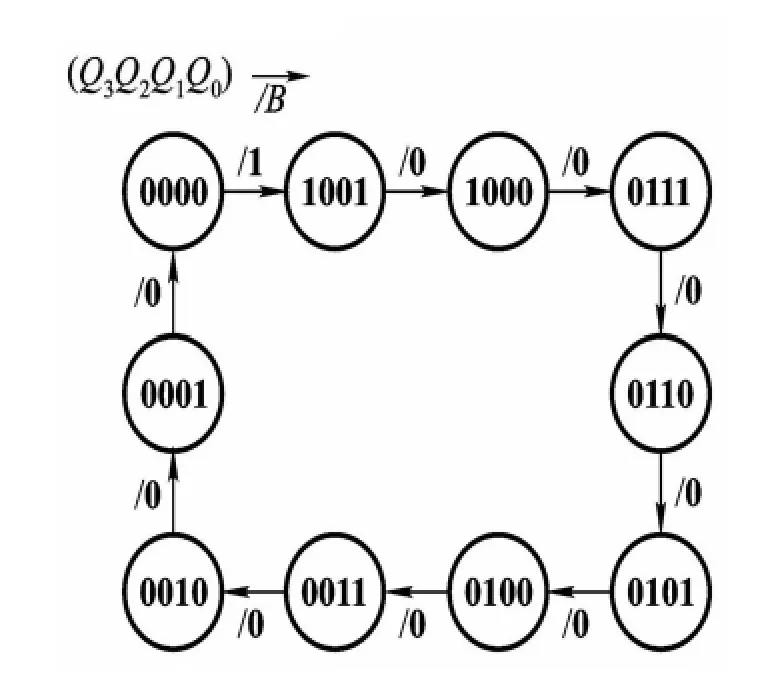
圖5 例2的狀態轉換圖

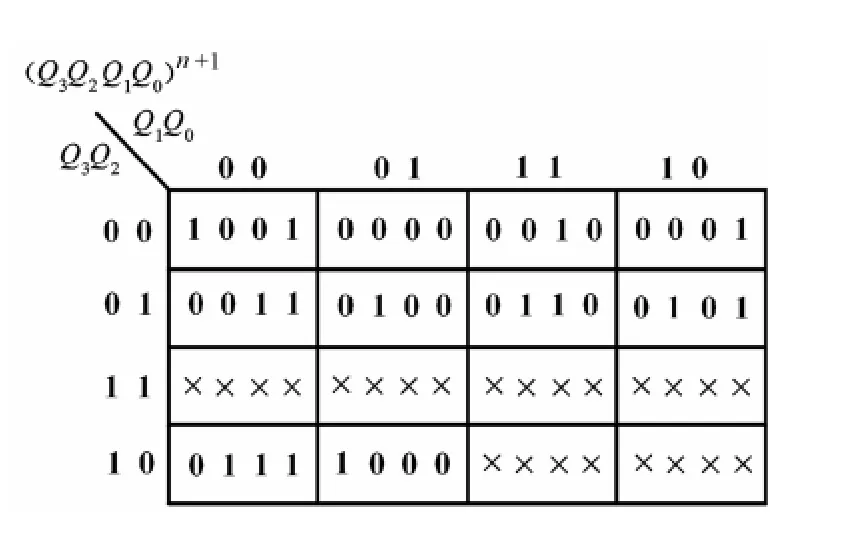
圖6 例2的次態聯合卡諾圖

選用負邊沿觸發的JK觸發器。首先，確定外接CP直接驅動觸發器FF0，直接利用聯合卡諾化簡Q0的次態函數。化簡時考慮到無關項，不難得出：

由于Q0工作在翻轉模式，故有：

故觸發器FF1驅動方程為：

接著，標出Q1的負跳區，如圖7（b）所示。按照Q2在Q1的負跳區內翻轉、在Q1的負跳區外保持的原則，標出Q2無效狀態的邏輯值，如圖7（b）所示。不難發現的負跳區恰好覆蓋Q2的翻轉區，故可以作為觸發器FF2的時鐘脈沖并且FF2工作在翻轉模式，因此有：

這里，化簡時利用了無關項m1。

FF3的驅動方程為：

根據狀態轉換圖得出借位信號表達式（即輸出函數）：

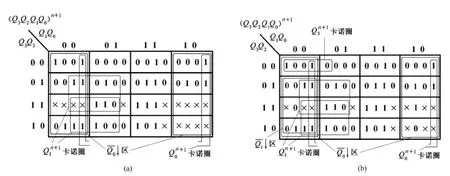
圖7 利用次態聯合卡諾圖的設計過程

最后，得到滿足設計要求的8421碼異步10進制減法計數器邏輯電路，如圖8所示。

根據圖7（b）所示的次態聯合卡諾圖及卡諾圈，考慮的無關項的邏輯值被圈為1、未圈為0，很容易驗證電路的自啟動性能。完整的狀態轉換圖如圖9所示。

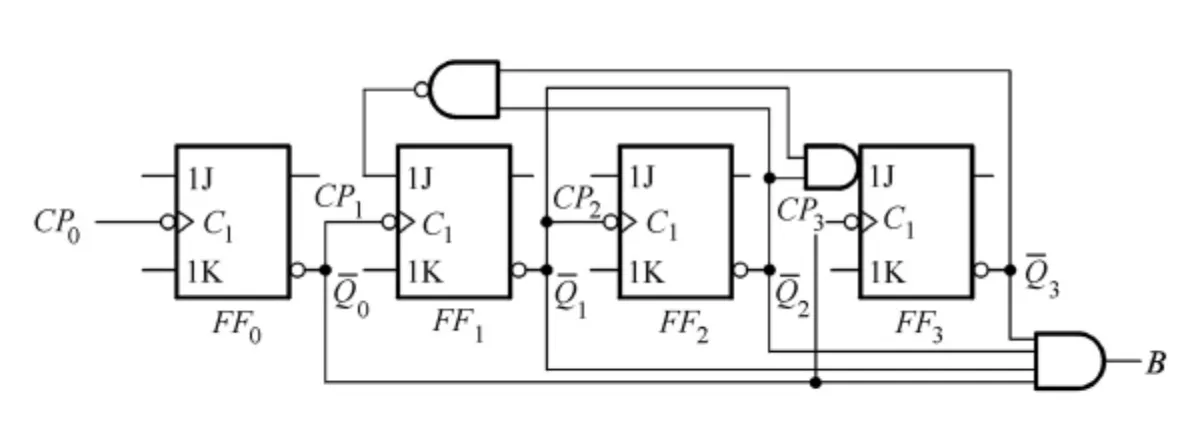
圖8 8421碼異步10進制減法計數器邏輯電路

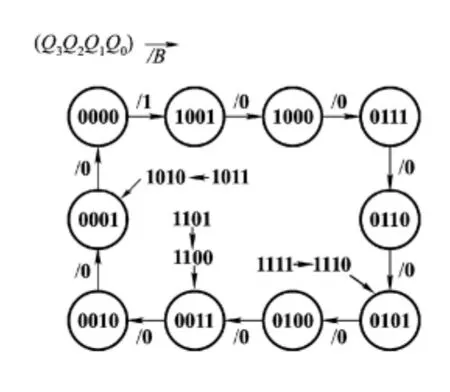
圖9 完整的狀態轉換圖

3 結 語

設計時序電路的關鍵是如何確定觸發器的驅動函數，使用次態聯合卡諾圖可以使確定驅動函數的過程簡化，而驅動函數法和翻轉模式法為時序電路設計的難點，它們為異步時序電路的設計提供了簡便有效的方法。對于時序電路自啟動功能的檢查，無論涉及到同步時序電路還是異步時序電路，次態聯合卡諾圖法都具有其獨特優勢。

[1]蔣立平.數字邏輯電路與系統設計[M].北京：電子工業出版社，2008.

[2]曹漢房.數字電路與邏輯設計[M].武漢：華中科技大學出版社，2004.

[3]歐陽星明.數字電路邏輯設計[M].北京：人民郵電出版社，2011.

[4]閻石.數字電子技術基礎[M].北京：高等教育出版社，2006.

[5]任駿原.基于次態卡諾圖的J、K激勵函數最小化方法及時序邏輯電路自啟動設計[J].浙江大學學報 （理學版），2010，37（4）：425-427.

[6]盧容德.聯合卡諾圖在邏輯電路分析中的應用[J].長江大學學報 （自然科學版 ），2009，6（4）：N61-65.