非均勻正交各向異性端頭帽熱應力分析①

程興華，李建林，楊 濤，李 理

(國防科技大學航天與材料工程學院，長沙 410073)

0 引言

高超聲速飛行器在出入大氣層或持續在大氣內飛行時，將承受巨大的氣動力和氣動熱。氣動熱載荷表現為表面與大氣的摩擦而達到較高的溫度，尤其是飛行器頭錐、翼前緣等部位。氣動熱不僅使材料的力學性能降低，而且在結構中產生熱應力，從而使變形加劇，高溫熱載荷引起的熱應力不容忽視。以往對高溫區的溫度、熱應力分析多為非線性、正交各向異性，而對復合材料因編織方法引起的物性非均勻性分析很少[1－5]。

本文以正交各向異性復合材料端頭帽為對象，研究非均勻材料物性引起的應力分布變化。

1 計算模型

1.1 熱彈性本構方程

在彈性力學中，應力和應變關系由廣義胡克定律確定。胡克定律是固體彈性材料在均勻常值溫度下的本構方程，如考慮溫度變化的影響，而不考慮溫度與變形之間的耦合關系，則材料的本構方程[6]可記為

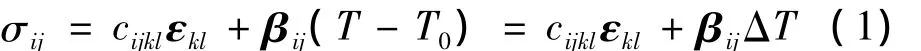
式中cijkl為彈性模量，也稱剛度系數;εkl為應變張量;βij是在應變為零時測得的熱模量，是一個對稱張量;T為當前溫度;T0為參考溫度，即cijkl測定時的溫度。

式(1)中的溫度變化ΔT一般用符號Θ來表示，這樣式(1)即可寫作:

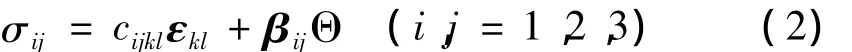
式(2)稱為杜哈梅爾-牛曼(Duhamel-Neumann)關系式。

1.2 瞬態傳熱本構方程

熱彈性理論離不開對傳熱規律的了解，傳熱有傳導、輻射和對流3種形式。其基本的能量守恒方程為

式中V為固體材料的體積;S為表面積;ρ為材料密度;U·為內能的時間變化速率;q為單位表面積上流入控制體的熱流率;r為單位體積內的其他熱增量。

假設U=U(T)，T為材料的溫度，q和r與材料的應力和位移無關。除相變產生的潛熱外，傳熱分析的本構方程為

其中，c(T)為材料的比熱容，當給定潛熱時，認為它是比熱容的一個附加量。多數情況下，認為相變在一定的溫度范圍內發生是合理的。

導熱遵守傅里葉定律:

式中 λi為熱導率。

物體中的溫度分布，無論是定常還是非定常，都需要給定邊界條件[7－8]，對于非定常情況還須給出時間的初始條件，這才能求解方程(3)內的溫度分布。

2 數值方法

2.1 順序耦合算法

持續受熱的特征決定了飛行器在某一時刻的受熱情況不僅與這一時刻的飛行條件有關，還與這之前飛行器自身熱環境所經歷的時間歷程緊密相關。在以往氣動加熱分析中，多數研究的是瞬態情況，即在一定的飛行(來流)條件和外表面壁溫條件下給出外表面的熱流分布。這種瞬態結果尚不足以用來判斷飛行器在持續受熱過程中的各種中間狀態，因為在各個中間狀態對應的物體自身熱環境都是經歷了一定時間歷程后形成的，考慮各傳熱環節之間的耦合性十分必要。

順序耦合算法又稱松耦合方法，其特點是流場與結構計算域在接觸面上周期性交換數據，主要體現為流體與結構接觸面上的邊界條件處理。

本文通過Fortran用戶子程序對大型非線性有限元計算軟件Abaqus進行二次開發。每個時間增量步開始時，用戶子程序讀取端頭帽外表面上的溫度，將計算得到的氣動熱流傳遞給Abaqus主程序;Abaqus主程序根據邊界熱流進行熱應力計算;如此順序耦合循環，直至彈道結束點，最終完成端頭帽熱應力分析。

2.2 物理數學模型

端頭帽為球錐結構，如圖1所示，球頭半徑為RN，錐身半錐角θ，總長L。由對稱性，考慮計算工況含有攻角、材料的正交各向異性，數學模型取周向180°。xy平面為端頭帽對稱面，α為攻角，αg為子午面與xy平面的夾角。

網格劃分如圖2所示。由于頭部熱流梯度比較大，對頭部網格進行了適當加密。網格單元選取耦合溫度——位移單元C3D8T和C3D6T。

圖1 模型三維視圖Fig.1 3D view of them odel

圖2 網格劃分Fig.2 M esh for discretization

2.3 材料模型

端頭帽材料以周向0°、90°正交編織，材料沿端頭帽軸向性能一致。由于x、z方向(與端頭帽軸線垂直的平面)交錯疊加，消除了x、z方向性能差別，但不能消除xz平面內45°方向的性能差異，即材料性能在xz平面內呈現非均勻性。根據測試結果，在45°方向主要是力學性能(彈性模量E)的差異，熱物理性能(表1)差異很小，在本文研究中可忽略。

根據以往雙向拉伸性能試驗，可判斷在與炭布x向或z向的夾角為45°時，材料的模量和強度減小到x向或z向的70%。

端頭帽材料模型如圖3所示。材料力學性能在xz平面內繞y軸以90°周期分布。在第Ⅰ象限內，以材料在x方向的力學性能為標準(100%);當0°＜αg＜45°時，材料力學性能隨αg增大而減小;至αg=45°時，力學性能減小至x方向的70%;當45°＜αg＜90°時，材料力學性能隨αg增大而增大;至αg=90°時，力學性能增大至100%，與x方向性能一致。本文采用線性插值方法獲取αg在不同角度時的端頭帽力學性能。端頭帽在主軸方向的力學性能如表2所示。

2.4 初邊值條件

端頭帽彈道曲線如圖4所示。設端頭帽初始溫度均勻分布，取300 K，計算總時間為977 s。

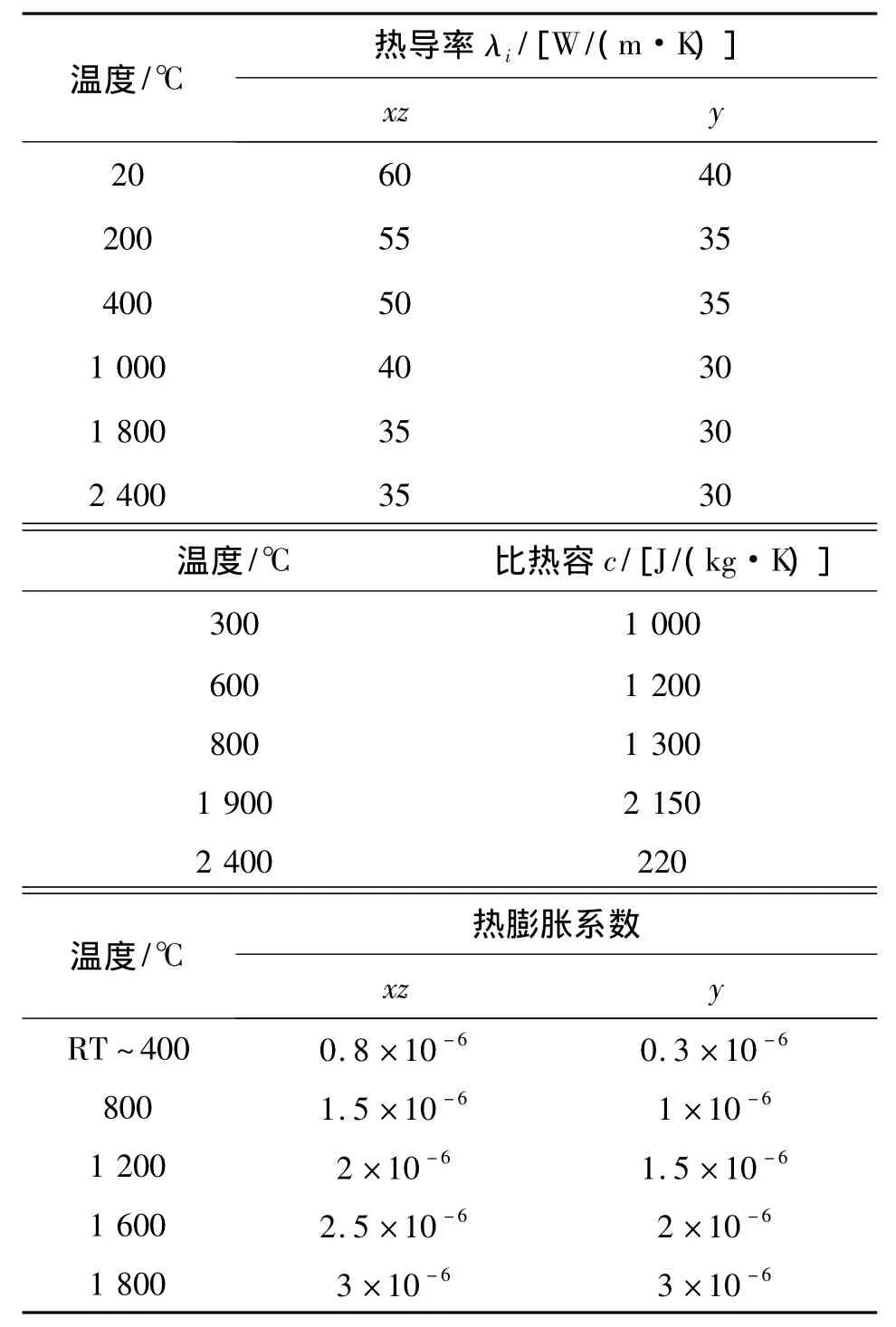
表1 端頭帽材料熱物理性能Table 1 Thermal physical properties of the nosecap material

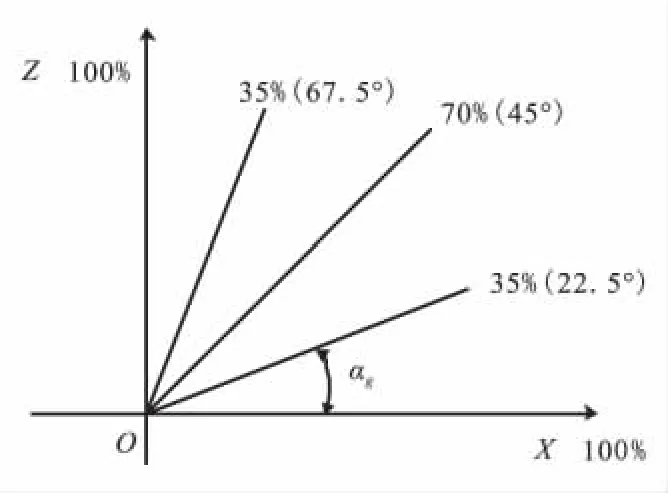
圖3 力學性能插值示意圖Fig.3 Interpolation sketch for mechanics properties

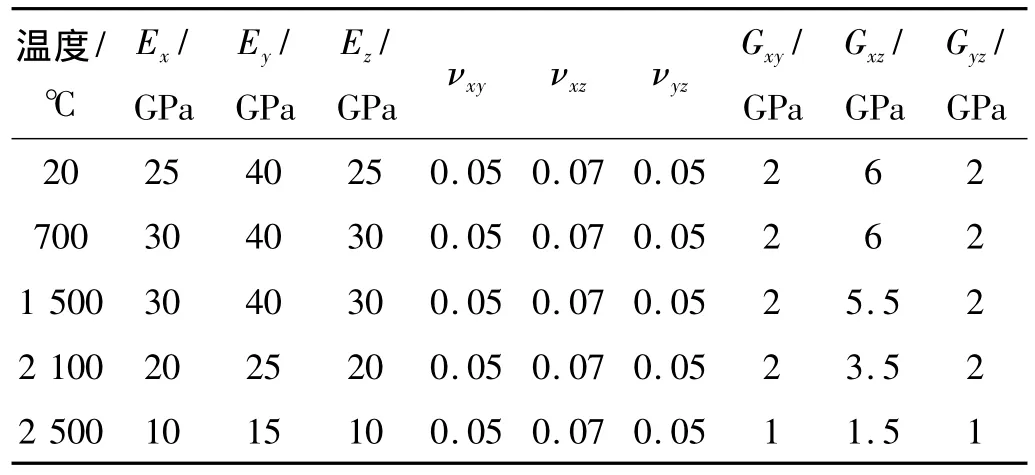
表2 端頭帽材料力學性能Table 2 M echanics properties of the nosecap material

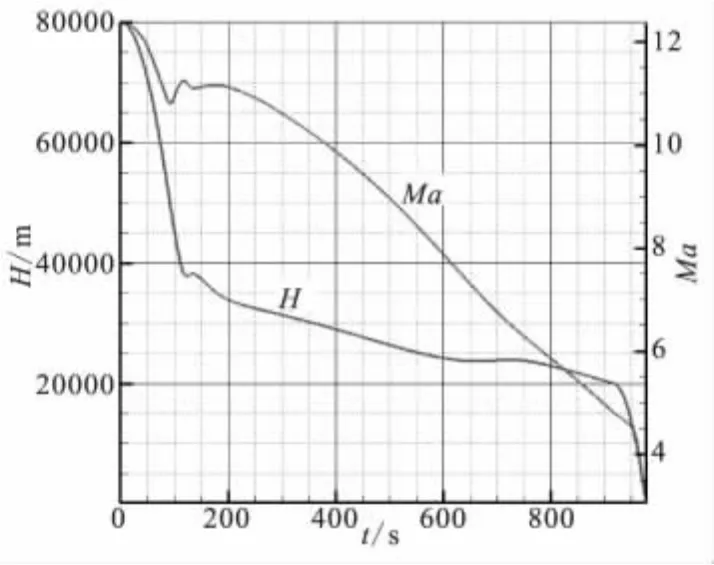
圖4 端頭帽彈道曲線Fig.4 Flight trajectory of the nosecap

彈頭在大氣環境下高速飛行，不僅受氣動力作用，還受氣動加熱作用。端頭帽的邊界條件有熱邊界、氣動壓力邊界、對稱邊界、連接支撐邊界。

(1)熱邊界為端頭帽外表面，受氣動加熱作用，同時向外部環境空間輻射熱量。

本文采用Lees模型[9]計算氣動加熱熱流通量:

式中Q為進入表面的熱量;S為邊界表面;t為時間;ψ(x，y，z，t)為給定的熱流通量函數。

端頭帽為熱結構，表面輻射到環境空間的熱力密度為

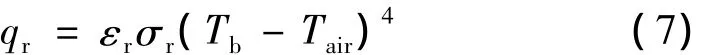
式中 εr為端頭帽表面熱輻射率，一般假設εr=0.8;σr為波爾茲曼常數，σr=5.67×10－8;Tb為端頭帽的表面溫度;Tair為環境大氣溫度。

(2)氣動壓力邊界同樣作用在端頭帽的外表面，壓力值由已知條件給出。

(3)對稱邊界為端頭帽縱對稱面，在對稱面上:

式中U3為z方向的位移;UR1為繞x軸的旋轉;UR2為繞y軸的旋轉。

(4)連接支撐邊界為端頭帽尾部，與彈體連接，假設連接支撐邊界為固支。

3 結果分析

3.1 溫度分布

表面節點溫度變化主要受氣動加熱和熱輻射影響，當氣動加熱與熱輻射平衡時，節點溫度達到極大值。圖5為0°攻角母線溫度變化曲線，可見駐點附近溫差較小，駐點最高溫度為2 356 K;在彈道前段，表面溫度在球頭沿母線急劇下降，而在錐身下降緩慢;在彈道末段，由于高溫的強輻射作用，端頭帽球頭溫度較錐身下降快;977 s時球頭溫度低于錐身溫度，端頭帽最低溫度在駐點(約1 001 K)，最高溫度在尾部軸線上(約1 049 K)。由此可見，在彈道末段，端頭帽內部溫度較高，表面熱輻射大于氣動加熱，端頭帽向外放熱。

圖6為0°攻角典型時刻的溫度云圖。由于熱導率較小，在870 s以前，高溫區主要集中在端頭帽球頭，溫度梯度較大，而在錐身部溫度分布較為均勻、梯度較小。在870 s后，高溫區向錐身擴展，但此時最高溫度已小于1 200 K，最大溫差小于50 K，整體分布較均勻，溫度梯度較小。另外，由于輻射換熱與表面溫度的四次方成正比，在260 s以前，輻射換熱小于氣動加熱，駐點溫度急劇升高;之后，輻射換熱大于氣動加熱，駐點溫度逐漸減小，駐點位置由向內加熱轉為向外放熱。

圖5 0°攻角母線溫度變化Fig.5 Temperature profile along generating line under 0°angle of attack

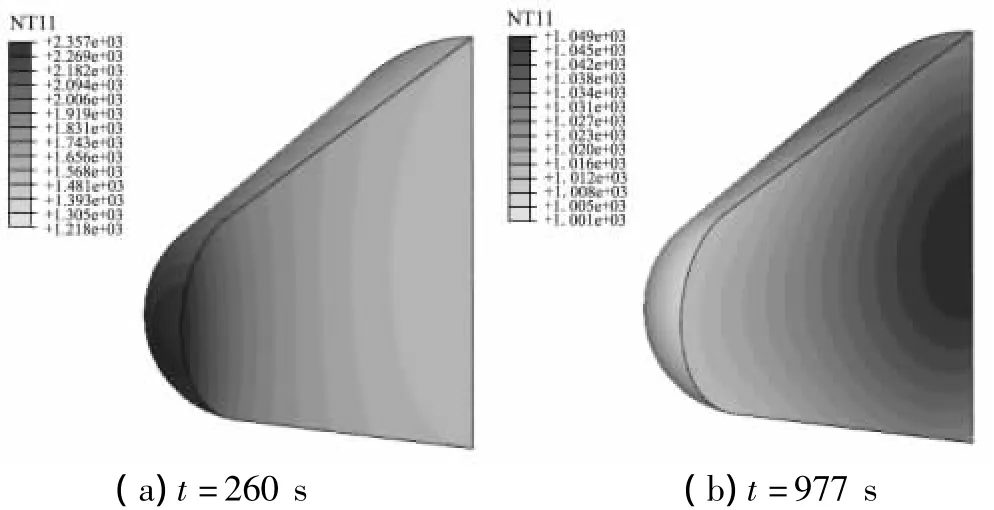
圖6 0°攻角溫度云圖Fig.6 Temperature distributions under 0°angle of attack

3.2 應變-應力分布

在復合材料的強度準則中以最大應變準則和最大應力準則、蔡-希爾準則、蔡-吳準則[10]應用的較多。Mises等效應力可以看作蔡-吳準則的一個特例，其定義為

其中，S為偏應力張量，S=σ+p I(σ為應力，I為單位矩陣，p=－σii/3為等效壓應力，也就是常見的p=(σx+σy+σz)/3)。因此，以下重點對端頭帽的應變和Mises等效應力進行分析。

圖7為0°攻角典型時刻主彈性應變云圖，圖8為0°攻角典型時刻x向熱應變云圖。由圖7、圖8可知，彈道初段，由于端頭帽頭部高溫區集中，局部大熱膨脹拉伸頭部，使得頭部出現環形大彈性應變區域;彈性應變較熱應變為小量，總應變分布與熱應變分布相同，大小基本相當。在彈道中段、末段，高溫區向后移動，端頭帽尾部固定端的彈性應變凸顯出來，總應變在端頭帽尾部以約束條件產生的彈性應變為主，而其余主體部分仍以熱應力為主。

圖7 0°攻角主彈性應變云圖Fig.7 Principal strains distributions under 0°angle of attack

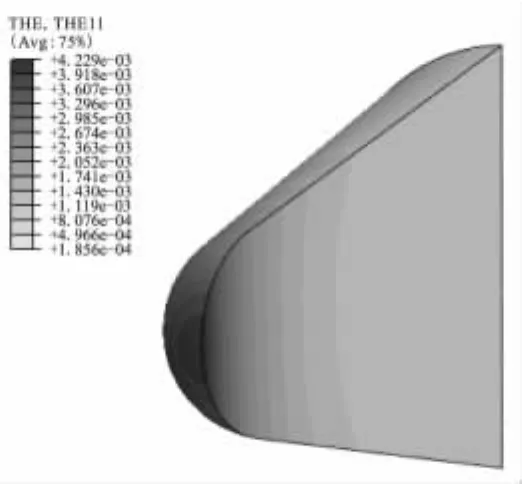
圖8 0°攻角x向熱應變云圖(t=120 s)Fig.8 x direction thermal strain distributions under 0°angle of attack(t=120 s)

圖9為0°攻角典型時刻Mises應力云圖。由圖9可知，在彈道初段，由于熱膨脹作用，端頭帽外表面形成環狀Mises應力分布，內部也存在較大應力;在彈道末段，熱應力較小，尾部由于固定約束而形成較大的應力。在熱應力集中段，外表面Mises應力最大;在尾部約束處，內部Mises應力最大。在垂直于y軸的剖面上，Mises應力分布以90°為周期(如圖9中的尾端面應力云圖)，在0°、90°方向最大，逐漸過渡到最小的45°方向。

3.3 攻角對溫度、應力的影響

受攻角影響，頭部駐點下移(最大溫度2 351 K)，低溫點上移，在尾部背風位置附近。高溫區域仍集中在頭部，由于頭部為球形，其以駐點為中心的分布趨勢與0°攻角時基本相同。圖10為10°攻角母線溫度分布曲線。由圖10可知，10°攻角時，迎風母線(αg=180°)溫度最高，側面水平母線(αg=90°)近似為迎風和背風母線(αg=0°)的平均值。

圖9 0°攻角M ises應力云圖Fig.9 M ises equivalent stress distributions under 0°angle of attack

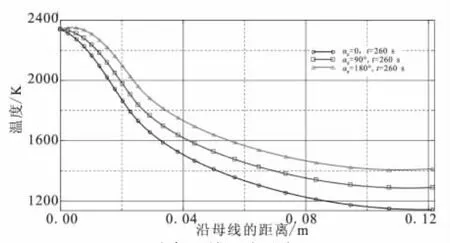
圖10 10°攻角母線溫度分布(t=260 s)Fig.10 Tem perature profile along generating line under 10°angle of attack(t=260 s)

圖11為10°攻角x向熱應變云圖。由圖11可見，除約束端外，10°攻角端頭帽總應變在彈道初段仍以熱應變為主。熱應變集中在球頭部，以攻角α=10°的球頭徑向對稱分布;總應變最大值在駐點附近;主彈性應變在迎風面較大，高彈性應變區域在迎風面較寬。

對應于應變分布，彈道初段Mises應力在迎風面上出現極大值，且呈現較寬區域的應力集中(圖12)。彈道末段，10°攻角Mises應力軸向分布與無攻角時基本相同:熱應力較小，尾部由于固定約束而形成較大的應力。受攻角和材料性能參數的雙重影響，在垂直于y軸的剖面上，Mises應力在αg=180°子午面內最大，αg=45°子午面內最小(圖13)，這種現象在彈道初段最為明顯。分析可知，最大Mises應力為111 MPa，較無攻角時(104 MPa)略大。

圖11 10°攻角x向熱應變云圖(t=260 s)Fig.11 x direction thermal strains distributions under 10°angle of attack(t=260 s)

圖12 10°攻角M ises應力云圖(t=110 s)Fig.12 M ises equivalent stress distributions under 10°angle of attack(t=110 s)

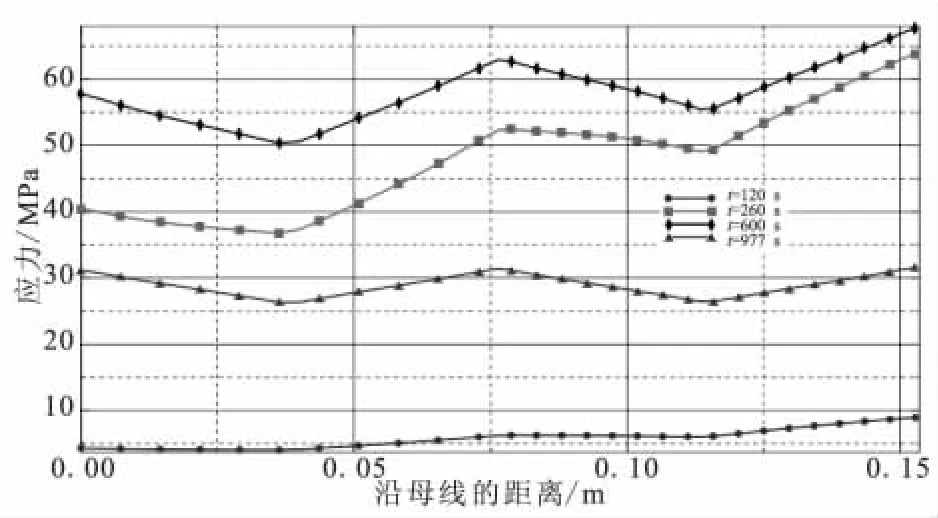
圖13 10°攻角尾部外表面周向M ises應力分布Fig.13 Circum ferential M ises stress distributions on tail surface under 10°angle of attack

在端頭帽結構設計時，應將材料的xz平面45°方向設置在迎風線上。這樣可減小端頭帽應力極值，使端頭帽周向應力分布趨于均勻，有利于端頭帽與彈體連接。

4 結論

(1)彈道初段，表面熱輻射小于氣動加熱，端頭帽溫度迅速升高;彈道末段，端頭帽內部溫度較高，表面熱輻射大于氣動加熱，端頭帽向外放熱。有攻角時，側面水平母線溫度近似為迎風和背風母線平均值。

(2)彈道初段，局部大熱膨脹拉伸頭部，在頭部形成環狀彈性應變區。在彈道中、末段，高溫區向后移動，總應變在端頭帽尾部以固定約束條件產生的彈性應變為主，而其余主體部分仍以熱應力為主。因此，端頭帽尾端的連接方式十分重要。

(3)在垂直于端頭帽y軸的剖面上，Mises應力分布以90°為周期，在0°、90°方向最大，逐漸過渡到較小的45°方向。

(4)受攻角影響，Mises應力在迎風子午面內最大，水平子午面內最小，這種現象在彈道初段最為明顯。在端頭帽結構設計時，應將材料的xz平面45°方向設置在迎風線上。

[1] Grant Palmer.A heating analysis of the nosecap and leading edges of the X-34 vehicle[R].AIAA 98-0878.

[2] 尹蓮花，劉莉，張帥.燒蝕材料的近程高速彈頭熱應力數值仿真研究[J].系統仿真學報，2008，20(15):3966-3968.

[3] 姜志杰，張擘毅，何浩.高超聲速飛行器鼻錐的熱環境和結構熱分析研究[J].導彈與航天運載技術，2009，(4):14-17.

[4] 易龍，孫秦，彭云.復合材料頭錐結構氣動熱應力分析方法研究[J].機械強度，2007，29(4):686-692.

[5] Rosario Borrellia，Aniello Riccio，Domenico Tescione.Thermo-structural behaviour of an UHTCmade nosecap of a reentry vehicle[J].Acta Astronautica，2009，65:442-456.

[6] 范緒箕.高速飛行器熱結構分析與應用[M].北京:國防工業出版社，2009.

[7] 朱濱.彈性力學[M].合肥:中國科學技術大學出版社，2008.

[8] 趙鎮南.傳熱學[M].北京:高等教育出版社，2002.

[9] 中國人民解放軍總裝備部軍事訓練教材編輯工作委員會.高超聲速氣動熱和熱防護[M].北京:國防工業出版社，2003.

[10] 王寶來，吳世平，梁軍.復合材料失效及其強度理論[J].失效分析與預防，2006，1(2):13-19.