NA樣本情形下雙參數指數分布族參數EB估計的漸近性討論
劉榮玄,范發明,吳高翔
(井岡山大學 數理學院,江西 吉安 343009)
0 引言
近幾十年來,已有許多文獻研究經驗Bayes統計推斷,這些研究文獻中絕大多數都是在獨立同分布的樣本下進行的。然而在滲透性理論和可靠性理論等實際問題中,所獲得的樣本常常不是獨立的,而是具有某種相關性,負相協(NA)和正相協(PA)樣本就是兩種常見的樣本.關于估計問題,在許多情況下正誤差(過高估計)和負誤差(過低估計)所造成的損失相差很大,因此許多研究經驗Bayes統計推斷的文獻采用了非對稱損失函數,LINEX損失就是其中常用的一種。雙參數指數分布應用很廣,一些產品的壽命分布都可以用它來刻畫,如汽車、飛機和水壩等壽命都服從這種分布。有關這些方面的研究有許多學者在不同的刊物上發表了文章,文獻[1]討論了在NA樣本情形下刻度指數族參數的經驗Bayes檢驗問題,文獻[2]討論了在NA樣本情形下單邊截斷型分布族位置參數的經驗Bayes估計,文獻[3]討論了在LINEX損失函數下單邊截斷型分布族參數的EB估計,文獻[4]討論了刻度指數族參數的經驗Bayes估計的收斂速度,文獻[5]討論了線性指數分布參數的經驗貝葉斯估計,文獻[6]討論了對稱熵損失下指數分布參數的估計,文獻[7]討論了定數截尾數據缺失場合下雙參數指數分布參數的貝葉斯估計。本文將在NA樣本情形下,假設LINEX損失函數,研究雙參數指數分布位置參數的EB估計,并證明所得到的估計是漸近最優的。
假設雙參數指數分布為

其中α為位置參數,或稱門限參數、保證時間參數,當α表示壽命、時間時,α自然是非負的;β>0為尺度參數。
為便于研究位置參數α的估計,不妨假設β為常數,于是對給定的α時,隨機變量(r.v.)X的條件密度函數為

這里的,Ω 為參數空間 α∈Ω=(0,+∞)。
設 α 的先驗分布為 H(α),屬于先驗分布族 F={H(α):E(eαβ-1)<∞,β>0},則 r.v.X 的邊緣分布為


取損失函數為如下的LINEX函數,即

其中θ(x)為參數α的判決函數,c≠0,c為實數,是損失函數的尺度參數,可根據雙參數指數分布的參數β的值確定c的取值,滿足βc>1。于是參數α的Bayes估計為


這里 E(x,α)表示對(X,α)的聯合分布取期望。
從上式可知,如果參數α的先驗分布是已知的,θ^BE(x)的Bayes 風險 R(θ^BE(x),H(α))可以計算出來,然而,通常 α 的先驗分布 H(α)是不知道,按(5)式得不到θ^BE(x)的 Bayes估計。 也無法得到它的Bayes風險,但考慮到人們過去所做的工作一般都有記載,因此,下文將借用歷史數據,采用概率密度核估計的辦法,構造一個形如(5)式的參數α的EB估計θ^BE(x),以此估計量來近似代替Bayes估計θ^BE(x),并且可以證明這種代替在LINEX損失下其風險可任意接近 R(θ^BE(x),H(α))。收斂速度為
1 EB估計的構造
假設(X1,α1),(X2,α2),…(Xn,αn),(X,α)為一串具有相同分布的隨機向量,X1,X2,…Xn,X,為同分布弱平穩NA隨機變量序列,它們是可觀測,有共同的邊緣概率密度 m(x);X1,X2,…Xn為歷史樣本,X為當前樣本,α1,α2,…αn和α為不可觀測的,但有相同的先驗分布 H(α)。 設 m(x)∈CS,M,x∈R1,其中 s≥2,為正整數,CS,M表示R1中的一族概率密度函數,其s階導數存在,連續其絕對值不超過M。對NA樣本序列的協方差結構假設為

下面利用歷史樣本和核函數定義m(x)的核估計。
設K(x)為Borel可測實值核函數,且滿足

K(x)為有界的,除有限點集外是可微的,且微分有界;
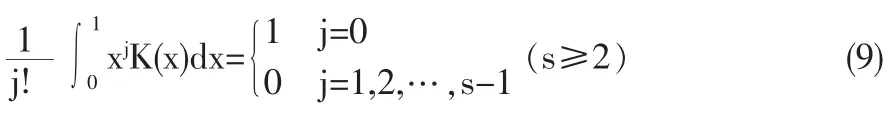
定義m(x)的核估計為

其中當n→∞時,hn→0,定義G(x)的估計為

令
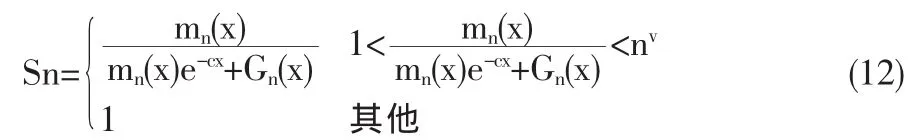
其中0<v<1,它的取值視實際情況而定,根據上述估計,再定義參數α的EB估計

它的全面Bayes風險為

其中 E*表示對(X1,X2,…Xn,X,α)的聯合分布求數學期望.以下證明這一EB估計的漸近性,說明在一定的條件下,用歷史數據估計參數α是有效性的。
2 漸近性的證明
在證明EB估計的漸近性之前先證幾個引理,并假設c1,c2,c3…為任意正常數,且在不同的地方可以代表不同的常數。
引理1 假設 a>0,b>0則有

證明:見文獻[8]引理1。
引理2 在LINEX損失函數下有

這里的 En 和 Ex 分別表示對隨機變量(X1,X2,…,Xn)和X的分布求數學期望。
證明:見文獻[8]引理2。
引理3 設Y,Y'分別為r.v,y,y'為實數,L>0,則對 0<γ<2有


證明:見文獻 [9]引理3.1。
引理4設r.vX和Y為NA的,都有有限的方差,則對任何可微函數g1和g2總有
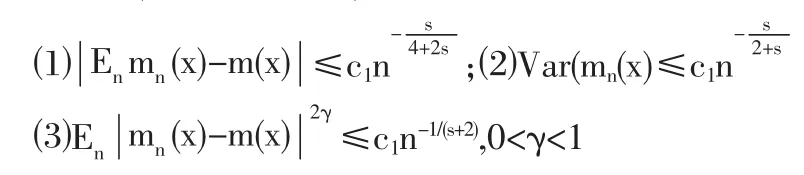
證明:見文獻[10]引理1。
引理5 X1,X2,…Xn,…,為同分布弱平穩的NA隨機變量序列,滿足條件(7)式,m(x)∈CS,M,m(x)由(10)式給出,則當hn=n-1/(2s+4)時(s>1,為自然數),有
⑴式的證明:因為

將m(x+hny)在x處展成s+1項Taylor級數,再由m(x)∈CS,M可得

⑵式的證明:由(10)有

由K(x)的有界性得到

由K(x)的定義及引理4可得

再由(7)式成立和的弱平穩性得到

于是有

⑶式的證明:由C-R不等式和Jensen不等式以及(20)、(25)式得

引理6設X1,X2…Xn,…,為同分布弱平穩的NA隨機變量序列,m(x)∈CS,M,βc>1,Gn(x)由(12)式給出,hn=n-1/(2s+4),則有

證明:由C-R不等式及Jensen不等式

由引理5得

所以

引理 7 如果 S(x)<∞ 則有 R(θ^BE(x),H(α))≤∞.
引理的結論很容易證明,證明(略)。
定理1設X1,X2,…Xn…,為同分布弱平穩的NA隨機變量序列,s>1為任意給定自然數,0<γ<1為任意實數,假設(7)式成立,并滿足下例條件
⑴m(x)∈CS,M;⑵βc>1;⑶E(eαβ-1)<∞
⑷Ex(S(x))η<∞,η>2

證明:根據引理1及引理2可得
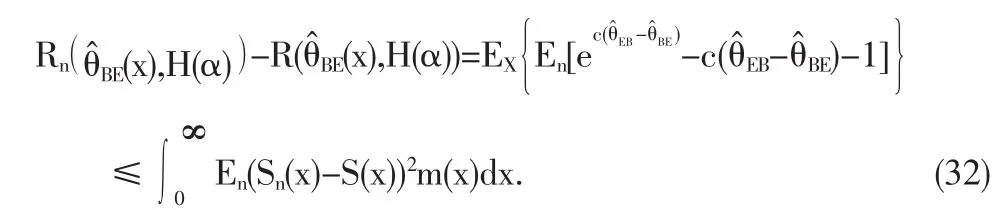
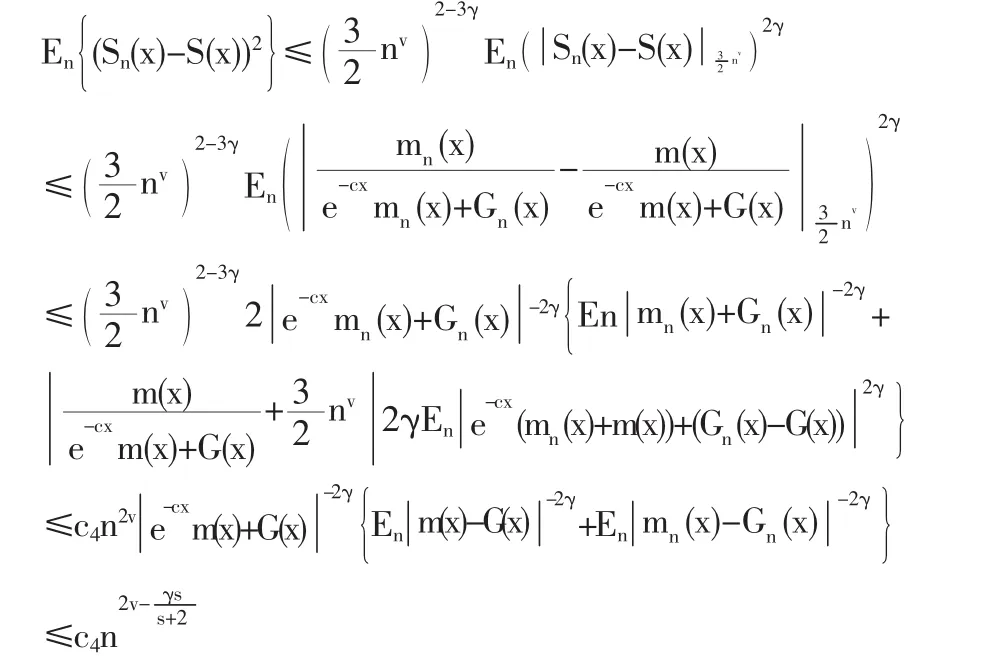
于是有
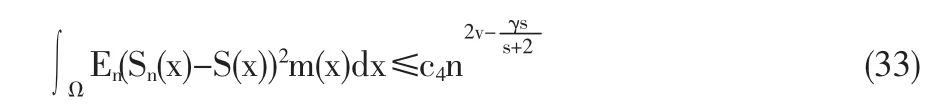
當x∈Ω時有

由H?lder不等式和Markov不等式有


從而有



顯然對于任意接近1的γ,只要定理中的條件成立,α的EB估計的收斂速度可任意接近于1[11]。
3 例子
下面的例子說明存在滿足定理條件的先驗分布。
如果參數α給定時,r.vX的條件概率密度由(2)式給出,設α 的先驗分布為 α~U[a,b],b>a>0,這時有
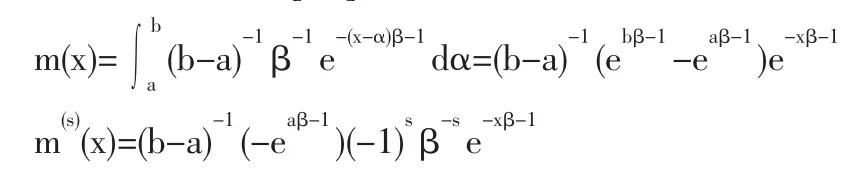
因此對于任意的大于1的正整數s,m(x)∈CS,M。又因為

則不難驗證定理中的條件全都成立。
[1]韋來生.刻度指數族參數的經驗貝葉斯檢驗問題:NA樣本情形[J].應用數學學報,2002,(3).
[2]許勇,師義民.NA樣本情形下單邊截斷型分布族位置參數的經驗Bayes估計[J].應用數學,2001,14(4).
[3]康會光,趙小山.Linex損失函數下單邊截斷型分布族參數的EB估計[J].應用數學,2001,14(3).
[4]王立春,韋來生.刻度指數族參數的經驗Bayes估計的收斂速度[J].數學年刊,2002,(5).
[5]陳家清,劉次華.線性指數分布參數的經驗貝葉斯估計[J].華中科技大學學報,2006,(10).
[6]孔令軍,宋立新.對稱熵損失下指數分布參數的估計[J].吉林大學自然科學學報,1998,(2).
[7]劉菡,劉次華.定數截尾數據缺失場合下雙參數指數分布參數貝葉斯估計[J].武漢大學學報(理科版),2006,52(3).
[8]劉榮玄,張波.指數族刻度參數EB估計的漸近最優性[J].數理統計與管理,2010,29(5).
[9]趙林城.一類離散分布參數的經驗貝葉斯估計的收斂速度[J].中國數學研究與評論,1981,(1).
[10]Wei,L.S.Convergence Rates of Empirical Bayes Estimation for a Rameterofone-sided Truncated Distribution[J].Annals of Math,1985,6A(2).
[11]陳希孺.高等數理統計[M].合肥:中國科學技術大學出版社,1999.
[12]Berger J O.統計決策論及Bayesr分析[M].賈乃光,吳喜之譯.北京:中國統計出版社,1998.

