應用組合預測法對我國月度PPI的預測評價
杜淑女,王斌會
(暨南大學 統計系,廣州 510632)
0 引言
PPI是衡量工業企業產品出廠價格變動趨勢和變動程度的指數,是反映某一時期生產領域價格變動情況的重要經濟指標,也是制定有關經濟政策和國民經濟核算的重要依據,而經濟指標的準確預測是國家對宏觀經濟正確調控的必要前提,但經濟系統是一個非常復雜的系統。因此要準確地預測某一趨勢,必須從多個方面進行考慮。每種預測各有其特點,在不同的方面有各自的優劣,因此為了準確地預測結果,可考慮采用組合預測法進行預測。對于同一預測問題而言,由于考慮的角度、方式和層次等不同,可為其提供不同的預測方法,將這些方法進行組合,可增大信息量,能夠更好地進行預測。組合預測將各種預測效果進行綜合考慮,比單個預測模型更系統、更全面。而且,Bates和 Granger證明了兩種或兩種以上無偏的單項預測可以組合出優于每個單項的預測結果,即能夠有效地提高預測的精度。為了有效地利用各種模型的信息,提高模型的預測精度與模擬評價效果,有必要對PPI進行組合預測。組合預測方法是建立在最大的利用信息的基礎上,它通過組合多個單項預測模型,集結這些模型中所包含的信息,因此,在大多數情況下,通過組合模型進行預測,更全面、更可靠,可以達到改善預測結果的目的。
基于組合預測模型的優越性和自回歸移動平均模型的建模機理,本文將以 2001年 1月至2010年 7月的月度定基 PPI數據為對象,建立了三個單項 ARIMA模型,為了有效地利用各種模型的信息,提高模型的預測精度與模擬評價效果,本文依據組合預測的原理將這三個單項預測模型進行組合,通過實例分析和精度檢驗。
1 組合預測理論
組合預測法是指通過建立一個組合預測模型,把多種預測方法所得到的預測結果進行綜合,以得到一個較窄的預測取值范圍供系統分析和決策使用。由于組合預測模型能夠較大限度地利用各種預測樣本信息,比單項預測模型考慮問題更系統、更全面,因而能夠有效地減少單個預測模型受隨機因素的影響,從而提高預測的精度和穩定性,下面分別具體介紹幾種組合預測法。
1.1 最優加權法
現在運用最廣泛的組合預測法是最優組合預測法,最優組合預測就是對單一預測方法進行組合得到最優權數,也叫最優加權法。最優加權法的基本原理是依據某種最優準則構造目標函數Q,本文中目標函數為殘差平方和即Q=eTe,在約束條件下運用最小二乘法極小化 Q求得綜合模型的加權系數。
1.2 正權綜合法
最小二乘準則下的最優權重可能出現負值,這與實際往往不相符合。所以在約束條件中增加正權重約束以得到次優的權重組合。常用的正權組合類型有算術平均法、方差倒數法和均方倒數法。
(1)算術平均法也可稱為等權平均法,即對各模型賦予相同的權重。該法計算簡單,應用較為普遍。
(2)方差倒數法的權重是單個模型的方差倒數與所有模型的方差倒數和的比例。
(3)均方倒數法的權重是單個模型的方差倒數的均方與所有模型的方差倒數的均方和的比例。
1.3 AFTER算法
2001年愛荷華州州立大學的Yuhong Yang提出了一種新的組合預測方法,即AFTER算法 (Aggregated Forecast Through Exponential Reweighting),這種算法計算權重只依賴于過去的預測值和觀測值,因此被稱為AFTER算法。令Y1,Y2,…,Yn為觀察序列,權重為 Wj,n,當 n=1 時,Wj,1=1/J ;當n≥2時,權重為:

其中:

2 我國月度PPI時間序列分析建模
2.1 數據來源
通過查閱 2001~2010年的《中國統計年鑒》,得到了我國 2001年 1月~2010年7月的工業品出廠價格指數,具體的數據如表1所示。
2.2 單項預測法方法

表1 工業品出廠價格指數

表2 ARIMA(2,1,4)模型系數

表3 ARIMA(5,1,1)模型系數

表4 ARIMA(2,1,7)模型系數
對以上數據建立單項預測模型,即自回歸移動平均模型ARIMA(p,d,q),通過比較每次模擬模型的 AIC值,我們選取AIC值最小的三個模型,分別為 ARIMA(2,1,4)、ARIMA(5,1,1)以及 ARIMA(2,1,7),運用 R軟件估計自回歸移動平均模型,得到模型的系數如表2、表3、表4所示。

圖1描述的是工業品出廠價格指數自回歸移動平均模型 ARIMA(2,1,4)、ARIMA(5,1,1)以及 ARIMA(2,1,7)的 預 測圖,其中點代表的是實際的觀測值,而實線是自回歸移動平均模型的預測值,從預測圖上可以看出這三個單項自回歸模型預測的結果還不錯,大部分的預測實線都穿過了實際觀測值,但是還有有一部分實線段明顯超出了實際觀測值的范圍。通常單項預測方法會忽略某一方面因素或是對某種預測的不適應,從而導致單項預測的精度大大下降。如果進行組合預測的話,則可以通過增加模型的個數并且把各個模型加權組合起來,從而達到提高組合預測精度的目的,一般單項預測模型的精度越高其組合預測的精度也越高。
2.3 組合預測法方法
為了提高以上建立的單項預測模型的精度,針對以上建立的三個自回歸移動平均模型建立組合預測模型。本文中我們分別采用算術平均法、方差倒數法、最優加權法和 AFTER法建立組合預測模型,運用 R軟件計算各種方法預測模型的權重:由于算術平均法對每個模型賦予相同的權重,因此有w1=w2=w3=1/3。利用模型估計得到的殘差就可以算出方差倒數法的權重,方差倒數法的權重分別為w1=0.3068002,w2=0.3663674,w3=0.3268324。一旦殘差算出來了,我們就可以根據殘差陣算出最優加權法的權重,分別為w1=-0.4091075,w2=0.9448174,w3=0.4642901。計算 AFTER算法的權重只需知道以上單項模型估計得到的殘差就可,那么從AFTER算法的計算公式中看出它是對每個模型的每一個觀測值賦予一個權重,因此一共有345個權重。
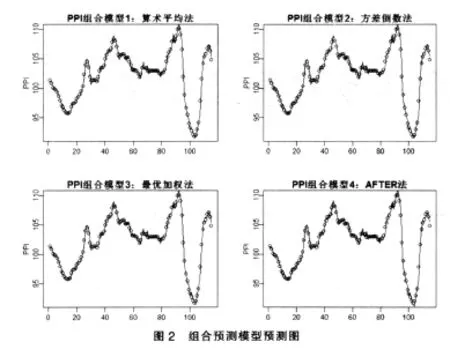
圖2描述的是組合預測模型的預測圖,其中點代表的是實際的觀測值,而實線是組合預測模型的預測值,和單項自回歸移動平均模型預測圖相比較組合預測模型預測的更好一些,組合預測模型預測圖中實線幾乎和所有的點重合了,而單項預測模型預測圖中存在一部分線段超出了實際觀測值的界限。因此組合預測法的擬合精度明顯高于單項預測法的擬合精度。
3 組合預測法的評價
為了更好地評價組合預測法,必須制定一套切實可行的指標來檢驗組合預測效果的好壞,對組合預測效果進行全方位的綜合性衡量和評價。按照預測效果評價原則和慣例,本文提供以下評價指標作為參考,其中 Yt是實際觀測值,Y^t是預測值;n為實際觀測值個數。
(1)均方誤差(MSE):均方誤差就是各測量值誤差的平方和的平均值的平方根。
(2)平均相對誤差(MPE):它度量的是相對誤差的平均值,而相對誤差是絕對誤差與測量值或多次測量的平均值的比值。
(3)Theil不等系數(U):Theil不等系數衡量預測模型預測能力指標,0≤U≤1,當U→0時說明預測精確度高,U→1時說明預測的精確度較低.Theil不等系數計算公式如下:
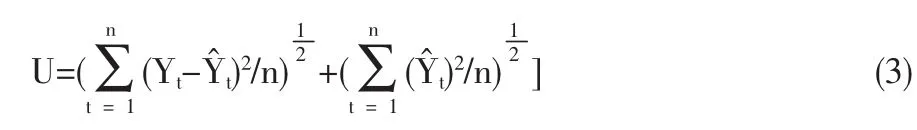
(4)凈均方預測誤差ANMSEP(net mean square prediction error):下的條件均值,凈均方預測誤差值越小說明模型預測的越好。四種組合模型預測結果的精度如表5所示。

對比一下在這四種組合預測模型的預測評價指標,最優加權法的組合預測模型的均方誤差、平均相對誤差、Theil不等系數以及凈均方預測誤差的取值都是最小的,從這個角度
其中mi為 Yi在先前觀測值可以看出最優加權法的組合預測模型擬合效果不錯;其次AFTER算法的預測評價指標值都小于算術平均法和方差倒數法的預測評價指標,說明 AFTER算法的組合預測模型優于算術平均法和方差倒數法的組合預測模型。盡管最優加權法的預測評價指標值都是最優的,但是前面我們算出最優加權法的權重 w1=-0.4091075為負數,顯然這是沒有實際的經濟意義,因此綜合評價預測指標我們得出 AFTER算法的組合預測模型是最優的。

表5 組合模型預測精度表
運用 AFTER算法進行組合預測得到的預測值的預測誤差均低于 2.52%,遠遠小于 10%,因此用 AFTER算法進行組合預測是科學的。最后運用 AFTER算法對我國 2010年月度 PPI進行外推預測,預測得到 2010年 8月的 PPI為 103.82118,最近國家統計局公布出 2010年 8月份的PPI為 104.1,預測誤差僅為 0.45%。這進一步證明了用AFTER方法進行組合預測是科學的。
4 結論
PPI是我國物價測度指標體系的核心組成部分,是判斷宏觀經濟走勢的重要經濟指標,它能夠靈敏的反映社會供求變化。本文基于我國 2001年 1月~2010年 7月的月度PPI數據建立 ARIMA模型進行單項預測,然而采用單項預測模型難以做到充分利用已有的信息資源,預測能力欠缺。為了充分利用信息、全面提高預測精度,本文運用算術平均法、方差倒數法、最優加權法以及 AFTER算法這四種組合預測法對我國月度 PPI進行組合預測,并且運用均方誤差、平均相對誤差、Theil不等系數以及凈均方預測誤差這四個預測效果評價指標來比較四種組合預測法的預測精度,最后得出 AFTER算法是最佳的。運用該方法進行外推預測,預測結果顯示 2010年 8月份的 PPI預測誤差僅為 0.45%,表明該方法是科學的。
[1]PPI,百度百科[EB/OL].http://baike.baidu.com/view/101651.htm.
[2]唐小我.最優組合預測的計算方法[J].管理現代化,1992,(1).
[3]李學全.最優組合預測非負權系數的計算方法研究[J].預測,1995,60(4).
[4]Zhuo Chen,Yuhong Yang.Time Series Models for Fore Casting:Testing or Combining?[J].Studies in Nonlinear Dynamics&E-conometrics,2007,11(1).
[5]國家統計局數據庫[EB/OL].http://www.stats.gov.cn/tjsj/ndsj/.
[6]王黎明,王連.應用時間序列分析[M].上海:復旦大學出版社,2009.
[7]王斌會.R語言統計分析軟件教程[M].北京:中國教育文化出版社,2006.
[8]周巧.湖北省GDP總量的時間序列預測模型的比較分析[J].中南財經政法大學研究生學報,2009,(4).
[9]Hui zou,Yuhong Yang.Combining Time Series Models for Forecasting[J].Internayional Joural of Forecasting,2002,(2~4).

