滾動導軌結合面動態特性參數識別實驗研究

張 華 袁軍堂 汪振華

南京理工大學,南京,210094

0 引言

對于數控機床而言,滾動導軌是廣泛應用的功能部件。由于滾動結合面為線接觸或點接觸,剛度相對較弱,往往是數控機床整體結構的薄弱環節,從而影響數控機床的加工精度。為了準確獲取滾動導軌結合面動態特性參數,國內外學者進行了相關探索與研究[1-5]。本文建立了識別滾動導軌結合面動態特性參數的測量模型,該測量模型將安裝有滾動導軌的機構簡化為單自由度系統并消除了基礎位移對參數識別的影響。基于測量模型研制了滾動導軌結合面動態特性參數測量裝置,并針對施耐博格MRC45型導軌進行了實驗,獲得了其法向和側向動態剛度及阻尼數據。

1 滾動導軌結合面動態特性建模

一般情況下,滾動導軌安裝在基座(如機床床身)上,而運動部件(如工作臺)連接在滑塊上。滑塊和導軌之間通過滾動體(如滾珠、滾柱)連接,它們之間為點接觸或線接觸,而導軌與基座以及運動部件與滑塊之間都為螺栓連接,剛度遠大于導軌—滾動體—滑塊之間滾動接觸面的接觸剛度。因此,通過合理設計,增大基礎和運動部件的剛度,在一定的振動頻率范圍內可以將基礎部件和運動部件視為剛性體。這樣就可將運動部件及滑塊看成質量塊,滾動結合面看作彈性及阻尼元件,從而可得到如圖1所示振動系統。

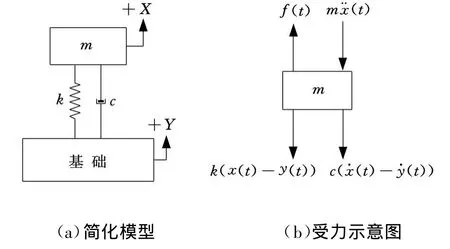
圖1 力學模型

對于圖1a所示系統,當質量塊m受到外界簡諧激振力f(t)作用時,系統受力情況如圖1b所示,其振動方程可以表示為

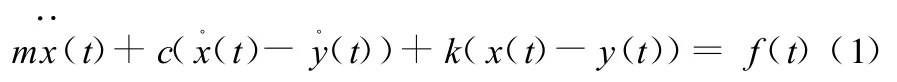
式中,m為運動部件與滑塊的總質量;k、c分別為滾動導軌結合面的剛度和阻尼;x(t)、y(t)分別為質量塊和基礎的位移。

對式(1)作以下變換構成單自由度振動方程：

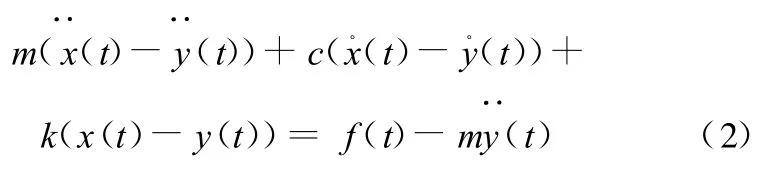
在簡諧激振力作用下,f(t)、x(t)及y(t)可用復向量表示 ：f(t)=F ejωt,x(t)=X ejωt,y(t)=Y ejωt(F 、X 、Y 分別表示f(t)、x(t)和 y(t)的有效值和初始相位)。將以上三項代入式(2)可得

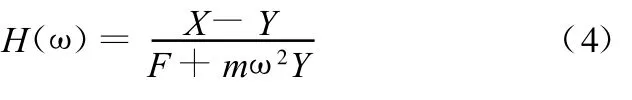
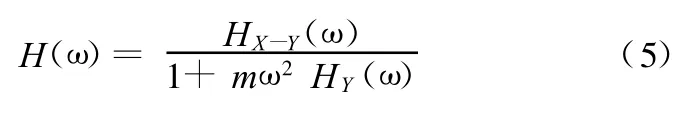
式中,HX-Y(ω)為運動部件頻響函數與基礎頻響函數差;HY(ω)為基礎頻響函數。

HX-Y(ω)和 HY(ω)可由實測數據計算得到。由以上推導可知,H(ω)是一個等效單自由度系統的頻響函數,等效單自由度系統的質量m為運動部件與滑塊的總質量,剛度和阻尼分別為滾動導軌結合面剛度和阻尼。由頻響函數曲線可識別出系統固有頻率ωn,然后可根據下式求出滾動導軌結合面的動態剛度及阻尼：

阻尼比ξ可根據H(ω)幅值曲線采用半功率帶寬法求取。如圖1b所示,基礎位移影響彈簧和阻尼器的受力狀況,本文從力學模型中消除基礎位移的影響更符合實際,識別出的參數精度高且具有理論依據。

2 測試系統設計

根據測量模型設計了滾動導軌結合面動態特性參數測試裝置,圖2所示為法向激振時測試裝置結構圖,測試裝置采用雙導軌結構,通過橋板連接兩滑塊,激振器在橋板上表面中心位置對裝置進行激振。側向激勵點如圖2中的9所示 ——為便于側向加載,在橋板另一側對稱加工了阻抗頭連接螺紋孔,用于側向激振。

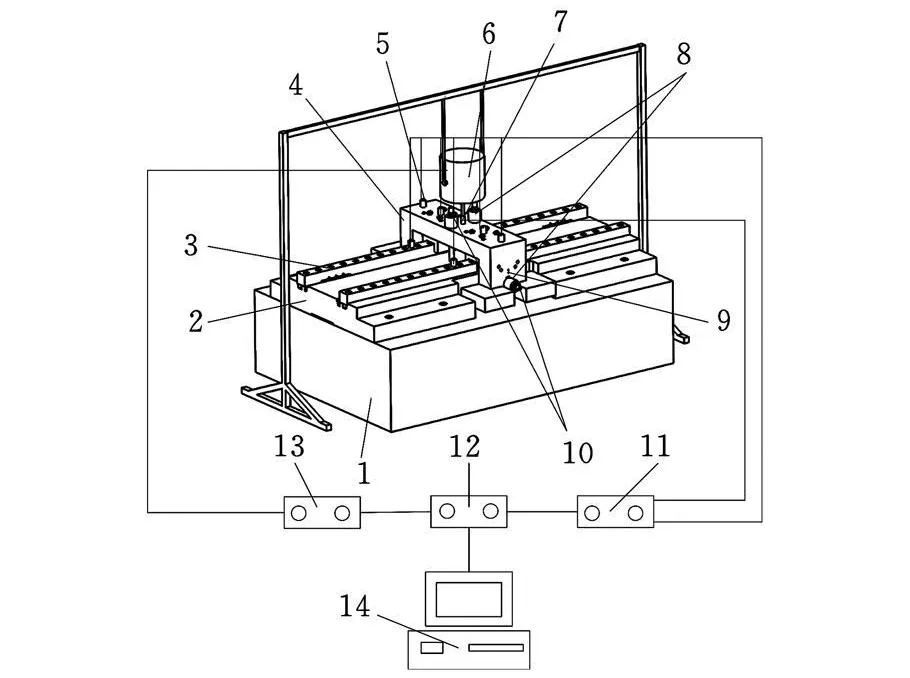
圖2 測試裝置結構圖

如圖2所示,測試時首先在模態分析軟件14中設置各參數,數字采集器12發出的掃頻信號經功率放大器13放大后傳送至激振器6,激振器連接阻抗頭7并對實驗臺激勵。力信號由阻抗頭拾取,加速度信號由加速度傳感器5測得,兩者經電荷放大器11后轉變為適量大小的電壓信號,并由數據采集器采集。計算機最終得到的是經數據采集器模數轉換的力和加速度值,通過模態分析系統傅里葉變換后即可獲得各測點頻響函數。測試儀器的型號和主要參數見表1。

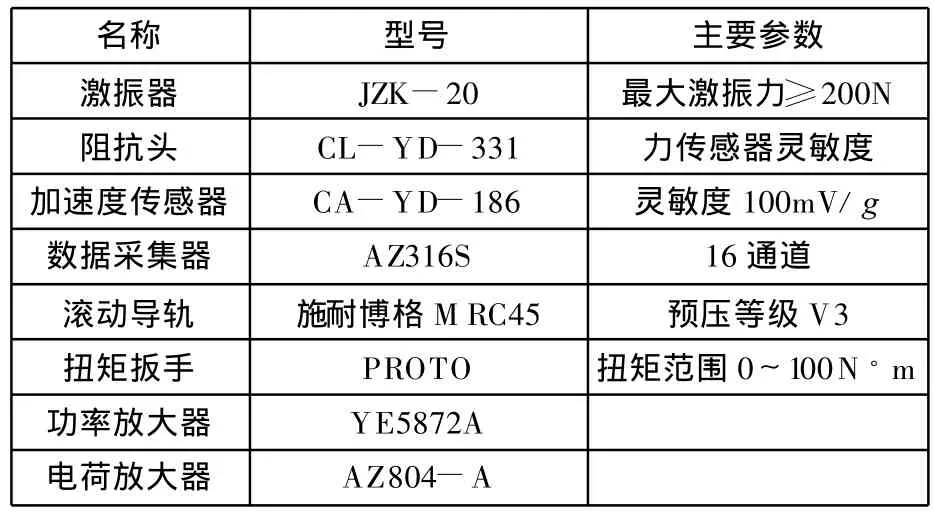
表1 模態試驗儀器

3 測試結果與分析

3.1 系統測試

為驗證測試系統的準確性,對實驗導軌在未加載狀態下(載荷僅為橋板重量)側向動態剛度及阻尼進行測量與識別,通過對系統振型、測點頻響函數及H(ω)曲線的檢驗來判別測試結果的準確性。

系統振型從以下兩方面檢驗：一是測量模型中將橋板及滑塊視作整體,因此橋板與滑塊應保證同步平動;二是對于兩自由度無阻尼系統,在簡諧激振力作用下,兩質點以相同的頻率和相角但不同的振幅做簡諧振動。圖1a簡化模型中,阻尼值c較小,系統為弱阻尼系統,因此在系統固有頻率下橋板與滑塊應和基礎近似做相對平動。本文所使用的安正CRAS模態分析軟件振型動畫功能可顯示各測點相對運動關系,因此在橋板、滑塊及基礎上合理布置測點,測試結束后就可觀察它們之間的相對運動關系,經檢驗測試裝置在450Hz附近振型滿足以上要求。

頻響函數HX-Y(ω)、HY(ω)以及 H(ω)都由測點實驗數據計算得到,因此測點實驗數據準確可靠對識別結合面動態特性參數至關重要。根據測量模型,橋板和基礎測點頻響函數曲線都應為單自由度曲線;本文振動信號由加速度傳感器測得,因此橋板和基礎測點頻響函數幅值A1及 A2都為加速度和力的比值。

圖3 橋板測點頻響函數曲線

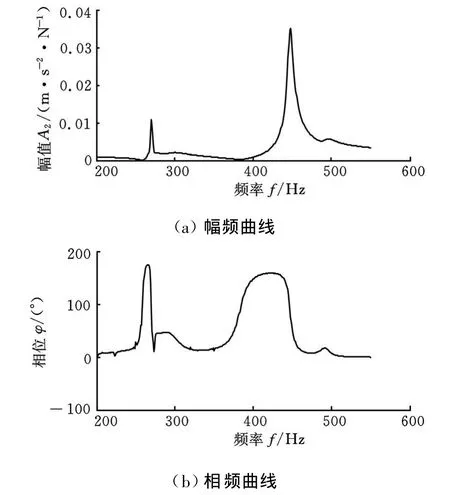
圖4 基礎測點頻響函數曲線

圖3、圖4所示分別為橋板與基礎上某測點頻響函數曲線。從圖中可以看出：在270Hz及450Hz附近頻段內兩者都為較好的單自由度曲線,但270Hz頻率點處橋板振型為兩側擺動型,為橋板自身模態,不符合上文所述振型要求。圖5為根據式(5)計算得到的H(ω)幅頻和相頻曲線 ——求取H(ω)時對測得的加速度進行了二次積分,因此 H(ω)幅值A3為位移和力的比值。從圖5可以看出,幅頻曲線在450Hz附近達到峰值,相位在峰值頻率附近發生了180°轉變,為典型的單自由度振動曲線。

將系統固有頻率ωn代入式(6)可以得到未加載狀態下該滾動導軌結合面側向動態剛度kc=3.6×108N/m。阻尼比ξ可由半功率帶寬法求取,根據 H(ω)幅頻曲線計算得到該滾動導軌未加載時側向阻尼比ξc=0.64%,側向阻尼值cc=1678 N?s/m。法向剛度和阻尼的測量與側向類似：未加載狀態下導軌結合面法向動態剛度 kf=3.7×108N/m,法向阻尼比ξf=0.54%,法向阻尼值c f=1388N?s/m。

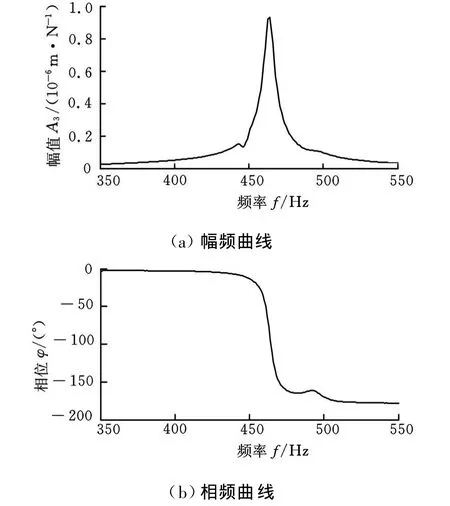
圖5 等效單自由度系統頻響函數曲線

3.2 載荷對滾動導軌結合面動態特性參數的影響

對于機床而言,安裝在導軌上的運動部件重量各異,而且加工工件重量及切削力也會發生變化,因此滾動導軌所受載荷會隨著不同的加工狀態發生變化,分析不同載荷下滾動導軌結合面動態特性參數的變化規律對指導機床設計具有重要意義。如圖2所示：M12雙頭螺栓10連接安裝平臺2和橋板4對導軌法向及側向進行組合加載,為了減小螺栓對剛度測量的影響,在施力螺栓上加上較厚的橡膠圈8;測量時通過扭矩扳手調節施力螺栓預緊力對滾動導軌結合面進行加載,預緊力F≈T/(0.2d),d為施力螺栓公稱直徑,T為扭矩。圖6所示為實驗導軌結合面動態剛度隨載荷變化曲線圖。由圖6可知：①導軌結合面側向動態剛度隨載荷增大而緩慢增大,當載荷達到一定值后剛度趨于穩定,剛度最大變化量在10%左右;②法向動態剛度受載荷影響不明顯,剛度在3.75×108N/m左右變化。

4 結論

(1)建立了識別滾動導軌結合面動態特性參數的測量模型,該測量模型將安裝有滾動導軌的機構簡化為單自由度系統并消除了基礎位移對參數識別的影響。根據測量模型研制了滾動導軌結合面動態特性參數識別實驗裝置,獲得了滾動導軌法向及側向動態剛度精確測量方法。

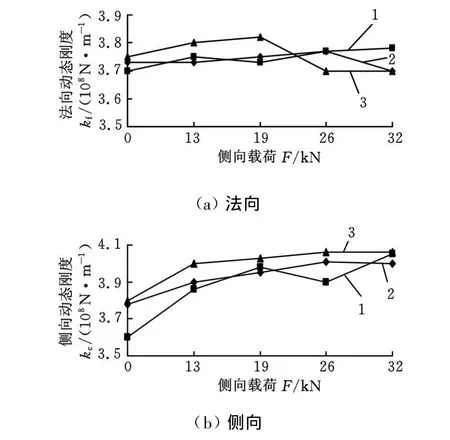
圖6 載荷-剛度變化曲線

(2)實驗導軌結合面側向動態剛度隨載荷增大而緩慢增大,當載荷達到一定值后剛度趨于穩定,剛度最大變化量在10%左右;法向動態剛度受載荷影響不明顯,剛度值保持在3.75×108N/m左右。

[1] 王延忠,周元予,劉強,等.直線電機驅動的加工中心導軌副動力學特性分析[J].中國機械工程,2008,19(13)：1574-1576.

[2] 張建潤,盧熹,孫慶鴻,等.五坐標數控龍門加工中心動態優化設計[J].中國機械工程,2005,16(21)：1949-1953.

[3] Liu Yang,Li Jingkui.Influence of Linear Guide Joint on Dynamic Behavior of NC Machine Tools[J].Journal of Northeastern University(Natural Science),2006,27(12)：1369-1372.

[4] 張廣鵬,史文浩,黃玉美.機床導軌結合部的動態特性解析方法及其應用[J].機械工程學報,2002,38(10)：114-117.

[5] 李磊,張勝文,于洋,等.滾動導軌結合面參數識別及仿真分析[J].江蘇科技大學學報,2009,23(2)：142-145.