基于層次結構模型的小樣本組合預測建模

謝 力,魏汝祥,1b，尹相平，訾書宇

（1.海軍工程大學 a.裝備經濟管理系；b.理學院，武漢430033；2.海軍裝備部 裝備招標中心，北京 100071）

0 引言

在預測的實際工作中，有時會碰到一些樣本小、波動大的情況，如果直接對其進行預測，往往容易出現擬合效果好而預測效果差的情況。1969年，Bates和Granger[1]提出的組合預測方法，將各種單個預測看作代表不同的信息片段，通過信息的集成分散單個預測特有的不確定性和減少總體不確定性，從而提高預測的精度。目前，關于組合預測的研究主要集中于對同一組數據采用不同預測方法得到的預測結果進行組合，或者對不同來源的性質相異的數據分別建模得到的預測結果進行組合。在這兩種研究中，一般認為因為后者利用的信息有本質上的差異，故其組合的效果更佳[2-4]。而要得到多種不同來源、可直接為預測所用的信息往往代價很大或者根本不可行。而實際上，待預測變量的時間序列以及其層次結構的各時間序列往往容易得到。Armstrong[5]、Phelps[6]等人研究發現，分解可以將看起來很難的信號變得簡單化。Zellner等人[7]關于GDP增長率以及Marcellino等人[8]對幾種歐洲宏觀經濟變量的預測結果也顯示，分解能改進預測的性能。García[9]、Karsten[10]等人分別在交通事故率和歐洲宏觀經濟變量預測的研究中，都發現使用不同層次信息建模能顯著改善預測的效果。George[11]、Mauro[12]等人也對分層組合預測進行了一定的研究。這些研究盡管都涉及到了層次結構的組合預測，但僅局限于對預測變量下層結構分解和綜合的研究，事實上，變量的整個層次結構都攜帶了關于變量的有關信息，應該綜合考慮。層次結構模型中的上層結構從更加綜合的角度也攜帶了變量的大量相關信息，且變量本身時間序列所具有的特征也不能忽視。因此，本文主要嘗試根據層次結構模型的各種時間序列分別進行預測，從不同層次結構的角度對某一變量進行預測，將不同層次的預測結果與變量本身時間序列預測結果進行組合，以充分利用各相關時間序列所包含的信息，提高小樣本預測的穩定性，降低預測風險。

1 層次結構模型

任何系統都是層次分明、有序的結構系統，通過層次結構的構建可以解釋其有序結構的內在規律。層次結構模型往往可以把一個復雜的問題通過分解或綜合成若干個簡單的問題，通過解決一個個簡單問題，達到解決復雜問題的目的。其中層次分析法實際上就是主觀判斷分解的一個非常成功案例。

變量的層次結構實質上是包含了分解和綜合兩個方面。在時間序列的預測過程中，一個看起來沒有什么規律的復雜時間序列，通過層次結構的分解后（下層結構），各成分的時間序列可能規律就比較明顯了，成分序列的細節也就會顯現出來；同樣，通過層次結構中的綜合（上層結構）后，也有可能使整體規律更加清晰。層次結構組合預測，先根據主觀判斷對預測對象構建層次結構，然后對層次結構中的各相關對象分別進行預測，根據將來的相關信息對預測結果進行疊加綜合或分解，最后，將通過變量不同層次結構以及相應預測結果與變量原始數據獲得的預測結果進行組合，得到最終預測結果。

2 小樣本層次結構組合預測建模

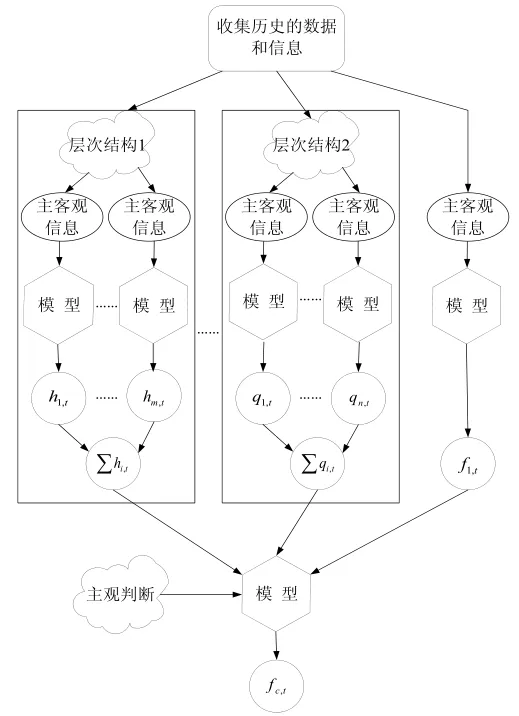
組合預測最根本的思想就是充分的利用可獲得的信息，提高預測的穩定性，降低預測的風險。在預測的實際工作中，盡管要得到多種不同來源、可直接為預測所用的信息往往代價很大或者根本不可行，但預測變量的時間序列以及其層次結構的各時間序列往往容易得到，我們可以充分利用其層次結構各序列的信息來進行組合預測（見圖1）。

2.1 層次結構構建

在小樣本層次結構預測的研究中，由于過高層次的樣本往往規律比較復雜，難以準確把握；而過低層次的數據樣本往往受噪聲的影響會較大，預測的誤差也會增大。因此，為了從層次結構中獲得有用的信息，降低噪聲對過低層次樣本的影響和更高層次綜合樣本信息損失的風險，通常僅考慮待預測變量的鄰近層次預測的結果，即向下一層結構和向上一層結構（圖2）。

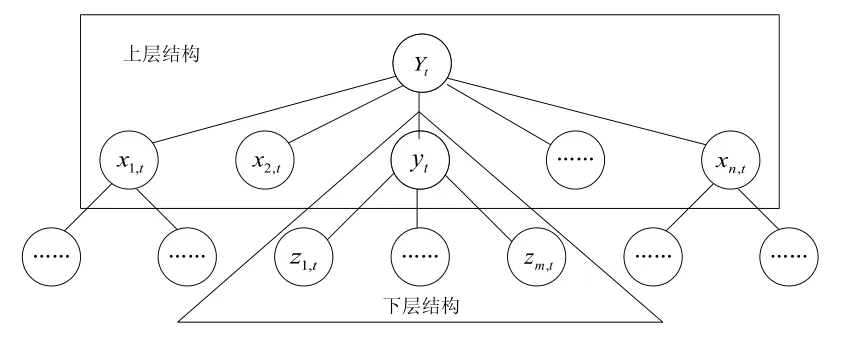
圖2 層次結構模型

2.2 上層結構建模

在層次結構模型的上層結構中，設t時刻待預測變量的值為yt，上層綜合變量為Yt，構成Yt的其他n個子項分別為xi,t，i=1,…,n。則有

根據上層結構的各子項相關信息（可以是主觀判斷和各項費用相應的影響因素，也可以是時間序列等），分別構建如下預測模型：

那么，上層結構中，待預測變量yt的預測模型可以表示為

2.3 下層結構建模

在層次結構模型的下層結構中，待預測變量yt可分解為m個子項，分別為zj,t，j=1,…,m。則有

根據下層結構各子項相關信息，分別構建如下預測模型：

那么，向下分解的裝備維修費的預測模型可以表示為

2.4 組合預測建模

設t時刻待預測樣本數據為yt，通過p種不同方式得到上層結構預測分別為，k=1,…,p；通過q種不同方式得到下層結構的預測值分別為，l=p+1,…,p+q；不分解直接進行預測得到待預測變量的預測值為則yt的組合預測可以表示為

常用的組合預測模型有等權組合、最優方差組合和基于回歸的組合等線性組合模型[2-4]，此外，神經網絡、模糊系統、遺傳規劃、自組織算法和神經-模糊系統等非線性組合預測模型也得到了飛速的發展[14]。

3 應用實例

本部分以美國CVN68航母基地級維修費進行預測為例，來驗證本文提出方法的有效性。

3.1 層次結構構建

為了簡化計算，這里僅選擇一種向下分解和一種向上分解方式。根據文獻[15]，美國航母維修費主要包括中繼級維修費用和基地級維修費用等兩部分。基地級修理又可以分為計劃修理費用、非計劃修理費用和艦隊現代化費用。因此，基地級維修費向下可以分解為計劃修理費用、非計劃修理費用和艦隊現代化費用；在其向上分解結構中，CVN68的年度維修費由基地級維修費和中繼級維修費構成，各相應的數據見表1。這里我們主要考慮短期預測的情況，選取1978～1994年數據進行建模，并用1995年的數據來測試方法的有效性。

3.2 層次結構預測建模

在García等人[10]的研究中，發現通過分解模型，采用簡單方法與更加復雜的方法表現一樣好，為了簡化計算，所有的預測使用Holt的指數平滑法，運用Eviews 6.0計算。

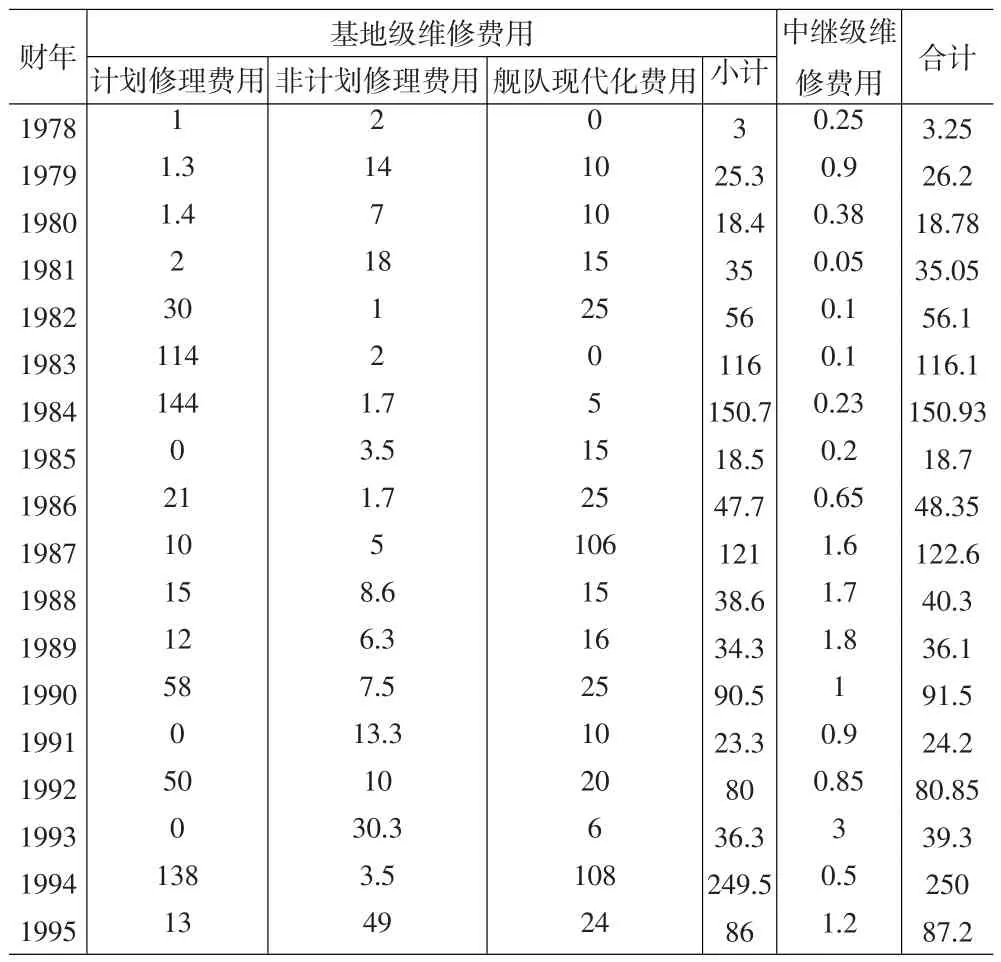
表1 CVN68年度維修費數據 （98財年，百萬美元）

3.2.1 上層結構建模

從表1中的數據可以看出，中繼級維修費用遠小于基地級維修費用，相差近100倍，故在向上分解結構中，CVN68年度維修費數據規律主要表現為基地級維修費，分解建模意義不大，故該實例中，我們不對向上分解進行建模。

3.2.2 向下分解建模

(1)計劃修理費用

根據計劃修理的特征，我們認為計劃修理一般具有一定的周期，盡管我們不知道美國航母計劃修理的確切周期，但從表1中的數據，可以看出其周期應該在7左右，故在采用Holt的指數平滑法建模預測時，選擇其季節性周期為7，Holt-Winters-Additive模型。

(2)非計劃修理費用

非計劃修理費用一般沒有明顯的季節性，故選擇Holt-Winters-No seasonal模型。

(3)艦隊現代化費用

根據艦隊現代化費用特征，從表1中的數據，可以看出其周期應該在4左右，故在采用Holt的指數平滑法建模預測時，選擇其季節性周期為4，Holt-Winters-Additive模型。

(4)主觀判斷分解預測的綜合

根據（5）式，對計劃修理費用、非計劃修理費用、艦隊現代化費用預測結果進行綜合。

3.2.3 基地級維修費直接建模

由于基地級維修費分解子項的周期性差異較大，所以基地級維修費時間序列沒有明顯的周期，選擇Holt-Winters-No seasonal模型。

3.3 組合預測

由于等權組合預測計算簡單，且在大量組合預測的實證研究中表現出一定的優勢[6-7]，這里我們也選擇等權組合預測模型對分解預測和直接預測的結果進行組合。組合預測與各單項預測以及原值的比較如圖3。

1995年各方法預測值如表2。

表2 1995年預測結果比較

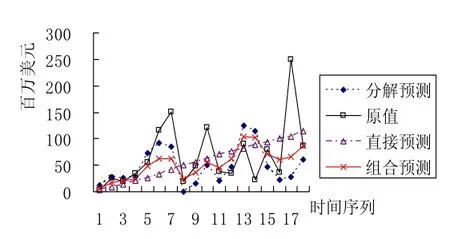
圖3 各種預測方法預測效果比較

從表2中可以看出，對于1步向前外推預測，直接預測和分解預測效果相當，且都不太好，而它們的組合預測效果明顯得到改進。

4 結束語

（1）本文的建模過程適用于不確定性大、樣本小且波動大，相關層次結構信息易獲取的預測問題；

（2）基于層次結構模型的組合預測，在整個建模的過程中，能充分利用各層次序列的信息，進而提高小樣本預測模型的穩定性，降低預測風險；

（3）在各層次結構序列的特征不太明顯，且不能夠反映出相應綜合性項目所不具有的特征情況下，采用層次結構預測與直接預測差異將不大，層次結構預測失去相應的價值。

（4）本文建模中采用的是加法形式的分解與綜合，盡管Collopy等人[16]指出分解成分的乘法綜合可能帶來爆炸性的誤差，具有很大風險，但在特點的背景下，也可以嘗試采用乘法形式的分解與綜合來進行研究。

[1] Bates J M,Granger C W J.Combination of Forecasts[J].Operations Research Quarterly,1969,20(4).

[2] Armstrong J S.Combining Forecasts:The End of the Beginning or the Beginning of the Eend[J].International Journal of Forecasting,1989,(5).

[3] Graham E,Clive W J G,Allan T.Handbook of Economic Forecasting(Volume I)[M].Netherlands:Amsterdam:Elsevier,2006.

[4] 汪同三,張濤.組合預測——理論、方法及應用[M].北京社會科學文獻出版社,2008.

[5] WANG Tong-san,Zhang Tao.Forecast Combination:Theory,Method and Application[C].Social Sciences Academic Press,2008.

[6] Armstrong J S,Denniston W B,Gordon M M.The Use of the Decomposition Principle in Making Judgements[J].Organisational Behaviour and Human Performance,1975,(14).

[7] Phelps R H,Shanteau J.Livestock Judges:How Much Information can an Expert Use?[J].Organisational Behaviour and Human Performance,1978,(21).

[8] Zellner A,Tobias J.A Note on Aggregation,Disaggregation and Forecasting Performance[J].Journal of Forecasting,2000,(19).

[9] Marcellino M,Stock J,Watson M.Macroeconomic Forecasting in the Euro Area:Country Specific Versus Area-wide Information[J].European Economic Review,2003,(47).

[10] Poncela P,Garcia-Ferrer A.The Effects of Disaggregation on Nonstationary I(1)time Series[R].Universidad Autónoma de Madrid,DAEII,Mimeo,2005.

[11] García-Ferrer A,de Juan A,Poncela P.Forecasting Traffic Accidents Using Disaggregated Data[J].International Journal of Forecasting,2006,(22).

[12] Karsten R.Macroeconomic Forecasting in the EMU Does Disaggregate Modeling Improve Forecast Accuracy?[J].Journal of Policy Modeling,2008,(30).

[13] George A,Roman A A,Rob J H.Hierarchical Forecasts for Australian Domestic Tourism[J].International Journal of Forecasting,2009,(25).

[14] Mauro C,Carmine P.A Hierarchical Procedure for the Combination of Forecasts[J].International Journal of Forecasting,2010,26(4).

[15] Christiane L,Bogdan G.Review of Nature-inspired Forecast Combination Techniques[R].United Kingdom:Bournemouth University,2008.

[16] Birkler J,Michael M,John S,et al.The U.S.Aircraft Carrier Industrial Base:Force Structure,Cost,Schedule,and Technology Issues for CVN77[R]. Santa Monica, Calif: RAND Corporation,MR-948-NAVY/OSD,1998.

[17] Collopy F,Armstrong J S.Decomposition by Causal Forces:Using Domain Knowledge to Forecast Highway Deaths[C].Working Paper,1993.