同一個問題 不同的角度

430040 武漢市吳家山第三中學 吳 波

越來越多的中考壓軸題，在二次函數的圖象拋物線上架構幾何圖形，學生感覺難度較大，主要原因是思維水平跟不上.本文就充分應用習題，最大限度發揮習題的效應，發展學生的思維作一拋磚引玉，以期待各位同仁的指導.

題目如圖1，拋物線y=－x2+2x+3與x軸交于A，B兩點，交y軸正半軸于C點，D為拋物線的頂點，點P在OB的延長線上，且∠PCB=∠CBD，求點P的坐標.

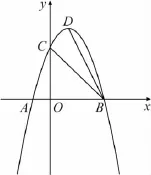
圖1

1 不同的角度求解，培養學生求異思維

前期基礎分析已知拋物線解析式，能夠求出A，B，C，D四點的坐標，A(－1，0)，B(3，0)，C(0，3)，D(1，4)，要求點P的坐標，由于點P的位置在x軸上，可將其坐標轉化成求線段OP的長，或者把點P看作某條直線與x軸的交點，我們需要求出這條直線的解析式.

思路1首先根據點C，點B的坐標，發現∠OBC=∠OCB，那么它們的鄰補角也相等.結合條件∠PCB=∠CBD，那么涉及到的∠PCB和∠CBP構成了△PCB，以它為模板構造三角形全等.

略解1(如圖2)延長BD交y軸于點Q.

∵OC=OB，

∴∠OBC=∠OCB，

∴∠CBP=∠BCQ，

又BC=CB，∠PCB=∠CBQ，

∴△CBP≌△BCQ，

∴BP=CQ，∴OP=OQ，

∵B(3，0)，D(1，4)，

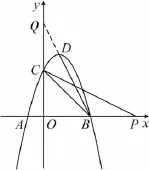
圖2

∴直線BD的解析式為y=－2x+6，

∴Q(0，6)，

∴P(6，0)

思路2(如圖2)發現∠OCB=∠OBC后，結合∠PCB=∠CBD，可以得到∠PCO=∠DBO，而∠PCO，線段OP可以得到直角△PCO，以它為模板構造三角形全等.

略解2同上解，證△COP≌△BOQ即可.

點評上述兩種思路，將點P的坐標轉化成求線段的長度，將線段置入三角形，構造出三角形全等，利用已知坐標求出線段的長，思維流暢，構造順理成章.

思路3(如圖3)由∠PCB=∠CBD，若標出PC與BD的交點M，則可得到MC=MB.容易得到∠MCO=∠MBO，若連接OM，得到△OMC≌△OMB.若能求出點M的坐標，就可以求出直線CM的解析式，從而求出點P的坐標.

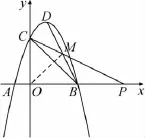
圖3

略解3連OM，易證△OMC≌△OMB，

∴∠COM=∠BOM，

∴直線OM的解析式為y=x，

易知直線BD的解析式為y=－2x+6，

∴M(2，2)，又C(0，3)，

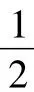
∴P(6，0).

點評從解析法的角度開始思考問題，關鍵是找出直線PC上的另一點，求出直線PC的解析式，再求點P的坐標.由條件∠PCB=∠CBD得等腰三角形CMB，可嘗試其頂點M作為直線PC上的另一點.進而思考頂點M的坐標求法.構造易，思維指向性很強，步步逼近目標求解.

思路4我們很容易發現∠PCO=∠DBO.要求點P的坐標，就是求線段OP的長，而線段OP在直角△PCO中，嘗試構造一個包含∠DBO的直角三角形.

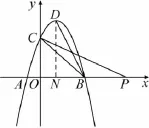
圖4

略解4(如圖4)作DN⊥OB，垂足為N，

易證△PCO∽△DBN，

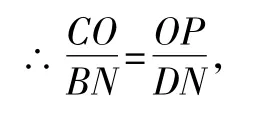
易知線段CO=3，BN=2，DN=4，

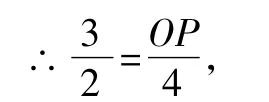
∴OP=6，即P(6，0)

點評點P坐標轉化成線段OP的長，目標轉換很準確，思維很大膽，構造簡單直接.

思路5(如圖5)要求點P的坐標，轉化成求直線CP的解析式，因為點C坐標已知，從而轉化成求直線CP上另一點的坐標.怎樣找這一點呢?經過演算，可發現點B，C，D構成一個直角三角形，于是過點B作BE⊥BC交PC于點E，構造△DCB≌△EBC.若能求出點E的坐標，就可以求直線CE的解析式，從而求出點P的坐標.要求點E坐標，就先作垂線.過點D，E分別作出坐標軸垂線，得△DCM≌△EBN，可求出BN，EN，從而求出點E坐標.

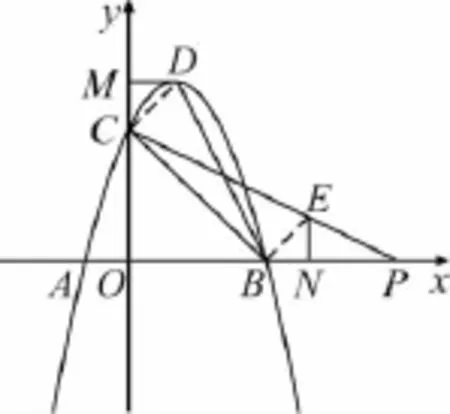
圖5

點評與思路3思考方向一致，發現很深入，但求解很復雜.

以上各種求解思路，涉及全等、相似等基本知識，包含轉化、構造等基本方法，鍛煉學生求異思維.

2 不同的角度提問，培養學生求同思維

變式1假設點P為拋物線上一點，其它條件不變，求點P的坐標.

點評原題中，實際固定了點P的位置.當點P在拋物線上時，則其位置可能在第一象限，也可能在第四象限.在第一象限時，按原題求解，在第四象限時，過點C作BD的平行線交拋物線可求解.這樣變式，培養學生全面思考問題的能力，或者說是分類討論問題的能力.(如圖6)

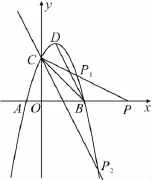
圖6

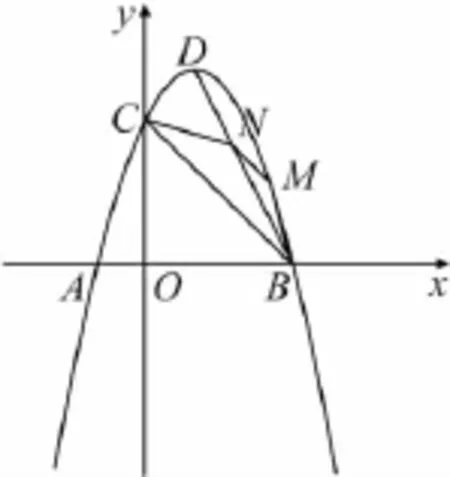
圖7

變式2如圖7，在線段BD上有一點N，在拋物線第一象限上是否存在一點M，使四邊形MNCB為等腰梯形，若存在，求點M的坐標.

點評在拋物線上架構一個等腰梯形，圖形變得復雜，由于點M，點N位置都未定，誰先確定也是一個問題，思維更復雜，學生更難把握.培養學生分析問題，透過現象看本質的能力.(提示：由于四邊形MNCB為等腰梯形，連接MC，則易得∠MCB=∠NBC，和原題一樣.)

圖8

以上各種變式，涉及在拋物線上架構四邊形、與三角函數聯系，從不同角度看問題本質，都可以轉化成原題求解，培養學生的求同思維.

《數學課程標準》提出，數學教學應引導學生通過思考、探索，發展思維，要注重數學知識之間的聯系，不斷豐富解決問題的策略，提高解決問題的能力.多角度地看同一道問題，最大限度讓每一道習題發揮作用，讓學生學會分析、學會構造、學會轉化，能切實培養學生思維的廣度和深度.