例說以連續自然數平方根為邊長的三角形在物理中的應用

丁岳林

(江蘇省常州高級中學,江蘇常州 213003)

在我們研究的物理問題中,很多時候會與角度有關,而通常為討論問題的方便會取一些特殊角,如 θ=30°,θ=45°,θ=60°,還有 θ=37°(或 θ=53°))等.其中 θ=37°(或 θ=53°)是討論矢量運算時的平行四邊形定則最好的實例,即“32+42=52”(滿足勾三股四弦五的直角三角形),而另外的那些大量使用到的特殊角,一般來說都是基于數學上的特殊(相應的角度三角函數為簡單的數值),而沒有真實的物理模型為支撐.本文要討論的是基于真實物理背景的θ=35°(或 θ=55°)的一種特殊角.

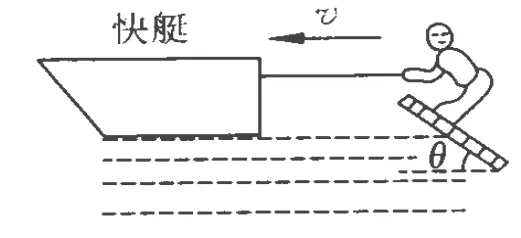
圖1

例1.滑板運動是一項非常刺激的水上運動,如圖1所示,運動員與滑板的總質量為 m,滑板的總面積為 S,水的密度為 ρ.理論研究表明,當滑板與水平方向的夾角為θ(板前端抬起的角度)時,水對板的作用力大小為 N=ρ Sv2sin2θ,方向垂直于板面,式中 v為快艇的牽引速度.求:為使滑板能在水面上滑行,快艇水平牽引滑板的最小速度(忽略水和空氣的阻力).

解析:滑水運動員在快艇牽引下的滑行過程中,會經常變換姿勢,其實,這既是為使運動具有觀賞性,也是出于平衡的需要.滑板與水平方向間的夾角θ與快艇的牽引速度v等都是互相聯系的.要解決“快艇牽引滑板的最小速度”問題,首先需要弄清 S、v、θ等物理量之間的相互關系.

為此,選取滑板與運動員作為研究對象,受力情況如圖2.即滑板與運動員共受到3個力的作用:重力G,水對滑板的作用力N(方向與滑板板面垂直)及繩子對運動員的拉力 F.由平衡條件,豎直方向有

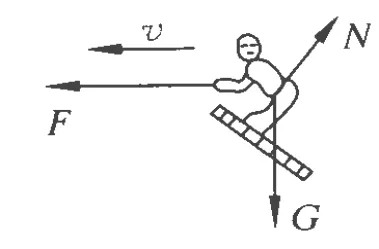
圖2

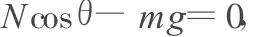
又由題中所給的條件

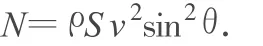
解得牽引速度為

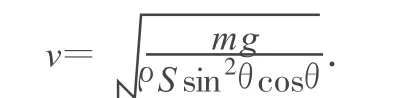
即在運動員與滑板總質量一定、滑板的總面積S一定時,維持滑板平衡所需的牽引速度大小,僅由滑板與水平方向的夾角θ決定.或者說,快艇對運動員與滑板的牽引速度v是滑板傾角θ的函數.當θ取某一值時,牽引速度有最小值.下面我們就來討論這一極值.

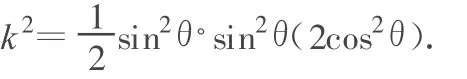
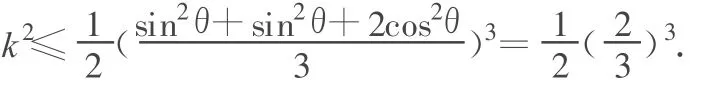
當且僅當 2cos2θ=sin2θ,即 θ=arctan 2=54.7°≈55°時,k有最大值.

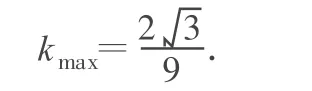
故快艇最小速度的表達式為

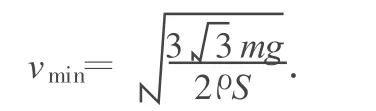
例2.(2008年江蘇高考題)如圖3所示.一根不可伸長的輕繩兩端各系一個小球 a和b,跨在兩根固定在同一高度的光滑水平細桿上,質量為3m的a球置于地面上,質量為 m的b球從水平位置靜止釋放.當a球對地面壓力剛好為零時,b球擺過的角度為θ.下列結論正確的是

(A)θ=90°.

(B)θ=45°.

(C)b球擺動到最低點的過程中,重力對小球做功的功率先增大后減小.

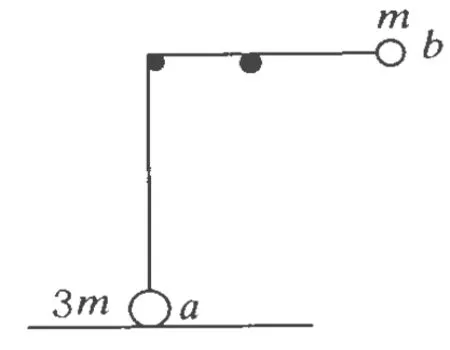
圖3

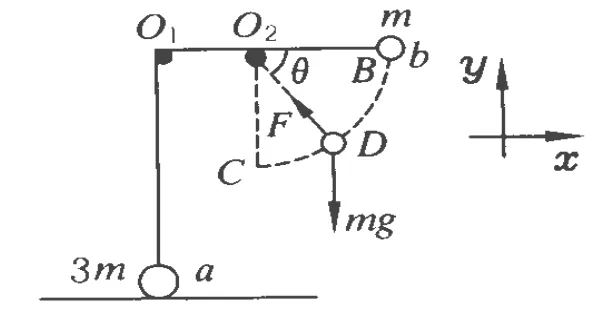
圖4

(D)b球擺動到最低點的過程中,重力對小球做功的功率一直增大.解析:本題要解決的是兩個問題,一是b球運動到何處,繩子上的拉力恰為3 mg?第2個問題其實只要討論b球運動過程中豎直方向的速度如何變化?對于第1個問題結合機械能守恒定律和牛頓第二定律不難得出,當θ=90°時繩子上的拉力為3 mg,此時a球對地面壓力剛好為零,現在重點來研究第2個問題.重力做功的(瞬時)功率可表示為 P=mgvy,其中 vy為豎直方向的分速度,要判斷重力的功率如何變化,只要判斷 vy如何變化.從兩個極端位置不難做出定性判斷,在B點v=0,vy=0,P=0;到C點速度水平,vy=0,P=0.因此可以確定,重力對小球做功的功率先增大后減小.現在的問題是物體擺動90°過程中vy的極值點唯一嗎?如何確定b球擺動90°過程何處最大呢?

通常的討論方法是根據B→D過程機械能守恒得出D點的速度,然后求其豎直分速度,得到vy與θ的函數關系,最后,計算 vy的極值,這種方法得到的 vy與θ的函數關系與例1中(1)式有同樣的形式,此處不具體展開.

現在,我們從動力學角度來求解這一運動學極值問題,如圖4所示,b球繞O2擺過θ角度到達D點,速度為v,繩子上拉力為F,對于這一過程,由機械能守恒定律得

式中 l為O2B繩子的長度,在D點,由牛頓第二定律得

解(2)、(3)式得

可見,物體擺動 90°過程中,當 θ由0°變化到35°的過程中逐漸增大,當 θ由35°變化到 90°的過程中逐漸減小.在當θ=35°時有唯一的極大值點.

所以,本道題的正確選項為(A)、(C).

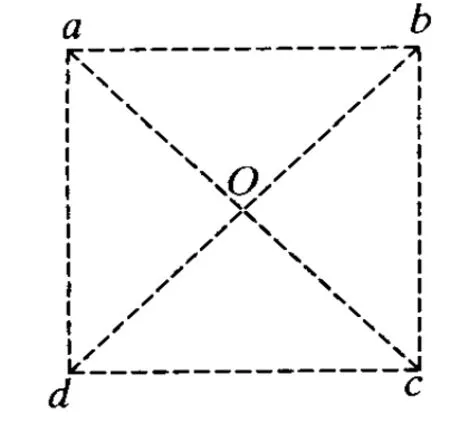
圖5

例3.(2009年安徽高考理綜題)在光滑的絕緣水平面上,有一個正方形 abcd,頂點 a、c分別固定一個正點電荷,電荷量相等,如圖5所示.若將一個帶負電的粒子置于 b點,自由釋放,粒子將沿著對角線bd往復運動.粒子從b點運動到d點的過程中

(A)先做勻加速運動,后做勻減速運動.

(B)先從高電勢到低電勢,后從低電勢到高電勢.

(C)電勢能與機械能之和先增大,后減小 .

(D)電勢能先減小,后增大.

解析:本題以一對等量同種電荷的電場為背景,研究帶電粒子在電場中的運動,綜合考查牛頓定律、功和能的關系,其中,選項(A)的錯誤是顯然的,因為這是一非勻強電場,粒子的運動一定是變加速的,即不會是勻加速或勻減速運動.在ac的垂直平分線上,O點場強為零,電勢為最高,負電荷在O點電勢能為最小,粒子運動過程中受到的電場力始終指向O點,即粒子從 b點運動到d點的過程中,電場力先做正功后做負功,電勢能先減小后增大,機械能則先增大后減小.電勢能與機械能的總和保持不變.可見,本題的正確選項為(D).

現在要借題發揮的是,帶電粒子從b點運動到d點的過程中加速度如何變化?

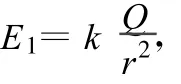
顯然(5)式與例1中(1)式是相同的形式,有著同樣的極值解.作為一種數學方法,我們通過微積分知識再來研究一下這個函數的極值.

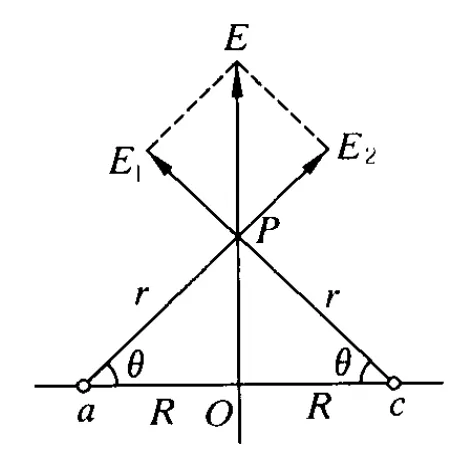
圖6

(5)式中場強E為θ的函數,將E對θ求一階導數和二階導數來討論極值點.

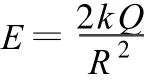
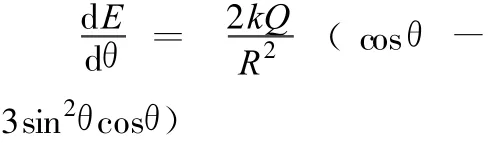
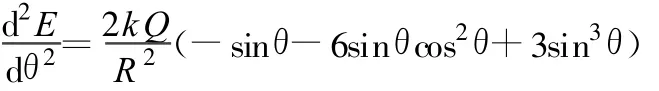
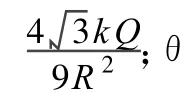
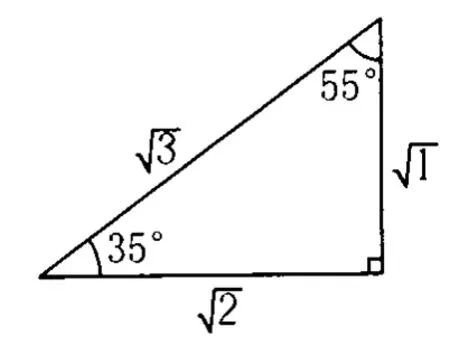
圖7

根據以上分析可知,本道高考題中帶負電的粒子從b點運動到O點的過程中加速度是先增大到某一極大值后逐漸減小到零,粒子從O點運動到d點的過程中加速度是先從零開始增大到某一極大值后逐漸減小.

在本文以上討論的問題中,雖然物理背景各不相同,但卻有著共同的解:即臨界角θ=35°(或θ=55°),聯系著同一個直角三角形,如圖7所示.相信一定還會在其他的物理問題中出現這樣的特殊角,讓我們記住這樣的一個來自于真實物理背景的特殊角吧.