某V型發動機曲軸結構強度有限元分析及方案比較

陳 偉，溫世杰，彭海雄

（中國北方發動機研究所，山西大同037036）

曲軸是發動機中最重要的零件之一，承受著氣缸內氣體壓力以及往復和旋轉質量慣性力引起的周期性變化載荷。曲軸內產生交變的彎曲應力和扭轉應力，可能引起曲軸的疲勞失效，甚至斷裂。如何比較準確的得出曲軸應力大小以及分布，對于指導曲軸的設計和結構改進，具有很重要的意義。

本文所做的工作，是使用有限元分析法對某V型發動機曲軸的兩種結構方案（簡稱A方案、B方案）在爆發工況載荷作用下進行應力數值模擬，對其強度計算結果進行分析，為曲軸結構設計提供理論依據。

1 三維模型的建立

曲軸各單拐的結構及所受載荷是相同的。計算模型采用3個完整的單拐，選取中間拐為爆發載荷施加位置，以中間拐為計算考察對象。按照圖紙實際尺寸值，應用Pro／E軟件建立曲軸結構三維實體模型如圖1所示。曲軸B方案與A方案相比較，連桿軸頸增加5 mm，曲柄臂寬度增加20mm，弧度半徑增加6mm。

圖1 曲軸結構三維實體模型

2 有限元模型的建立

由于曲軸結構形狀的復雜性、載荷的交變性，局部存在較高應力，在對曲軸進行有限元分析時，需要根據曲軸的結構特點、載荷性質以及分析目的選擇適當的計算模型。

2.1 結構離散

將計算模型劃分成曲軸區和支撐區兩部分。各部分材料物理特性參數見表1所列［1］。

表1 各部分材料物理特性參數

為了提高有限元模型的計算精度及控制整個有限元模型的計算規模，對模型各部分設定了不同的單元長度。將主軸頸過渡圓角處、曲柄銷過渡圓角處以及油孔周圍網格進行細化，這樣可提高這些區域的計算精度，力求準確地反映出這些區域的應力集中情況。

有限元模型曲軸實體部分，采用10節點四面體單元，軸承座因形狀規則，采用六面體單元。曲軸有限元計算網格模型如圖2所示。

圖2 曲軸有限元計算網格模型

2.2 位移和載荷邊界條件

根據曲軸的實際工作情況，在有限元模型中施加相應的位移約束邊界條件和載荷邊界條件。

發動機連桿受力曲線如圖3所示。

按照中間拐爆發時，由曲柄連桿機構運動學計算出相鄰各氣缸的曲軸受力。在各拐的連桿軸頸上施加曲軸切向力和徑向力。曲軸位移和載荷邊界條件施加狀態如圖4所示。

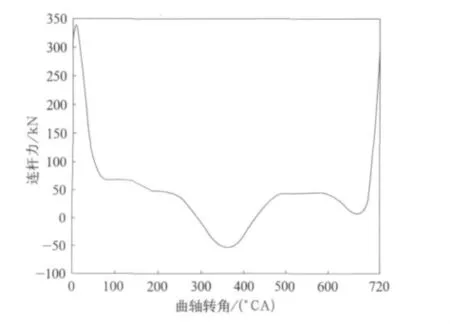
圖3 發動機連桿受力曲線

圖4 曲軸位移和載荷邊界條件施加狀態

2.3 接觸邊界條件

對于由曲軸、主軸承座組成的組合結構，裝配接合面上有接觸關系，計算時程序根據接觸狀態通過接觸面上建立的接觸單元自動完成作用力的傳遞，完成接觸模擬。

3 計算結果及分析

曲軸結構具體考察區域如圖5所示。其中，1、6區為主軸頸過渡圓角區域，2、5區為曲柄銷過渡圓角區域，3、4區為連桿軸頸油孔部位。各個區域均考察了最大主應力、最小主應力和等效應力。

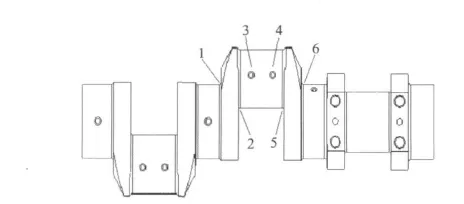
圖5 曲軸結構具體考察區域

3.1 曲軸A方案具體考察區域應力值如表2所示。

3.2 曲軸B方案具體考察區域應力值如表3所示。

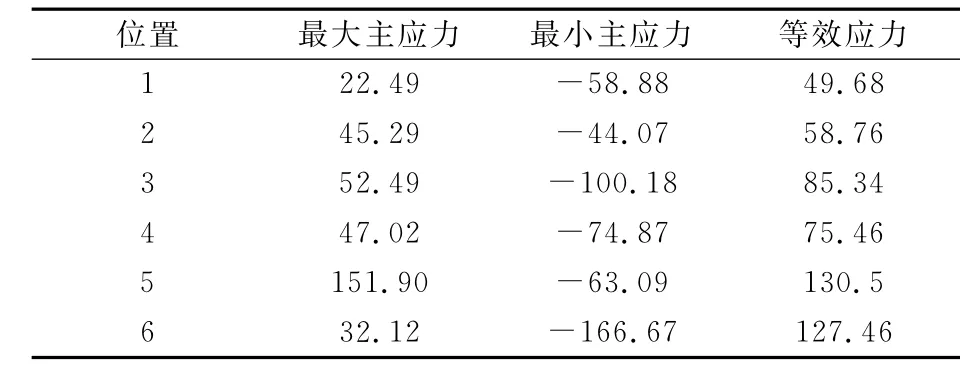
表2 曲軸A方案具體考察區域應力值MPa

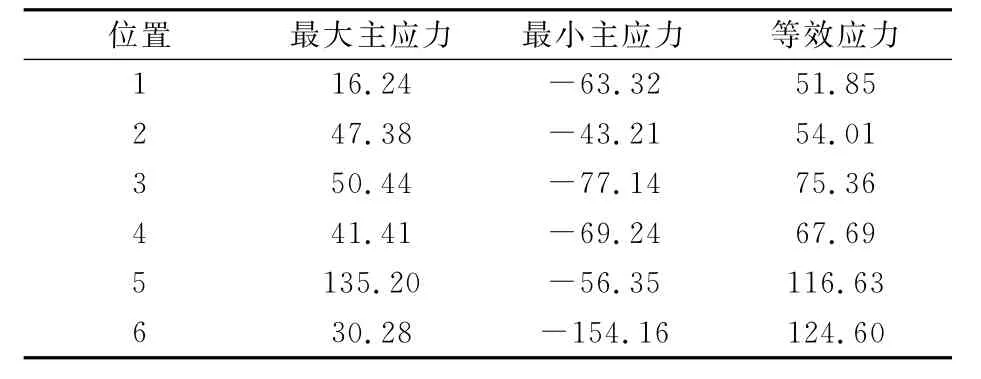
表3 曲軸B方案具體考察區域應力值 MPa

3.3 靜態安全系數

曲軸采用42CrMoA材料，其屈服極限和強度極限分別為930MPa、1 080MPa［2］，從列表中看到計算所得的等效應力、最大主應力、最小主應力的值均遠小于材料的屈服極限和強度極限，按照第一強度理論，曲軸A方案和B方案在靜載下的安全系數分別達到6.12和6.88。按照第四強度理論，曲軸A方案和B方案在靜載下的安全系數分別達到7.13和7.46。

3.4 疲勞強度安全系數

曲軸單拐平均應力和應力幅最大的部位出現在連桿軸頸下部與曲柄臂夾角處，選取此部位做為疲勞安全系數計算的區域。

非對稱循環的彎曲疲勞安全系數可通過式（1）計算［3－4］：

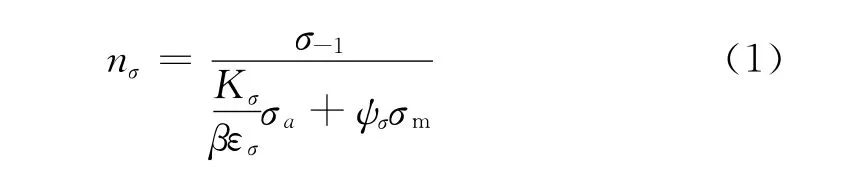
式中σ－1為材料對稱循環彎曲疲勞極限，σ－1＝0.45 σb

［4］；σa為應力幅；σm為平均應力；Kσ為彎曲時圓角處的應力集中系數，取1.0；β為強化系數，所分析的曲軸沒有采用圓角強化工藝措施，故取β＝1.0［4］；εσ為絕對尺寸影響系數，在文獻［4］中查得為0.62；ψσ為材料對應力循環不對稱的敏感系數，按式（2）進行計算［4］。

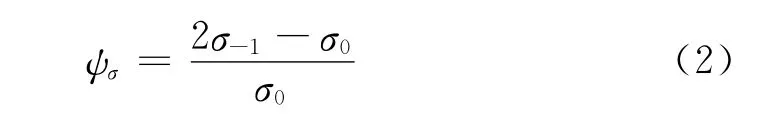
其中σ0為脈動循環時材料的彎曲疲勞極限，取σ0＝（1.4～1.6）σ－1［4］。

通過計算，曲軸A方案和B方案的疲勞強度安全系數分別為2.58和2.90。

4 結論

（1）曲軸A方案和B方案，其靜強度滿足可靠性要求。

（2）由文獻［4］，曲軸規定的疲勞安全系數為1.5～2.0，曲軸A方案和B方案的疲勞強度滿足可靠性要求。

（3）通過對比曲軸A方案和B方案的計算結果，可以得出，曲軸B方案其靜強度、疲勞強度比A方案都有明顯提高，曲軸B方案設計要優于A方案設計。

［1］朱張校.工程材料［M］.北京：清華大學出版社，2001.

［2］聞邦椿.機械設計手冊［M］.北京：機械工業出版社，2010.

［3］劉鴻文.材料力學［M］.北京：高等教育出版社，2000.

［4］楊連生.內燃機設計［M］.北京：中國農業機械出版社，1984.