讓學生在實例的體驗中生成
226001 江蘇省南通市第一初級中學 劉 寧
讓學生在實例的體驗中生成
226001 江蘇省南通市第一初級中學 劉 寧
“函數”可以說是整個初中數學中最抽象、最復雜的一個概念.如何通過具有函數關系的實際問題,讓學生在經歷和體驗變量與函數產生的過程中,建立函數基本概念,激發學生學習興趣,培養學生歸納問題、分析問題、解決問題的能力,是我們一直探索的問題,本文結合筆者參加南通市區青年教師優課評比(一等獎)的一節課來說明.
1 創設情境,導入新課
師:當我們向平靜的湖面扔一塊石子,湖面會發生怎樣的變化?(給出兩幅圖片:近處是平靜的湖面和綠洲,遠處是雪山)
生:“水面會產生波紋”、“水面會出現許多圓”、“以石子落入點為中心向四周蕩漾開去”……(你一言我一語)
師:登山運動員登山,隨著海拔的升高,氣溫會怎樣變化?
生(異口同聲):降低.
點評 此時同學們的情緒異常高漲,都想知道這些變化著的物體之間有著怎樣的聯系,這兩個問題激發起了學生的求知欲望,使他們的注意力迅速集中到課堂.
2 自主探究,形成概念
學生小組合作,完成下述三個問題:
問題1 每張電影票的售價為10元.
(1)若一場售出150張電影票,則該場的票房收入是______元;若售出205張、310張呢?
(2)若一場售出x張電影票,則該場的票房收入y元,則y = ______.
問題2 在一根彈簧的下端懸掛重物.如果彈簧原長10cm,每1kg重物使彈簧伸長0.5cm.
(1)根據題意填表;

m(kg) 0 1 2 3 4…l(cm)10
(2)設重物質量為mkg,受力后的彈簧長度為lcm,則l = _______.
問題3 圖1是南通冬季某一天的氣溫T隨時間t變化的圖象,看圖回答:
(1)這天的8時的氣溫是_______℃,14時的氣溫是_______℃;
(2)這天的最高氣溫是________℃,最低氣溫是________℃;
(3)這一天中,在4時 ~12時,氣溫( ),在16時~24時,氣溫( ).
A.持續升高 B.持續降低 C.持續不變

圖1
師:上述三個問題中,分別涉及到了哪些量?
根據學生的回答,教師板書:
問題1 票房收入y 售出票數x 單價
問題2 彈簧長度l 重物質量m 每1kg重物彈簧伸長長度 彈簧原長
問題3 氣溫T 時間t
師:上述三個變化過程中出現的這些量有什么特征?
生:有些量的數值發生變化,有些量的數值是始終不變的.
師:你能給這樣的兩種量取個名稱嗎?
生:變量,常量.
師:請同學們也來提一些反映不同事物變化過程的問題,讓大家尋找其中的變量與常量.
教師小結變量和常量的概念
點評 通過學生的自主活動,定義出兩個概念,讓學生初步體會到了成功的喜悅,更充滿信心地投入到下一環節的學習中.
師:這些變量之間存在著怎樣的關系?
生:一個變量隨另一個變量的變化而變化.
根據學生的回答,教師補充板書:
問題1 票房收入y 售出票數x 單價10元
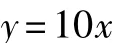
問題2 彈簧長度l 重物質量m 每1kg重物彈簧伸長長度0.5cm 彈簧原長10cm

問題3 氣溫T 時間t
氣溫T隨時間t的變化而變化.
師:兩個變量的值之間是如何變化的?
生:一個變量的值確定了,另一個變量的值也唯一確定了.
師(追問):上述三個問題中哪個變量的值確定了,另一個變量的值就唯一確定?
小組討論:發現在問題三中,時間t確定,溫度T就唯一確定;但溫度T唯一確定,時間t并不是唯一確定的.
問題1 票房收入y 售出票數x 單價
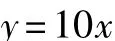

氣溫T隨時間t的變化而變化.
教師對學生的回答給予肯定,并再次強調:上述三個問題都研究了兩個變量之間的關系.它們都存在“在一個變化過程中,如果有兩個變量x與y,并且對于x的每一個確定的值,y都有唯一確定的值與其對應”這一共性.在此基礎上,給出函數的概念.
點評 通過對三個實例的進一步研究和問題的解決,函數概念的定義幾乎是水到渠成.同時,讓學生舉出身邊的實例并運用新知識建模,加深了他們對函數概念的理解.同時讓他們感到數學就在身邊,從而增強了對函數的體驗.
3 基礎訓練,鞏固新知
1.汽車由南通駛往相距500公里外的杭州,它的平均速度是100公里/小時,則汽車距杭州的距離s(公里)與行駛時間t(小時)的函數關系式?

t(小時) 1 2 3 …t s(公里)
(1)s隨t變化的關系式s=_______,______是自變量,________是________的函數;
(2)當行駛時間為3.5小時,s為________公里.
2.周末,小李8時騎自行車從家里出發,到野外郊游,16時回到家里.他離開家后的距離s(千米)與時間t(時)的關系如圖2所示.
(1)當 t=12時,s=________;當 t=14時,s=_______;
(2)小李從________時開始第一次休息,休息時間為_______小時,此時離家_______千米.
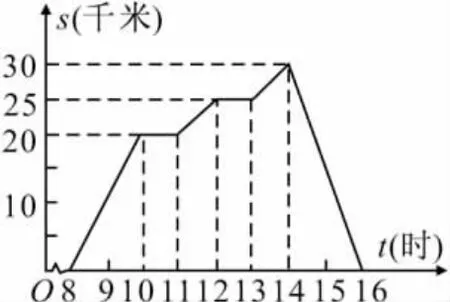
圖2
(3)距離s是時間t的函數嗎?時間t是距離s的函數嗎?
點評 圖表體驗培養了數形結合的思想,函數不再抽象.
4 總結歸納,深化新知
師:“回想一下本節課開始的兩個圖,我們能否將其中變量之間的關系看成函數?”
生:圓的周長、面積都是半徑的函數;氣溫是高度的函數…
點評 圖函數與生活如此貼近,與本課的開始部分相呼應.
20111129)

