一元二次方程整數根問題解題探析
435241 湖北省陽新縣白沙中學 董才強
一元二次方程整數根問題解題探析
435241 湖北省陽新縣白沙中學 董才強
含有字母參數的一元二次方程的整數根問題是一種常見的題型,但這類問題涉及的知識點較多,思維的要求較高,所以難度比較大,學生往往望而卻步.本文通過一道中考試題來說明這類問題常用的幾種解法.
原題 (2011年黃石)已知二次函數y=x2-2mx+4m-8.
(1)當x≤2時,函數值y隨x的增大而減小,求m的取值范圍;
(2)以拋物線y=x2-2mx+4m-8的頂點A為一個頂點作該拋物線的內接正三角形AMN(M,N兩點在拋物線上),請問:△AMN的面積是與m無關的定值嗎?若是,請求出這個定值;若不是,請說明理由.
(3)若拋物線y=x2-2mx+4m-8與x軸交點的橫坐標均為整數,求整數m的值.
解 (1)二次函數y=x2-2mx+4m-8的圖象是開口向上,對稱軸為直線x=m的拋物線,
∵當x≤2時,函數值y隨x的增大而減小,
∴ m≥2.
(2)如圖1所示,設拋物線的對稱軸與MN交于點B,根據拋物線和正三角形的對稱性可知:MN∥x軸,且AB垂直平分MN.
設 M(a,b),則點 B 的坐標為(m,b),顯然有 m>a,
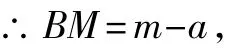
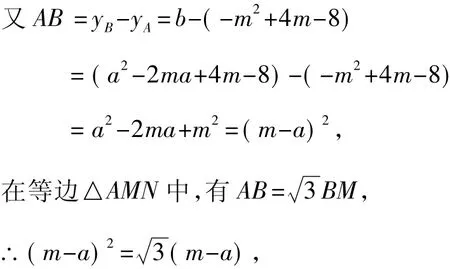
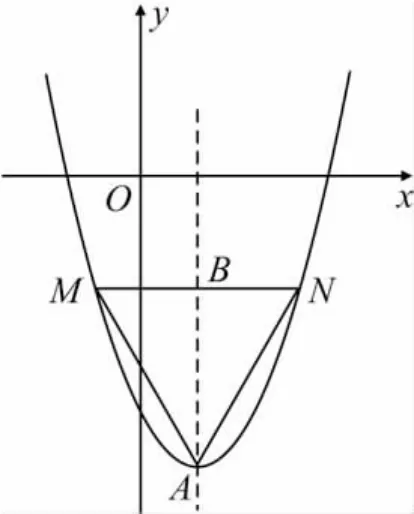
圖1
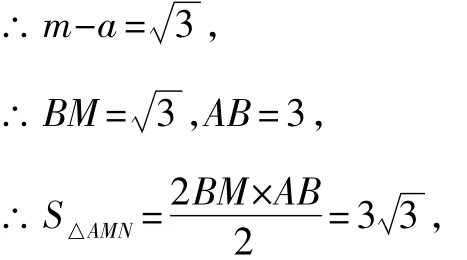
即△AMN的面積是與m無關的定值.
(3)很明顯,這一問的本質是一個含有字母參數的一元二次方程的整數根問題,下面對第(3)問的解法作重點探討.
解法1 利用判別式
令y=0,即可得到關于x的一元二次方程:
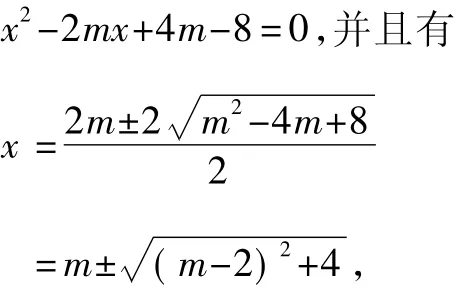
由題意,(m-2)2+4必須為完全平方數,不妨設(m-2)2+4=n2(其中n為整數),
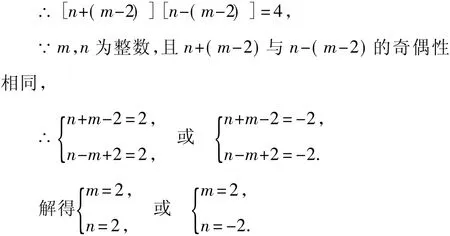
經檢驗,當m=2時,關于x的一元二次方程x2-2mx+4m-8=0有整數根,∴m=2.
點評 本題解法的最后一步檢驗雖一語帶過,但卻是一個必不可少的步驟.因為整系數一元二次方程的判別式是完全平方數只是該方程有整數根的必要條件,但不是充分條件.也就是說,當△為完全平方數時,并不能保證方程一定有整數根,所以必須進行檢驗.
解法2 利用因式分解
對方程x2-2mx+4m-8=0稍作變形:

∴當方程有整數根時,x=4或0,這時m=2.
點評 這個解法只用到整式的變形(先配方,再因式分解),解題的必要性和充分性同時實現,參數和未知數的值也同時求出,而且不需要代入檢驗,減少了出錯的機會.
解法3 利用根與系數的關系
∴當方程有整數根時,m=2.
點評 這個解法沒有用到“m為整數”的條件,更反映出本題的特殊結構,并且對學生來說,比上述各解法更容易想到.
解法4 構造恒等式

點評 這個解法同解法3形式上很相似,只是消去參數m的途徑略有差異.而且,由于恒等式中的x可以任意取值,能為我們用于各種場合提供方便.同解法3一樣,由于本題要求參數m為整數,所以必須對求出的x1,x2進行取舍.
解法5 變換主元,反客為主

點評 這個解法變換了思維角度,視m為主元x為參數,則易于求出m,再利用代數式的恒等變形和整除的性質來達到求解的目的.
由此可見:解答含有參數的一元二次方程的整數根的問題雖然技巧性強,但是有規律可循,要仔細觀察所給方程的特征,綜合運用所學知識,選擇簡便的解法.
20110925)

