鐘面上的數學問題

733000 甘肅省武威第十三中學 張曉輝

鐘面上的數學問題

733000 甘肅省武威第十三中學 張曉輝

鐘面行程問題是研究鐘面上的時針和分針關系的問題.在鐘面上每針都沿順時針方向轉動，但因速度不同總是分針追趕時針，或是分針超越時針的局面，因此常見的鐘面問題往往轉化為追及問題或相遇問題來解決.

1 時針與分針的重合問題——可轉化為追及問題解決

鐘面上除了12點到1點這一時段里分針一開始就領先時針跑在前面不會與時針重合外，其它時段，分針總能在某一時刻追上時針并與時針正好重合.這樣，就形成了一個有趣的數學問題：時針與分針究竟在幾時幾分重合?

我們就可以將此題理解成跑得快的分針在后面追跑得慢的時針，這樣，時針與分針的重合問題就轉化成了追擊問題.

問題1 3時多少分時，時針與分針重合?

分析 這個問題實際上就是行程問題中的追及問題，3時分針指著12，時針指著3，分針與時針相距5×3=15小格(90°).分針每分鐘走 1 小格(6°)，時針每分鐘走小格(0.5°).要使分針與時針重合，分針要比時針多走15小格(90°).根據追及問題中的速度差×追及時間=路程差列式即可.

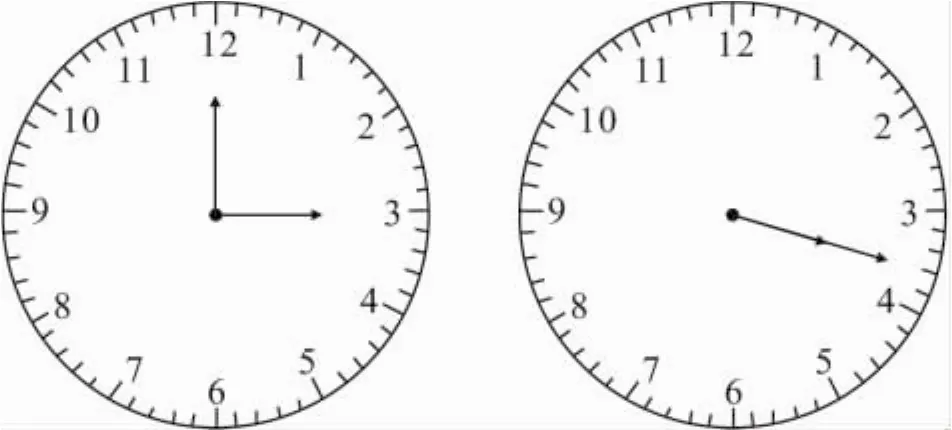
圖1

解 設分針到x分時，時針與分針重合.

根據題意，得

問題2 一晝夜時針和分針能重合多少次?

解析 如果我們把零點看作是重合的，那么12點、24點就不算重合，否則就重復計數了.這樣答案就很清楚了：從1點開始的每一整點開始，到下一整點，都是分針追趕時針，并且在一定的時刻一定會相遇.24小時內，時針和分針重合22次，既不是24次，也不是23次.你可以轉動一只手表來檢驗一下.

方法總結

2 時針與分針的對稱問題——可轉化為相遇問題解決

時針與分針正好處在某一數字的兩邊，并且與這一數字所在軸線形成的夾角相等，我們就說：此時時針與分針關于某一數字對稱.

顯然，對稱問題中時針與分針的位置關系與重合問題不完全相同，重合問題中分針追到了時針，而對稱問題中分針并沒有追到時針.如果仍用重合問題的解題思路，本題無法解決.怎么辦?認真觀察鐘面，我們會發現，分針與時針關于某一數字對稱的情形，都是分針從數字12出發，追到快接近這個數字的時候，此時，分針離表示整點的數字有多遠，時針就正好離開這個數字有多遠，如果時針倒過來行走相同時間，就正好與分針在分針現在所在的這一位置相遇.這樣，時針與分針的重合問題就轉化成了相遇問題.

問題3 5點過多少分時，時針和分針離“5”字的距離相等，并且在“5”的兩邊?

分析 假設5點以后，時針以相反的方向行走，時針和分針相遇的時刻就是本題所求的時刻.這就變成了相遇問題，兩針所行距離和是25小格(150°).

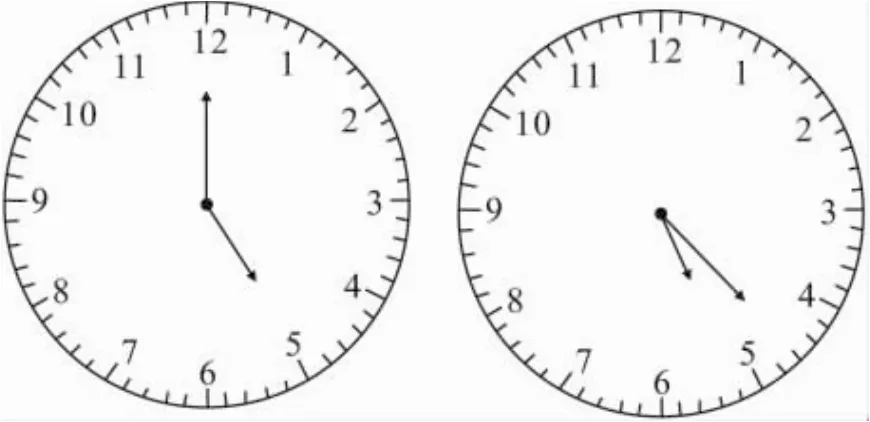
圖2

解 設經過x分時，時針和分針離“5”字的距離相等，并且在“5”的兩邊.

根據題意，得

方法總結

3 時針與分針的夾角問題——分多種情況綜合考慮

鐘面上時針與分針不停地走動，它們之間的關系也在不停地在變化，就會出現重合，銳角，直角，鈍角，平角等情況.于是，就出現了下列幾種求角度的趣題：

3.1 求某一時刻時針與分針夾角的度數

問題4 9時35分，時針與分針的夾角是多少度?

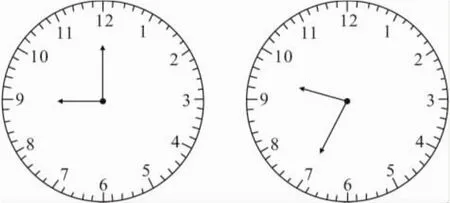
圖3

分析 我們可以將9時作為初始位置，9時35分時，分針指向7，分針經過了35小格，時針走了35分鐘，走了×35格，分針走的格數加上時針與分針的夾角的格數，正好等于9對應的格數加上時針35分鐘走的格數.

解 設9時35分，時針與分針的夾角是x度.

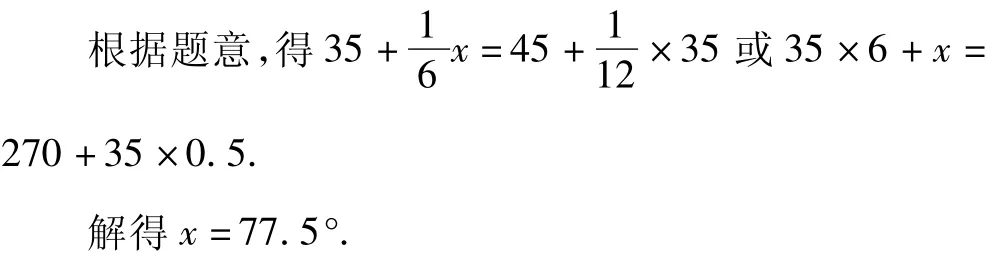
答：9時35分，時針與分針的夾角是77.5°.

方法總結

一般地，時針與分針在某一時刻m時n分的夾角x，

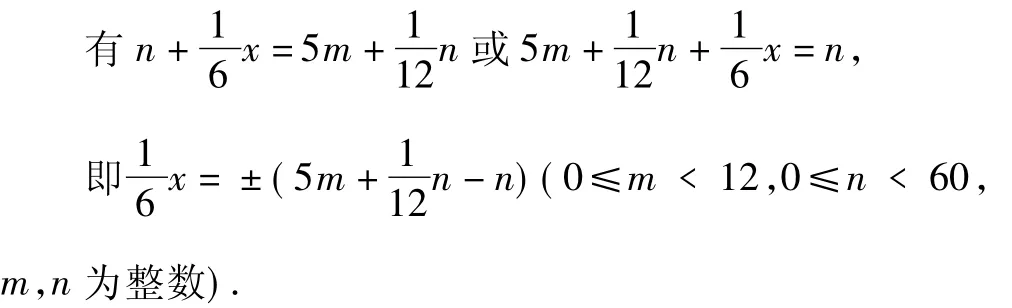
3.2 求時針與分針何時成直角

問題5 在7點與8點之間，時針與分針在什么時刻相互垂直?

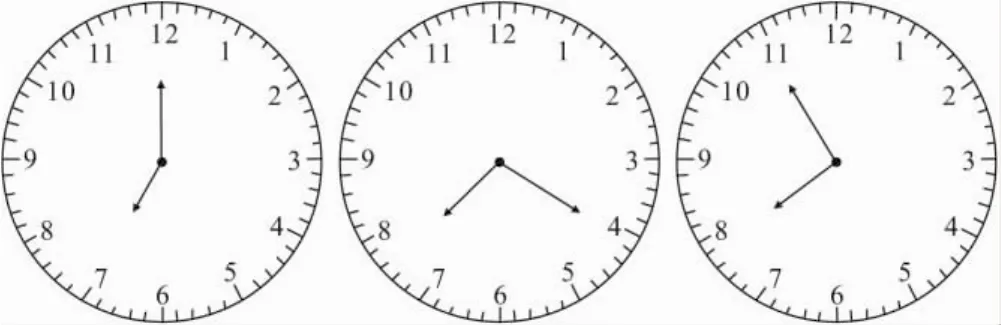
圖4

分析 7點時分針指向12，時針指向7，分針在時針后面5×7=35(格).時針與分針垂直，即時針與分針相差15格，在7點與8點之間，有兩種情況：

(1)分針在時針后面15格.從7點開始，分針要比時針多走35-15=20(格).

解 設從7點開始，經過 x分，時針與分針相互垂直.

根據題意，得

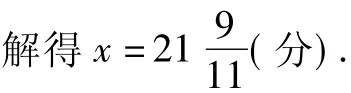
(2)分針在時針前面15格.從7點開始，分針要比時針多走35+15=50(格).

根據題意，得

問題6 時針與分針在11點幾分時相互垂直?

分析 11點時，時針在分針前11×5=55格，時針與分針要相互垂直，分針須在時針后15格或45格.從11點開始，分針要比時針多走55-15=40(格)，或55-45=10(格).

解 設時針和分針在11點x分時相互垂直.

根據題意，得

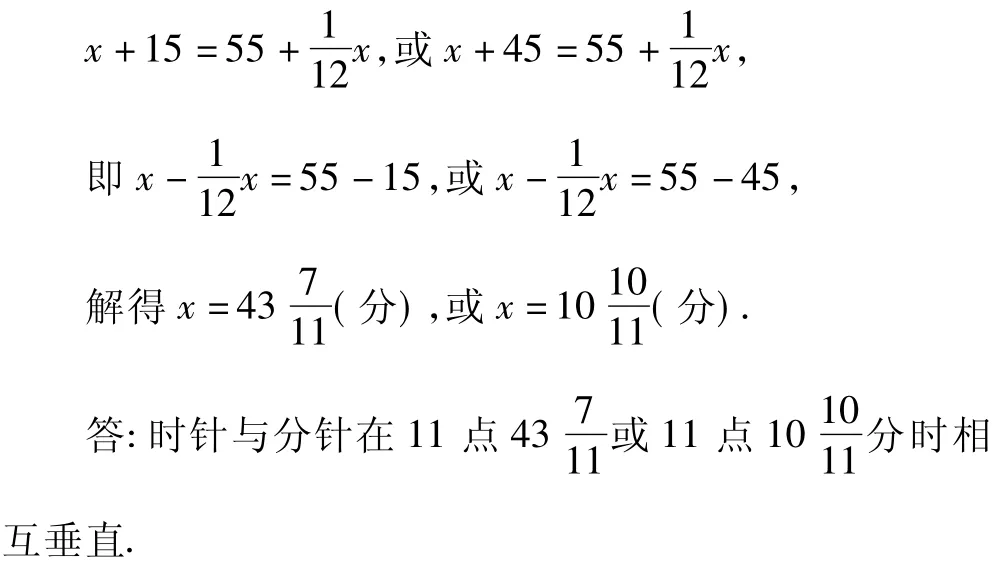
方法總結

一般地，時針與分針在m時x分成直角(m是整數).

3.3 求時針與分針何時成平角

問題7 在3點與4點之間，時針和分針在什么時候反向成一直線?

分析 3點時分針指向12，時針指向3，分針在時針后面5×3=15(格).時針與分針反向成一直線，即時針與分針成180°角.從3點開始，分針要比時針多走15+30=45(格).

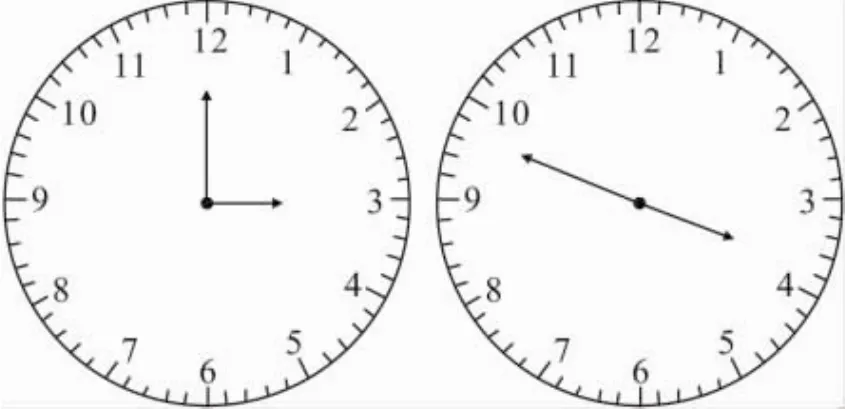
圖5

解 設從7點開始，經過x分，時針與分針反向成一直線.

根據題意，得

問題8 時針和分針在10點幾分反向成一直線?

分析 10點時，時針在分針前50格，時針和分針反向，時針須在分針前30格.從10點開始，分針要比時針多走50-30=20小格.

解 設10點x分時針和分針反向，

根據題意，得

方法總結

一般地，時針與分針在m時x分在一條直線上，若6點以前：x-x=5m+30(0≤m＜6，m為整數)，若6點以后為整數).

20110715)