話(huà)說(shuō)不等式x1x2＜0

九頭鳥(niǎo)茶樓常客 萬(wàn)爾遐

話(huà)說(shuō)不等式x1x2＜0

九頭鳥(niǎo)茶樓常客 萬(wàn)爾遐

1 高中教師的賽題

以下的這道賽題，本來(lái)是用來(lái)考高中教師的：

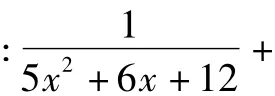
問(wèn)他怎么得到的，他說(shuō)是猜到的!高中教師說(shuō)他是胡猜，而初中教師說(shuō)他是妙猜!

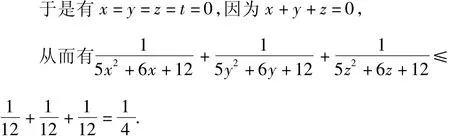
高中教師說(shuō)：這不算解答，這還是猜想!

初中教師說(shuō)：這不是猜想，這是證明!

高中教師說(shuō)：這是什么證明，這只能說(shuō)是“公理”!

初中教師說(shuō)：哦，“公理”不行，那么“私理”何在?

于是高中教師拿出了一個(gè)“私理”解法，由于“私”得過(guò)分，成了許多高中師生都看不懂的“高解”.

……

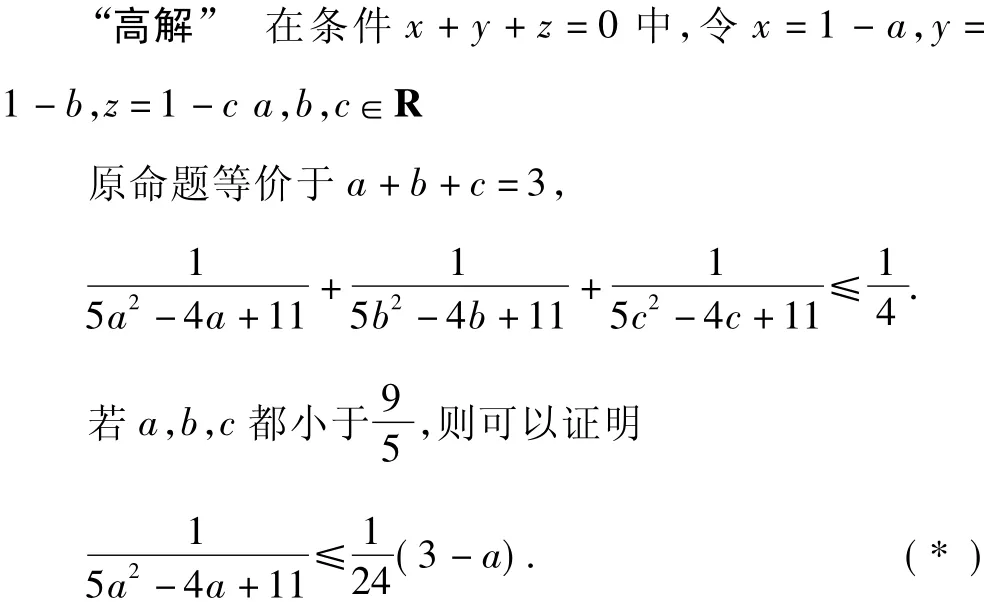
質(zhì)疑 初中教師插話(huà)：你那個(gè)“可以證明”，我還沒(méi)有看懂.但有一點(diǎn)我已經(jīng)看到，這種解法是個(gè)舍近求遠(yuǎn)的迂解!

x+y+z=0也好，a+b+c=3也好，無(wú)非是“三數(shù)之和為常數(shù)”!至于“常數(shù)”，我以為，常數(shù)0比常數(shù)3簡(jiǎn)單!

2 初中教師的解法

3 拿著x1x2＜0破題

當(dāng)且僅當(dāng)x=y=z=0時(shí)，有最大的常數(shù)λ=3.

x1x2＜0解法 由a+b+c=3得a-1+b-1+c-1=0.

令 a-1=x，b-1=y，c-1=z，

則 x+y+z=0，a=x+1，b=y+1，c=z+1.

原問(wèn)題化為前面的那道賽題：

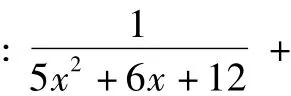
4 拿著x1x2＜0當(dāng)牛刀

為展示x1x2＜0的能耐，以下把x1x2＜0當(dāng)牛刀使用!

題目 試求最小的常數(shù)λ，使得下列不等式對(duì)于滿(mǎn)足條件x+y+z=0的實(shí)數(shù)x，y，z恒成立：

當(dāng)且僅當(dāng)x=y=z=0時(shí)，有最小的常數(shù)λ=36.

余興 哈哈!這個(gè)題目還用得著牛刀x1x2＜0出場(chǎng)嗎?

嘻嘻!正是要在雞群面前顯示牛刀x1x2＜0的威風(fēng)!

20110829)