地區統計數據準確性質量的比較

龔敏慶，孫明偉，金明仲

（1.貴州民族學院，貴陽 550025；2.貴州大學,貴陽 550025）

0 引言

Behrens[1]-Fisher[2]（B-F）問題在統計理論與應用中具有重要作用，若兩個正態總體的協方差陣未知且不同，根據樣本來檢驗兩總體均值相等的檢驗的問題稱為B-F問題。對于求解單變量B-F問題，Scheffe[3]提出了一種將初始的二樣本問題轉換為單總體問題的轉換方法，以便通過傳統的t-檢驗方法進行檢驗。Welch[4]在研究學生t-分布的基礎上提出了一種近似自由度法。Bennett[5]擴展了Scheffe[3]的轉換方法，用于求解多元B-F問題。Anderson[6]指出這種轉換方法的優點是在檢驗過程中用到的樣本均值向量的差異與總體均值向量差異密切相關。Welch[4]的近似自由度方法也被擴展到多元B-F問題方面。ZHANG JinTing和XU JinFeng[7]研究了高維多總體B-F問題，他們也擴展了Scheffe的變換方法，提出利用L2-檢驗方法于Hotelling的T2-檢驗方法無法使用一些場合，那是一些檢驗多個具有不同協方差陣的高維正態總體的均值向量是否相等的場合。

質量優良的地區統計數據，是政府制訂正確方針、政策，診斷宏觀經濟運行好壞的有效參考，因此我國對于提高地區統計數據質量的研究和實踐十分重視。對統計數據質量的研究各國和一些國際組織構建了不同的數據質量評價和管理體系。文獻[8]構建了地區統計數據質量準確性方面的B-F問題，針對我國部分地區的統計數據，通過對時間序列數據的擬合建模，討論其準確性，檢驗各個地區統計數據質量準確性是否存在顯著性差異。本文是文獻[8]研究的繼續，在文獻[8]的基礎上對各個地區的統計數據質量的準確性差異進行評估和分析，創新要點在于對不同地區統計數據質量的準確性進行排序比較的方法，這也是討論地區數據質量準確度可比性的一個方面。該方法也可以考慮用于統計數據質量的其他方面，使得我們可以從統計數據質量的八個方面構建統計數據質量的評估比較系統。

1 擴展Scheffe轉換法[7]

我們可以用擴展Scheffe轉換方法[3][7]，將多總體B-F問題轉換為單總體問題。單總體問題分布為：

這里Nq(μ,Σ)表示均值向量為μ，協方差陣為Σ的q維正態分布。設q的值較大，μ和Σ未知。單總體問題檢驗假設為：

這里μ0是已知q維向量。

考慮多總體B-F問題：假設有k個獨立正態總體，對于l=1,2,...,k:

Np(μl,Σl)是均值向量為μl，協方差陣為 Σl的p維正態分布。多總體B-F問題檢驗k個均值向量是否相等：

這里不假定協方差陣Σl(l=1,2,…,k)相等。

用以上Scheffe[3]方法，把后面的k-1個樣本轉換為單總體樣本得到：

A?B為矩陣直積，Jk-1為所有元素均為1的(k-1)階方陣，diag(A1,A2,…,Al)表示對角線分塊矩陣分別為A1,A2,…,Al的矩陣。這樣k總體B-F問題(3)的變量就轉換為正態總體(4)獨立同分布的單總體變量，從而可以利用單總體問題的檢驗方法。

由孫明偉等論文[14]可知：當q遠小于n1時，此問題可以用HotellingT2-檢驗方法。(4)的變量是獨立同正態分布的，其均值向量為：

這表明μ=0當且僅當μ1=μ2=…=μk，因此k總體B-F問題關于零假設（3）的檢驗轉化為單總體問題相應于零假設（2）的檢驗。μ的估計可為樣本均值向量：

2 地區統計數據質量評估方法

對于時間序列統計數據，可根據數據的變動規律構造模型，對序列的變化趨勢進行擬合，然后通過比較樣本觀察值與模型的預測值來評估統計數據質量。

對于非平穩的時間序列Xt，可以用Xt=f(t)+vt來描述，其中f(t)表示Xt隨時間變化的均值，為序列的確定性部分；vt為Xt殘差剩余部分。

質量良好的統計數據可以準確反應真實情況，并可以通過它們對未來的相應值進行有效的預測，將誤差控制在有效的范圍內。對統計數據準確性進行的定量分析利用統計指標的歷年數據的變化特點建模，并對模型進行一系列的統計檢驗，在模型通過各種檢驗、具有良好統計預測功能的基礎上，比較模型擬合出的預測值與實際觀察值，計算其偏離程度。以下介紹劉洪、黃燕（2007）論文中關于評估數據質量的方法之一：相對誤差法[12]。

用統計指標的當期實際值與根據模型計算出的預測值進行比較，計算出相對誤差ε，第n期的相對誤差為：

給定一個允許的誤差范圍，Xn表示實際觀察值，表示擬合估計值，如果 |εn|在該誤差范圍內，則可初步斷定統計指標的該期數據可靠，否則認為數據質量可能存在問題。允許誤差范圍的確定并沒有一個標準，不同的誤差范圍可能會得出不同的評估結果。

本文中我們將采用趨勢擬合評估法對所選的不同地區的經濟統計數據進行擬合，比較模型擬合出的預測值與實際觀察值，計算出其相對誤差的絕對值對其數據質量進行評估，并構建地區經濟統計數據質量的多總體B-F問題，討論相應的地區經濟統計數據質量準確性是否具有顯著性差異并進行排序比較。

3 實證研究

我們還是選取三個反映經濟發展情況的重要指標來對其數據質量進行評估，即地區生產總值(GDP)、全社會固定資產投資總額（FAI）和城鎮居民最終消費支出（FCE），并運用求解多總體B-F問題的方法對地區間部分有關經濟統計數據的數據質量進行檢驗，研究它們是否具有顯著性差異并對其質量準確性進行比較排序。

對于政府有關經濟方面的統計，大多用不變價格來計算發展速度。本文中選取地區自1999～2008年間相關指標的統計數據，但并未對其用不變價格換算系數進行換算，因為文中所構建的B-F問題是對地區間的統計數據質量是否有顯著性差異進行檢驗，并用觀察值與預測值間相對誤差的絕對值來反映數據質量的好壞，并沒有利用這些數據對地區間的經濟發展情況或是總產值的大小進行直接的比較，所計算出的結果都是相對值。因此，用現價對我們的問題并沒有影響。

我們對1999～2008年間關于三個省市，簡稱為B市、G省、和Y省分別選取上述相關指標的國家統計局公布的統計數據，這些數據均來自國家統計局所出版的《中國統計年鑒～2009》[9]，并運用趨勢擬合評估法對相關指標的趨勢進行擬合，利用擬合方程分別求出相應年份的擬合值，并計算其相對誤差的絕對值得到衡量其數據質量的指標數據，構建地區統計數據質量多總體B-F問題，分別比較三省市地區統計數據質量準確性是否存在顯著性差異并對其準確性質量進行排序對比檢驗。

對B市和Y省，用Matlab軟件對其時間序列地區統計數據作圖得圖1。由圖1可知，這三個指標序列與大多數的經濟序列一樣，是非平穩的，近似呈指數上升的趨勢，因此我們選擇指數模型來擬合上述三個指標的趨勢增長。

這里我們用Matlab軟件分別求出B市和Y省關于三個統計指標的實際觀察值與時間t之間的擬合方程后，再將相應的年份代入求得的方程，分別求出相應年份各指標的擬合值，并將擬合值與相應的實際觀察值代入公式(1),計算出該年份下相應指標的相對誤差，并取其絕對值，它們的大小反映了該地區相應年份對應統計數據質量的準確性。例如由圖1知B市1999～2008年間GDP隨時間t的增加呈指數增長，由Matlab得B市GDP的以下擬合公式：

然后將年份時間t分別代入上述方程求出B市該年的GDP擬合值，根據B市該年相應的GDP的實際觀察值G，將G與擬合值代入公式(6)，計算出相應的相對誤差值ε，并取其絕對值 ||ε，得到如表1的B市GDP相對誤差絕對值數據。用同樣的方法得到各地區關于相應的指標的擬合公式，計算出B市、Y省和G省這三個市省的地區生產總值(GDP)、全社會固定資產投資總額（FAI）、城鎮居民最終消費支出（FCE）等三個統計指標關于1999到2008年等年份相對誤差值的絕對值，由此得到表1。

然后可以用二總體B-F問題來討論，我們用上文中介紹的求解B-F問題的擴展Scheffe[3]轉換法，將此二總體問題轉換為單總體問題：

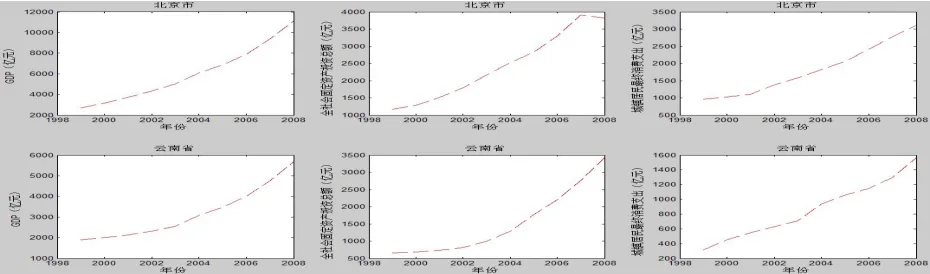
圖1 B市和Y省部分經濟統計數據

由以上數據得到μ和Σ，然后可以用二總體B-F問題來討論，我們用求解B-F問題的擴展Scheffe[3]轉換法，將此二總體問題轉換為單總體問題：

由以上數據得到μ和Σ的估計如下：

其樣本容量n=10，維數q=3。再用霍特林T2-檢驗方法對其進行均值向量檢驗：

取檢驗統計量：

經計算得：T2=20.1067

對于給定的顯著性水平α=0.05下，經Matlab軟件計算得其p值為（此時檢驗統計量F～F(3,7)：因p=0.0148＜0.05=α，故要拒絕H0，即不能接受B市和Y省的經濟統計數據質量準確性沒有顯著性差異的假設，兩者間存在顯著性差異。

進一步，我們對它們的統計數據質量準確性排序進行判斷和檢驗，這是本文的要點。為了對兩地區的三個經濟指標的準確性排序，分別進行判斷檢驗，我們提出比較其相對誤差絕對值的樣本均值大小的原假設

這里μ1、μ2分別表示B市和Y省的相應地區經濟指標統計數據相對誤差絕對值均值。

表1 1999～2008年三省市部分統計數據相對誤差絕對值

對于給定的顯著性水平α=0.05，利用Mat lab軟件進行計算，計算結果中引入參量[H,p]，H=0表示在顯著性水平α下，不能拒絕原假設，H=1表示在顯著性水平α下，可以拒絕原假設；p為當原假設為真時得到觀察值的概率，當p為小概率時則對原假設提出質疑。

原假設為B市地區統計數據質量優于Y省，即B市的此三個經濟指標統計數據絕對誤差的平均值分別小于Y省，即：H0:μBi＜μYi,H1:μBi≥μYi(i=1,2,3)，由 T 統 計 量 、Matlab計算得出此假設檢驗結果如下：

由Hi均等于0，pi值均接近于1可以看出，B市的地區統計數據質量優于Y省的相應地區統計數據質量。

同樣的，我們對B市和G省的地區統計數據的準確性進行比較。首先計算其相應指標相對誤差的絕對值，得到G省的數據質量準確性數據（見表1）。

利用擴展Scheffe[3]轉換法，將由B市和G省的地區統計數據的相對誤差絕對值構成的二總體B-F問題轉換為單總體問題：

由以上數據得到μ和Σ的估計：

用霍特林T2-檢驗方法對其進行均值向量檢驗：

對于給定的顯著性水平α=0.05下，p=P{ }F≥2.9961=0.0637因p=0.0637＞0.05=α，故接受原假設H0，即B市和G省的經濟統計數據質量沒有顯著性差異。如果取α=0.1，則接受B市和Y省的統計數據準確性質量有顯著性差異假設。

進一步，我們對它們的統計數據質量的優劣進行判斷和檢驗，對這兩地區的三個經濟指標的準確性大小分別進行判斷檢驗，比較其相對誤差絕對值的樣本均值大小。原假設為B市地區統計數據質量優于G省，即

對于給定的顯著性水平α=0.05下，利用Matlab軟件進行計算，如同上面分析B市和Y省地區統計數據質量的優劣性，經HotellingT2-分布計算得出此假設檢驗結果為：

由上述結果可以看出，B市的地區統計數據質量優于G省的相應地區統計數據質量。

繼而，我們對G省和Y省的地區經濟統計數據質量進行相應的分析，得出由它們的相對誤差絕對值構成的二總體B-F問題轉換為單總體問題的μ和Σ的估計：

用霍特林T2-檢驗方法對其進行均值向量檢驗：

經計算得檢驗統計量：

對于給定的顯著性水平α=0.05下：

因p=0.1342＞0.05=α，故接受原假設H0，即G省和Y省的經濟統計數據質量沒有顯著性差異，但是0.1342與0.05接近，如果取α=0.1雖然也接受G省與Y省統計數據準確性質量沒有顯著性差異，但0.132與0.1很接近，0.132處于臨界的區域，使得沒有顯著性差異的檢驗結果難以接受也不好拒絕。

這時如果對它們的統計數據質量準確性的優劣進行判斷和檢驗，對該兩地區的三個經濟指標的準確性大小分別進行判斷檢驗，比較其相對誤差絕對值的樣本均值大小。原假設為G省地區統計數據質量優于Y省，即

對于給定的顯著性水平α=0.05下，利用Matlab軟件進行計算，經計算得出此假設檢驗結果為：

由上述結果可以看出，G省的地區統計數據質量優于Y省的相應地區統計數據質量。通過以上分析檢驗可得，此三地區的地區統計數據質量的好壞依次為B市優于G省優于Y省。

4 結論

本文對B市、G省和Y省經濟統計數據中的地區生產總值(GDP)、全社會固定資產投資總額(FAI)、城鎮居民最終消費支出(FCE)統計數據的數據質量的研究，構建地區統計數據B-F問題，檢驗了三地區上述經濟指標的統計數據質量準確性是否具有顯著性差異，并對其準確性差異進行了對比和檢驗，得出統計數據質量準確性順序為B市準確性?G省準確性?Y省準確性。進一步的研究可以將該方法用于對同一個地區的統計數據質量準確性做歷史階段比較；也可將該方法用于各個地區的統計數據準確性排序比較，以便將各個省市區的數據質量評價為幾個數據質量準確性等級；另外可以考慮克服量化困難將該方法用在統計數據質量八個方面[8]的其他方面,因此該方法對于提高統計數據質量的準確性外的其他方面也有著一定的意義和作用。

[1]BV Behrens.Ein Beitrag zur Fehlerberechnung Bei Wenige Beobachtungen[J].Landwirtch.Jb,1929，(6).

[2]RA Fisher.The Fiducial Argument in Statistical Inference[J].The An nals of Eugenics,1935，(6).

[3]Scheffe H.On Solutions of the Behrens-Fisher Problem,Based on the T-distribution[J].Ann Math Statist,1943，(14).

[4]Welch B L.The Generalization of Student’s Problem when Several Different Population Variances are Involved[J].Biometrika,1947，(34).

[5]Bennett B M.Note on a Solution of the Generalized Behrens-Fisherproblem[J].Ann Inst Statist Math,1951，(2).

[6]Anderson T W.An Introduction to Multivariate Statistical Analysis[M].New York:Wiley,1984.

[7]Zhang JinTing,Xu JinFeng.On the K-sample Behrens-Fisher Problem for High-dimensional Data[J].Science in China Series A:Mathematics,2009，(6).

[8]孫明偉，龔敏慶.地區統計數據質量B-F問題研究[C].淄博第二屆信息、電子計算機工程國際學術會議論文集,2010,(11).

[9]中華人民共和國國家統計局.中國統計年鑒-2009[M].北京:中國統計出版社,2009.