多維密度核估計的漸進正態性及穩健漸進正態性研究

張 波，劉鶴飛，陳 興，郭洪亮

(1.云南大學 數學與統計學院昆明 650031；2.曲靖師范學院 數學與信息科學學院，云南 曲靖 655011）

0 引言

多維密度核估計的漸進正態性及穩健漸進正態性是非參數密度估計的一個非常重要的研究方向，其中非參數概率密度核估計作為非參數密度估計的重要方法，受到越來越多的學者的重視。Hardel、Miiller、Silverman、Scott等都曾致力于多維密度核估計的研究，Schuster、Singh、Susan,Walter、陳桂景、趙林成、楊振海等人得到了較好的相合速度的結果。其中Loftsgarden和Qnesenberry提出了最近鄰估計，Devroye和Wagner討論了一種窗寬依賴于樣本的核估計。Gasser、Mammitzsch和Granorsky對最優核理論做了廣泛的發展，Falrell、Hasminskii和Stone對核估計的最優收斂速度做了研究，Loader、Hjort和Jones研究了核函數的局部似然估計，相依數據的核密度估計的早期工作者是Roussas和Rosenblatt，他們建立了局部漸近正態性，Claeskens和Hall研究了核密度估計的MISE、ISE。雖然非參數概率密度核估計的理論主要集中在大樣本上，且在應用上需要大量的數據以及復雜的運算過程，但是隨著計算機技術的發展，非參數密度核估計的應用也變的越來越廣泛，其應用領域逐漸涉及社會學、物理學、生物學、以及各種工程技術領域。本文將討論多維密度核估計的漸進正態性，以及在大樣本情況下的穩健漸進正態性。

1 多維密度核估計的漸進正態性

1.1 多維密度核估計的漸進正態性的定義

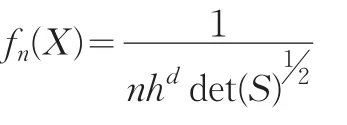
1.2 幾個相關引理

引理1[1]若K(u)和f(X)滿足條件

引理2[1]若K(u)和f(X)滿足條件

引理4若K(u)和f(X)滿足條件

則對于多維密度核估計，具有如下公式：

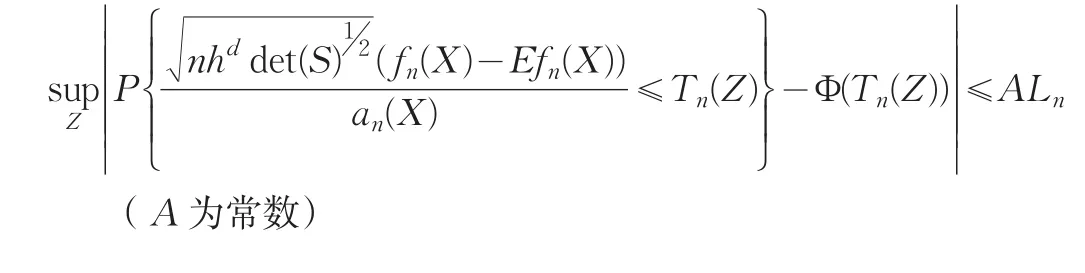
將Berry-Esseen不等式推廣到n維則對于多維密度核估計有下式：

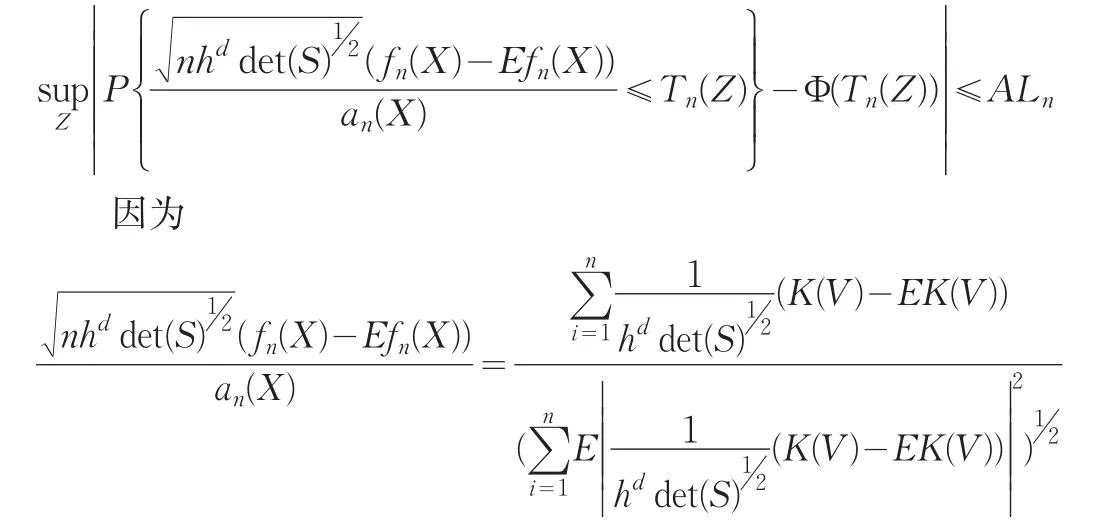
故引理得證。

1.3 多維密度核估計的漸進正態性定理及證明

定理1若K(u)和f(X)滿足條件

2 多維密度核估計的穩健漸進正態性

本文將概率密度一維穩健漸進正態性的定義[3]推廣到多維密度核估計中，在一定條件下我們給出多維密度核估計的穩健漸進正態性定理，并證明此定理。

定理2若K(u)和f(X)滿足條件

則上式多維密度核估計是穩健漸進正態的。

證明：首先將一維概率密度核估計的均方相合性定義[1]推廣到多維并應用到本文所提的多維概率密度核估計中，來證明多維密度核估計的均方相合性。即：

再利用穩健漸進正態性的定義及其在多維上的推廣，并應用到多維密度核估計的穩健性漸進正態性的證明中，即

3 結語

本文基于非參數密度估計尤其是非參數密度核估計的基本原理和統計方法將以往多維密度核估計文獻中的相關理論從一維推廣到多維，并證明了多維密度核估計的漸進正態性和穩健漸進正態性。

[1]陳希孺.非參數統計[M].上海：上海科學技術出版社，1989.

[2]熊祖光，非參數核密度估計的空間聚類算法研究以及改進[J].吉林大學學報，2008.

[3]鄭忠國.Bootstrap方法和穩健性[J].數學年刊，1986，7A(1).

[4]K.B.Athreya.Bootstrap of the Mean in the Infinite Variance Case[J].Ann Statist,1987,(15).

[5]匡繼昌.常用不等式[M].濟南：山東科學技術出版社，2003.

[6]B.Efron.More Efficient Bootstrap Computation[J].Ann Statist Ass,1989,(3).