電子政務服務外包多階段的三方博弈模型

何有世，趙帥軍，張懷勝

（江蘇大學 工商管理學院，江蘇 鎮(zhèn)江 212013）

0 引言

電子政務服務外包，是指以合同或協(xié)議的形式，將全部或部分電子政務系統(tǒng)的業(yè)務外包給承包商，并由雙方共同承擔電子政務項目開發(fā)的收益和風險[1-2]。委托代理雙方可以從項目承建和維護中得到相應的回報，形成多贏的局面[3]。一般認為，代理人受委托建設電子政務項目工作是一個多階段項目。因此，建立政府與運營企業(yè)的多階段激勵機制十分重要。

國內外學者從不同角度對于政府與運營企業(yè)的激勵機制進行了研究。Francesca等[4]認為，分段投資是創(chuàng)業(yè)企業(yè)的一種激勵手段。Ram1y Elitzur利用多階段博弈模型，研究了風險投資家和企業(yè)家在簽訂合同時的道德風險問題。根據(jù)雙方多階段博弈，從而得到最優(yōu)合同設計以及風險投資家的最佳退出點[5]。趙敏等對Ramy Elitzur模型進行了一定的簡化，去除一個決策變量后模型變得簡潔[6]。張矢的、魏東旭等提出對Ramy模型進行改進，從最優(yōu)報酬機制設計、分階段投資的角度構建動態(tài)多階段投資模型[7]。任志濤提出電子政務建設項目管理的多階段的激勵機制設計[8]。任志濤、張睿提出利用多階段博弈分析推導出風險投資家與企業(yè)家的最優(yōu)激勵報酬合同、影響合同設計的諸多因素，以及風險投資家的最佳退出點等[9]。以上研究的熱點主要集中于多階段委托方和代理方的道德風險和最優(yōu)激勵，忽視了信息不對稱條件下第三方監(jiān)管問題。文獻[9]提出政府采用第三方監(jiān)督機制，沒有對模型深入研究。文獻[10]提出單階段三方動態(tài)博弈模型，對多階段第三方的研究還沒涉及。因此本文針對上述研究的不足，對多階段三方博弈進行研究，通過對Ramy模型的改進，構建多階段三方動態(tài)博弈模型，分析政府、監(jiān)督部門和承包商之間的最優(yōu)激勵和風險控制。

1 問題描述及基本假設

1.1 問題描述

電子政務開發(fā)一般存在兩種模式，一種是自主模式。自主模式容易混淆政府在電子政務發(fā)展過程中的角色和職能定位，分散政府部門對核心業(yè)務的專注程度；另一種是外包模式。外包模式將涉及項目建設中政府不擅長或不太擅長的業(yè)務外包給專業(yè)機構進行建設、運營以及管理和維護。外包常常使用競爭性招標投標方式選擇承包商，政府有權利選擇外包服務商，卻沒有動力去監(jiān)督外包服務商。因此，政府尋求信息監(jiān)理部門輔助政府監(jiān)督管理，承包商也需要政府和監(jiān)理部門參與管理。博弈參與人之間信息不對稱，各方群體的利益驅動和目標動機不同，這構成了政府、監(jiān)督部門和承包商三方博弈。

1.2 基本假設

假設博弈三方均為風險中性，第三方對其它兩方參與者可能采取的行動策略及其概率不了解或各參與者采用的行動策略具有不確定性。

博弈共分K階段進行，博弈三方都能觀察到外包共分K階段進行，不得在K階段前無故結束合同。

Vk為政府從k～K階段總期望收益，Jk為監(jiān)理方從k～K階段總期望收益，Uk為承包商從k～K階段總期望收益。

bk為外包成功時政府增值收益，sk為第k階段外包成功時政府給予承包商的獎勵，qk為外包成功時政府給予監(jiān)理部門的獎勵。外包不成功時不獎勵也不懲罰，qk值為0。pk為承包商未能按時按量完成時，政府為進行下階段外包的實施給予承包商的保障費用。

第k階段外包成功的概率和監(jiān)督成功的概率分別為ak（ek）、hk（fk），外包成功的概率滿足：0≤ak(ek)≤1,?ak(ek) ?ek＞0,?2ak(ek) ?ek2＜0 監(jiān)督成功的概率滿足：0≤hk(fk)≤1,?hk(fk) ?fk＞0,?2hk(fk) ?fk2＜0

△βk為監(jiān)督方發(fā)現(xiàn)承包商工作不努力時給予的懲罰，懲罰費用歸監(jiān)督方。同時承包商將損失成本△βk，監(jiān)督方未能發(fā)現(xiàn)承包商不努力或外包不成功時△βk都為0。

c(fk)、c(ek)分別為監(jiān)理部門、承包商階段性成本費用。C'(ek)＞0，C''(ek)＞0。監(jiān)督部門的監(jiān)督力度增大有 C'(fk)＞0，即C''(fk)＞0。

2 多階段三方博弈模型

第k階段及下一階段政府收益模型：

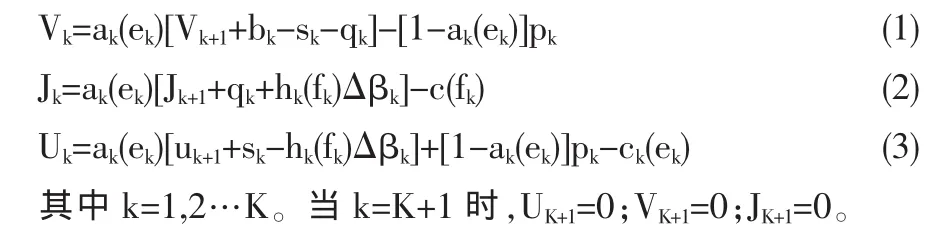
該模型表示，第k階段成功時，政府分別給予監(jiān)督方和承包商獎勵qk、sk。若監(jiān)督方發(fā)現(xiàn)代理方投機取巧，則對其懲罰△βk。未監(jiān)督到承包商有過失行為或外包延期，不做懲罰，即△βk值為0。承包商在外包成功時，接受政府激勵。外包延期時，利用政府給予的費用pk，保障項目階段性完工。不管外包成功與否，監(jiān)督方和承包商付出成本費用。若qk和△βk同時為0，即監(jiān)督方不存在，出現(xiàn)政府和承包商的雙方博弈。在多階段博弈中，三方的利潤都與承包商的努力程度有關。監(jiān)督方和承包商利潤與監(jiān)督的力度有關。政府、監(jiān)督方和承包商博弈三方的目標函數(shù)分別為：

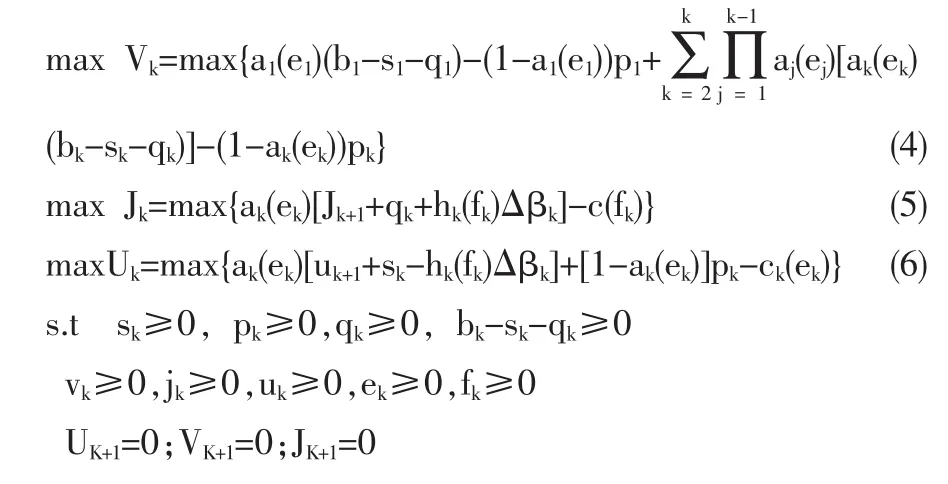
3 模型分析

模型博弈的主體是政府、監(jiān)督部門和承包商。他們各自目的是通過選擇自己的行動，以最大化自己的收益。對成功因素 ek和監(jiān)督因素 fk及四個決策變量 sk、pk、qk與 △βk。 分別考察如下：

公式（2）對 fk求導：

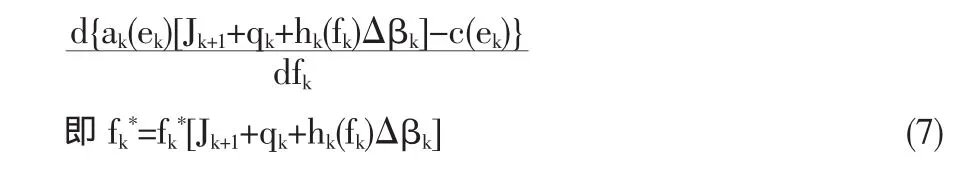
公式（3）對 ek求導：

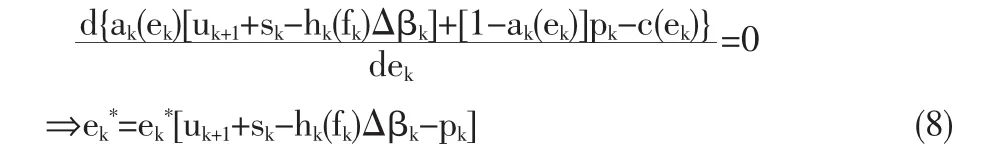
若承包商的努力程度ek和監(jiān)督部門的監(jiān)督力度fk為常數(shù)時，k=1,2，…K，m≤k。考察承包商對各參數(shù)的變化情況，公式（1）對 sk求導并把公式（8）代入：

結論1：從式（11）可見，在分階段博弈中，承包商的成功率與保障的邊際正相關。政府要保障外包項目高效率完成，應對承包商提供更加完善的保障。反之從公式（12）可見，對承包商來說，監(jiān)督懲罰的邊際遞增。因此，監(jiān)督方應降低懲罰要求，以防止承包商因為懲罰過多而自身收益得不到保障。此時政府應采取增加保障費用或降低對監(jiān)督方的激勵成本策略。

根據(jù)式（10）、（11）、（12）可以得到政府和監(jiān)督方對承包商在第一階段就確定了最佳激勵策略sk*、最佳保障pk*和最佳監(jiān)督策略△βk。所以對政府和監(jiān)督方在第一階段的期望收益求一階導，先對sk求導并把公式（8）代入有：

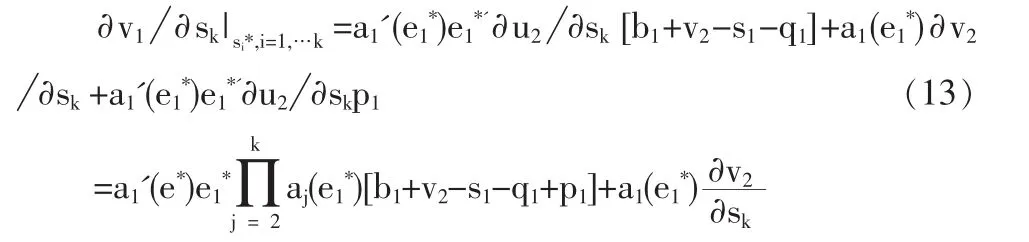
式（13）等于 0，推出：

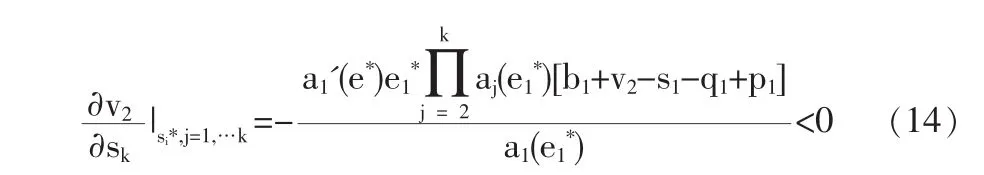
根據(jù)式（14）得到：

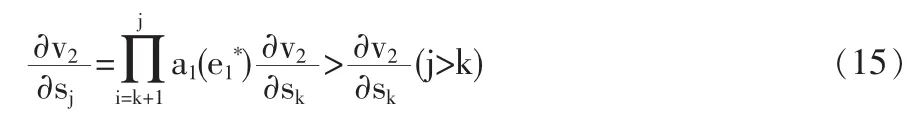
根據(jù)（13）式，如果有任意一個m、k。存在：

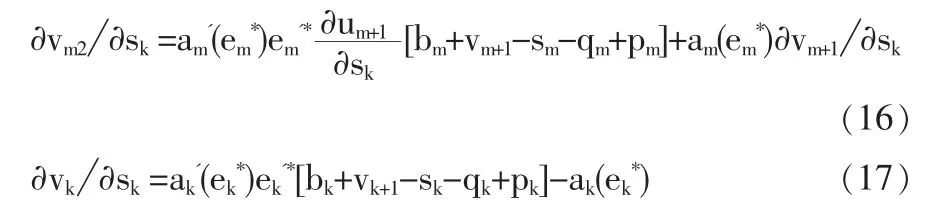
對式（16）迭代，將式（17）代入式（13）有：

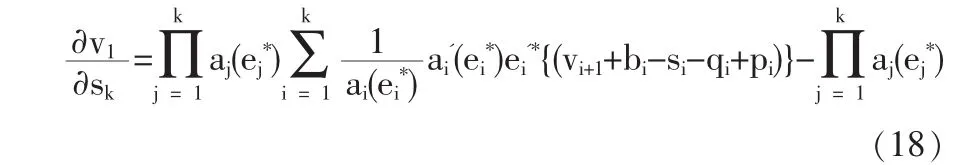
根據(jù)公式（18）得到：

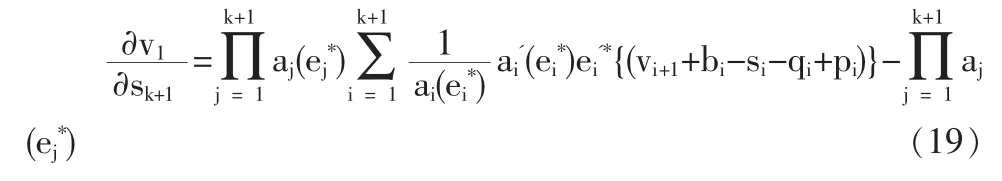
將公式（19）提取第k+1項有：

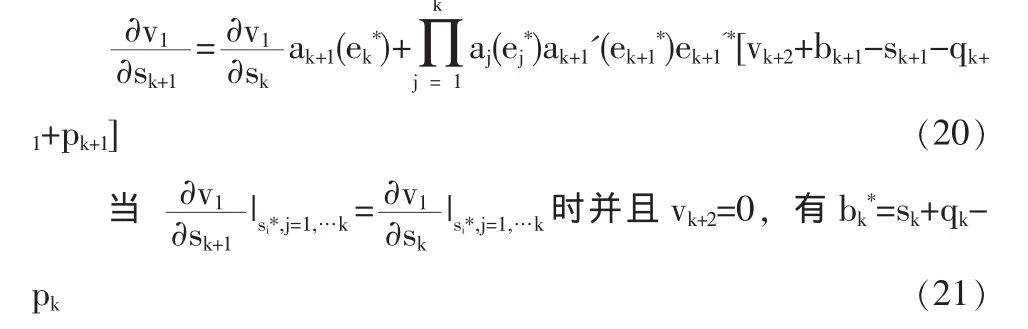
根據(jù)式（21），?1≤ξ≤K，使得：

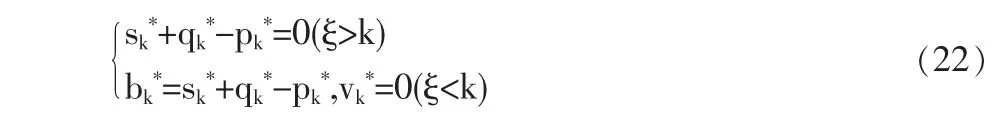
當 bk*＞sk+qk-pk時，?v1?sk+1＞?v1?sk邊際遞增。 bk*＜sk+qkpk時?v1?sk+1＜?v1?sk邊際遞減。 同理可證，類似?v1?sk可推得?v1?pk、?v1?qk得到同樣的結論。

結論2：從式（22）可得，對第k階段，當政府的收益大于對承包商的激勵、監(jiān)督方的激勵和保障費用之和時，政府的邊際收益遞增。即政府的收益越大，給予承包商的獎勵越多。同理推得，政府收益越多，政府給予監(jiān)理部門的獎勵和給予承包商的保障費用的邊際也遞增。說明博弈三方收益正相關。要實現(xiàn)共贏，前提條件是承包商利益得到保障。

根據(jù)：

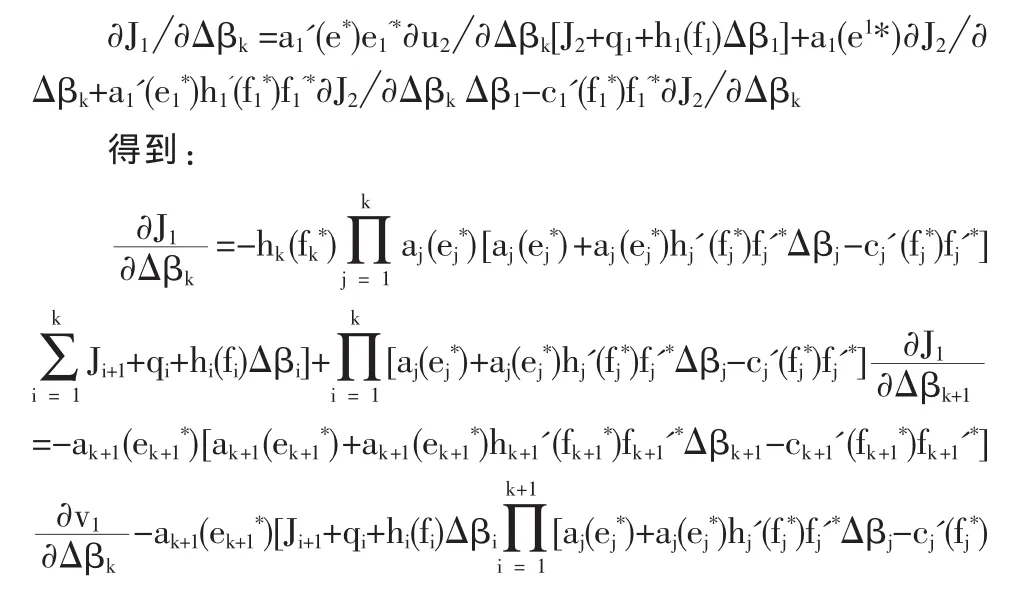
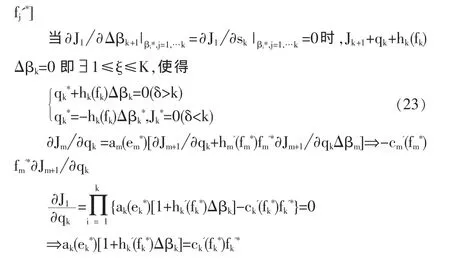
上式對qk求積分并合并積分常數(shù)得到：

比較（23）與（24），顯然（24）退出的條件要早于（23）的條件，即成功條件下監(jiān)督方接受政府的期望獎勵與監(jiān)督的期望費用之和等于自身費用時，選擇退出。

結論 3：從式（23）可得，政府的最佳退出點 ξ滿足 sξ+qξ=pξ，即第ξ階段承包商和監(jiān)督方的激勵費用之和與保障費用處于均衡。可得監(jiān)督方最佳退出點滿足式（24），即監(jiān)督方收益和支出平衡。

根據(jù)結論 3：當k＞ξ時，政府總收益vk為 0，有 bk=sk+qkpk。?1≤ξ≤K，政府增值收益bk為0時，即政府收益已經不再增加，即第k階段承包商和監(jiān)督方的激勵費用之和與保障費用處于均衡時。此時政府考慮退出，認為ξ是政府最佳退出點。如果?階段外包尚未完成，政府通過增加激勵費用或監(jiān)督費用的策略保障項目運營。監(jiān)督方最佳退出點為式（24），即監(jiān)督方收益和支出平衡時。監(jiān)督方再無收益，監(jiān)督方首選退出博弈。若監(jiān)督方先達到退出點ζ，政府為保障項目繼續(xù)運營可以增加對監(jiān)督方的激勵。承包商為獲得更多的利益，應主動要求與政府進行多階段合作。由此可知政府享有三方博弈的主導地位。

以政府為主導的三方委托代理關系，當政府達到最佳退出點選擇退出時，三方博弈結束。在最佳退出點ξ處，若成功的概率ak(ek,fk)為固定常數(shù)a時，博弈三方變成k階段的重復博弈。此時，政府的最大收益為v1，監(jiān)督方的收益為j1，監(jiān)督方的收益隨著k的增加而增加，即合作的次數(shù)越多，監(jiān)督方的利潤越豐厚。承包商的收益為u1。

將式（1）（2）（3）展開并將 a 代入有：

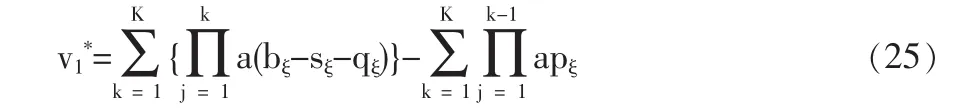
若在最佳退出點處，政府尚未對承包商采取激勵政策和保障政策，此時 sξ-1-1=0，sξ＞0， pξ-1=0，pξ＞0，根據(jù)式（25）?qξ-1=0。此時政府的收益范圍：

監(jiān)督方K階段的收益與k+1階段比較有：

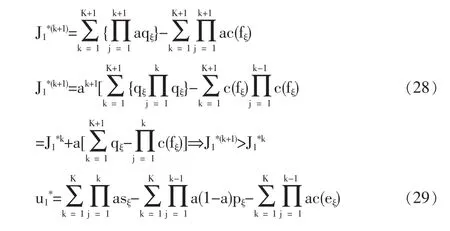
4 數(shù)值分析

某電子政務外包分成3個階段，即K=3。設成功的概率ak(ek*)=mi(0.8ek,1)，監(jiān)督成功的概率 hk(fk*)=min(0.2fk*,1)，每階段都成功，所以pk=0。承包商自身費用假設為c(ek)=e2k，監(jiān)督方自身費用假設為 hk（fk）=2fk。另外定義 ek*=0.4[sk-hk(fk)△βk+uk+1],fk*=0.1[qk+hk(fk)△βk+Jk+1]當 b3=s3+q3時，給定 bk、sk、qk數(shù)值如表1，代入 f3=0.1[q3+h3(f3)]，求出 f3=0.1；e3=0.4[s3-h3(f3)△β3]得到e3=0.4；f2=0.1[q2+h2(f2)+J3]和 J3=a3（e3）[q3+h3（f3）△β3]-c(f3)得到f2=0.06。其它同理。數(shù)據(jù)如外包成功案例表（見表1）。

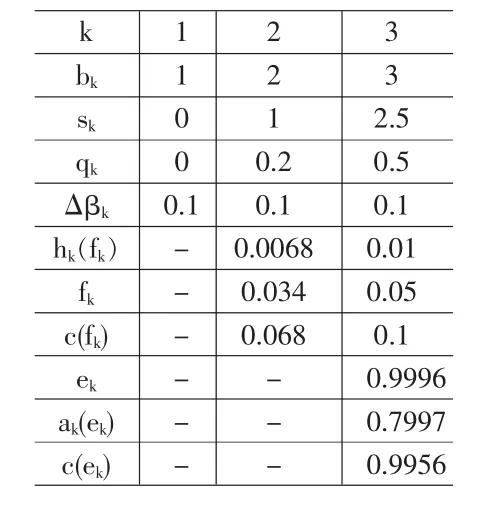
表2 外包失敗案例表

經計算求出 a1(e1)=0.03，a1(e1)b1+a2(e2)b2=0.384，v1=0.031。滿足式（26）的要求。說明在最佳退出點處，政府收益最大值為0.031。

同外包成功案例表的解法，當計算到f2這一項時，J3因為費用過大成為負數(shù)，導致過程終止。即不符合式（24）。比較兩表中數(shù)據(jù)s3和q3，政府對承包商激勵較高，對監(jiān)督方激勵偏低，對承包商激勵過高導致承包商費用過大，是此過程失敗的主要原因。若保障此項目順利實施，最好的做法是政府提高對監(jiān)督方的激勵費用。通過算例說明為防止承包商投機行為發(fā)生，政府采用的策略是激勵監(jiān)督方，而不是激勵承包商。由此可以說明委托代理過程中監(jiān)督方的重要性。

5 結語

本文在動態(tài)框架下研究政府、監(jiān)督方和承包商之間三方博弈問題。正確處理好三者關系問題是解決電子政務建設的關鍵。通過改進Ramy Elitzur模型，提出政府、監(jiān)督方和承包商在多階段博弈中各自采取的最佳策略。根據(jù)模型分析得出政府為保障項目順利實施，可以增加對承包商的獎勵費用。或者采用間接策略增加監(jiān)督費用，通過監(jiān)督方的努力來督促承包商努力工作。根據(jù)模型分析發(fā)現(xiàn)，監(jiān)督作用在委托代理問題中不可缺少。而保證政府和監(jiān)督方收益的前提是承包商的收益得到保障。因此本文對多階段博弈三方的研究是有必要的，對外包過程中風險防范有一定的理論指導意義。

本文博弈模型是建立政府、監(jiān)督和承包商三方基礎之上，而現(xiàn)實中監(jiān)督方通常是輔助政府工作，兩者利益一致。本文沒有考慮政府和監(jiān)督方之間利益一致問題，而這種情況可能會損害承包商的利益。因此在電子政務外包過程中三方問題研究仍需不斷的改進。另外，現(xiàn)實中有政府、承包商和公眾三方博弈也是值得研究的課題。

[1]Yang C,Huang J B.A Decision Model for iS Outs Ourcing[J].International Journal of Information Management,2000,(20).

[2]Smith M A,Kumaur R L.A Theory of Application Service Provider(AsP)use from a Client Perspective[J].Information&Management,2004，(41).

[3]陸敬筠,仲偉俊,王加中,梅姝娥.電子政務服務外包模式BOO和BOT的比較研究[J].管理學報，2010,7(5).

[4]Cornelli F,Ybsha O.Stage Financing and the Role of Convenible Debt[C].Working Paper Series,1998.

[5]Elitzur R,Gavious A.A Multi-period Game Theoretic Model of Venture Capitalists and Entrepreneurs[J].European Journal of Research,2003,2(144).

[6]趙敏,李湛,王榮.基于道德風險的科技創(chuàng)業(yè)企業(yè)多階段投資博弈決策模型[J].上海交通大學學報，2006,40(4).

[7]張矢的,魏東旭.風險投資中雙重道德風險的多階段博弈分析[J].南開經濟研究,2008,(6).

[8]任志濤.建筑業(yè)信息化的博弈分析[D].天津大學博士論文，2004,2(3).

[9]任志濤,張睿.電子政務服務外包及其激勵機制分析[J].中國軟科學,2007,(7).

[10]李致平,董梅生.腐敗的三方動態(tài)博弈模型及其治理對策[J].運籌與管理,2003,12（3）.