通過幾何誤差分區(qū)來提高數(shù)控機床加工精度的研究*

王曉峰 范晉偉 王稱心 宋貝貝

(北京工業(yè)大學(xué)機電學(xué)院，北京100124)

機床的幾何誤差占到整個機床誤差的20%～30%［1］，因此對幾何誤差的辨識及補償是提高機床加工精度比較有效的方法。本文提出了一種新的誤差分區(qū)補償方法，通過與傳統(tǒng)點補償方法的對比計算，確實對機床的加工效率和加工精度都有一定的提高。

1 機床幾何誤差的描述及誤差源

1.1 幾何誤差的描述

機床的幾何精度與零件工作面的幾何精度、運動件的運動精度、零部件之間及其運動軌跡之間的相對位置精度等密切相關(guān)，它是保證加工精度的最基本條件。機床制造誤差對工件加工精度影響較大的有:主軸回轉(zhuǎn)誤差、導(dǎo)軌誤差和傳動鏈誤差。主軸回轉(zhuǎn)誤差是指主軸各瞬間的實際回轉(zhuǎn)軸線相對其平均回轉(zhuǎn)軸線的變動量。導(dǎo)軌誤差主要包括在垂直面內(nèi)的直線度，在水平面內(nèi)的直線度，前后導(dǎo)軌的平行度(扭曲)，除了導(dǎo)軌本身的制造誤差外，導(dǎo)軌的不均勻磨損和安裝質(zhì)量，也是造成導(dǎo)軌誤差的重要因素。傳動鏈誤差是指傳動始末兩端傳動元件間的相對運動的誤差。

1.2 多軸機床的幾何誤差源［2］

一個物體在空間由6個自由度來確定它的位置(定位和方向)，這些自由度構(gòu)成了3個平移和3個轉(zhuǎn)角，所以1個物體的實際定位和方向與所期望值相比具有6個誤差源。機床的滑座是1個在空間被限制了5個自由度的物體，由于導(dǎo)軌的幾何缺陷，滑座在運動中表現(xiàn)出直線度誤差、繞3個軸的轉(zhuǎn)角誤差和沿導(dǎo)軌定位誤差。

圖1描述了滑座—導(dǎo)軌系統(tǒng)的運動誤差。δ表示平移運動誤差，ε表示轉(zhuǎn)角運動誤差;下標表示平移誤差的作用方向或轉(zhuǎn)角誤差轉(zhuǎn)動軸的方向;括號內(nèi)的字母表示平移運動的方向。所有誤差都是移動距離的函數(shù)。

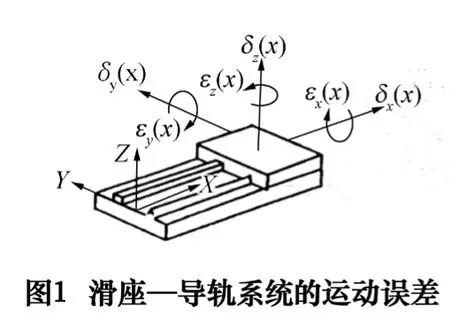
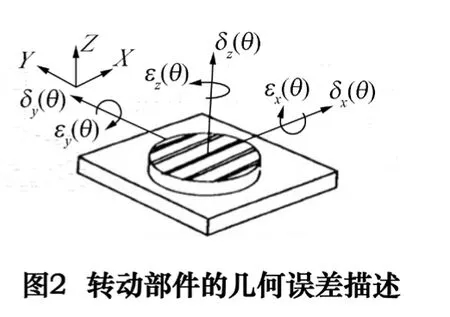
圖2描述了轉(zhuǎn)動部件的幾何誤差。與直線運動的幾何誤差定義相似，δ表示平移誤差，ε表示轉(zhuǎn)角誤差;下標表示平移誤差的作用方向或轉(zhuǎn)角誤差轉(zhuǎn)動軸的方向;括號內(nèi)的變量表示轉(zhuǎn)動的角度。所有誤差都是轉(zhuǎn)動角度的函數(shù)。

機床各坐標軸之間還存在垂直度誤差。這些誤差構(gòu)成了幾何誤差源。

2 幾何誤差的分區(qū)

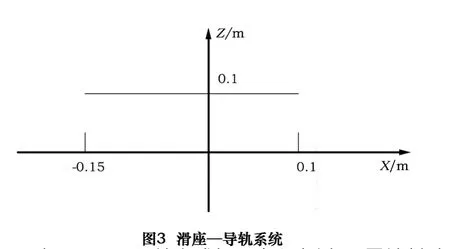
由于機床在運動過程中各個部件的磨損程度不一樣，最終將導(dǎo)致在不同的運動區(qū)域，機床的幾何誤差不盡相同。拿滑座—導(dǎo)軌系統(tǒng)來說(如圖3所示)，在1個1 m長的導(dǎo)軌上，可能在0～50 mm的范圍內(nèi)平移誤差、轉(zhuǎn)角誤差都變化不大，但在50～100 mm范圍內(nèi)的平移誤差、轉(zhuǎn)角誤差和0～50 mm的平移誤差、轉(zhuǎn)角誤差卻相差很大，這就需要我們將1根導(dǎo)軌按誤差變化情況，對幾何誤差進行分區(qū)處理，并且將幾何誤差變化不大的劃分到一個區(qū)域。

以MAKINO三軸立式加工中心為例，現(xiàn)需銑削以下工件:

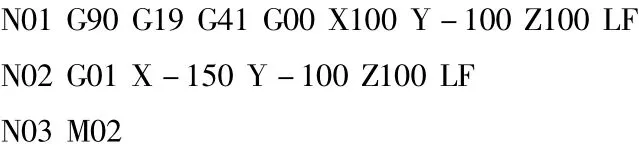
利用多體理論對MAKINO進行誤差建模可以得到，考慮幾何誤差的MAKINO立式加工中心的實際刀具路線方程為:

式中:δx(x)、δy(x)、δz(x)為沿X 軸移動時產(chǎn)生的 x、y、z方向的線位移誤差，εx(x)、εy(x)、εz(x)為沿 Y 軸方向移動時產(chǎn)生的x、y、z方向的角位移誤差。同理可得沿Y軸、Z軸的線位移誤差和角位移誤差的字母表示;εxy、εyz、εzx分別為 X、Y 軸的垂直度誤差，Y、Z 軸的垂直度誤差和Z、X軸的垂直度誤差;q4x、q4z為主軸箱上端面中心在機床設(shè)定坐標系中的投影，xp、yp、zp為工件坐標系內(nèi)的刀具路線上的給定點，qwx、qwy、qwz為工件坐標系上的理論刀具中心點相對于系統(tǒng)坐標系的位置陣列，設(shè)定 q4x=0.1 m，q4z=0.1 m，qwx=0，qwy=0，qwz=0.1 m(如未特殊說明，下文單位均為m)。

假設(shè)從X軸上的0至0.1 m處為區(qū)域一，從X軸上的－0.15 m到0處為區(qū)域二，在各區(qū)域內(nèi)的幾何誤差值相同，如表1所示。

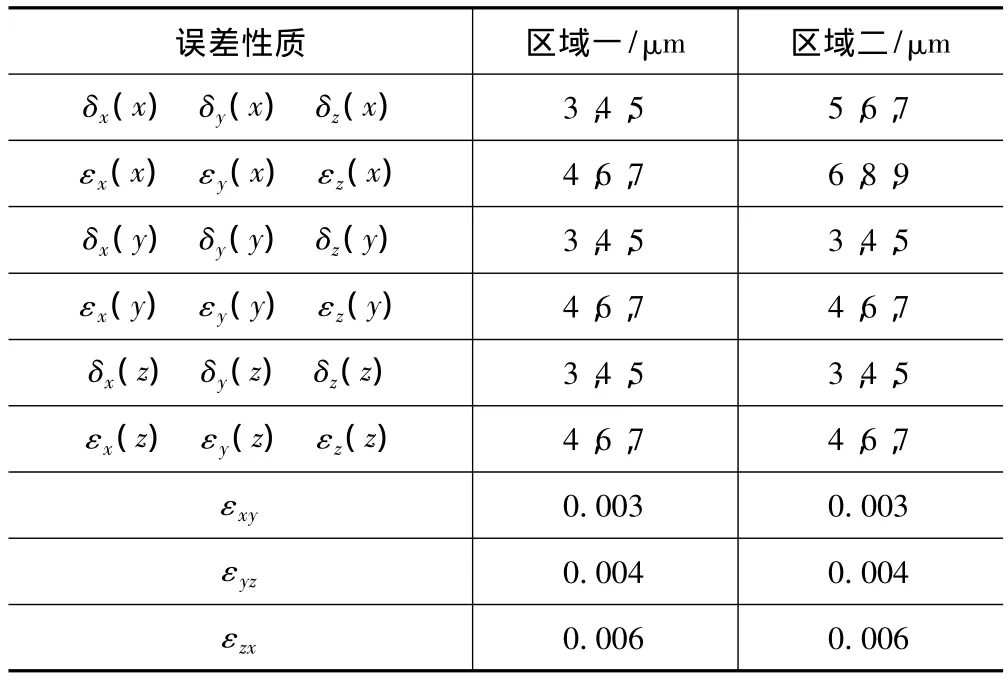
表1

對區(qū)域一，將表中各個變量代入式(1)、(2)、(3)可得:

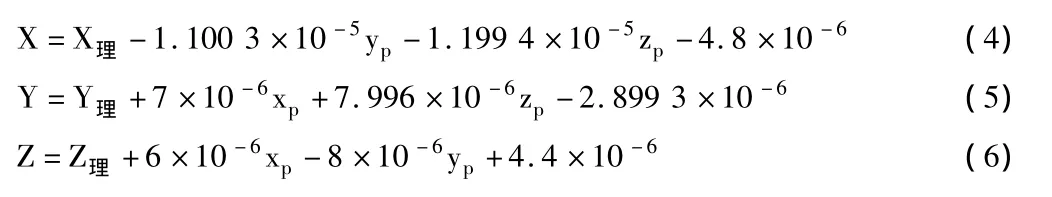
將本區(qū)域內(nèi)的(X理、Y理、Z理)的起點位置(0.1，－0.1，0.1)及終點位置(0，－0.1，0.1)代入式(4)、(5)、(6)可得實際的(X，Y，Z)坐標應(yīng)為

起點:(0.099 996 2，－0.100 002 1，0.100 006 0)終點:(0.000 003 8，－0.100 002 1，0.100 006 0)

由上述計算可知理想坐標與實際坐標的差距為

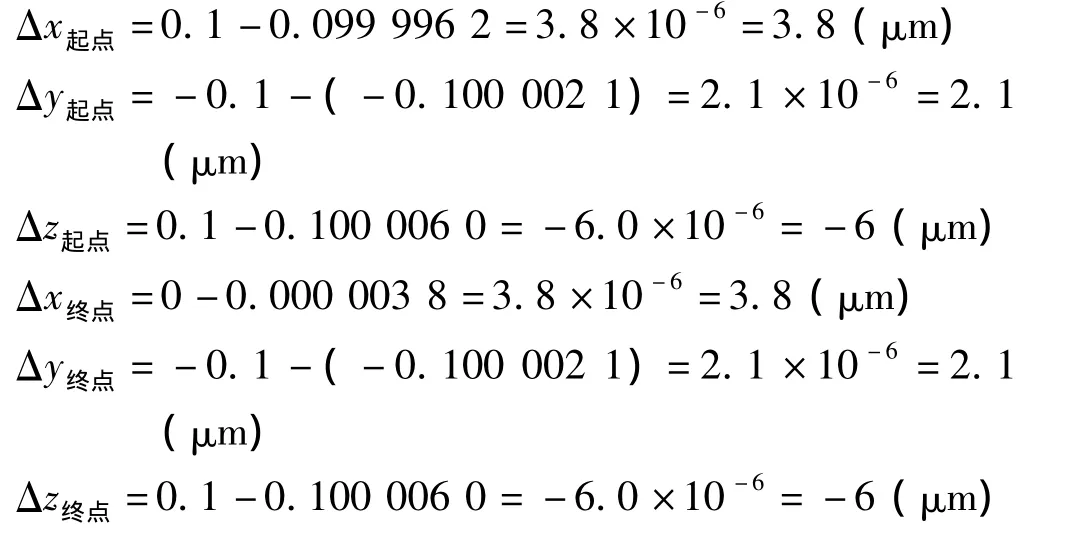
對區(qū)域二，將表中各個變量代入式(1)、(2)、(3)可得:

將本區(qū)域內(nèi)的(X理、Y理、Z理)的起點位置(0，－0.1，0.1)及終點位置(－0.15，－0.1，0.1)代入(4)、(5)、(6)式可得實際的(X，Y，Z)坐標應(yīng)為

起點:(－0.000 003 8，－0.100 006 2，0.100 002 2)

終點:(－0.150 003 8，－0.100 006 2，0.100 002 2)

由上述計算可知理想坐標與實際坐標的差距為

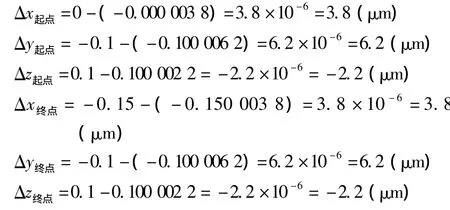
按以往的方式生成的G代碼為:

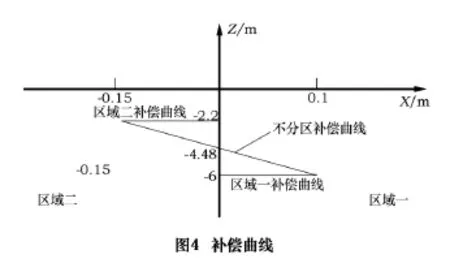
如圖4所示，圖中斜線即為未分區(qū)時Z方向的誤差隨X軸位移的變化曲線，區(qū)域一和區(qū)域二的水平線為分區(qū)時Z方向的誤差隨X軸位移變化曲線。由圖可知，在區(qū)域一需要的補償量在理想狀態(tài)下應(yīng)該為6 μm，而采用未分區(qū)的方式補償量是變化的，在X=0處與理想的偏差最大為Δzmax=|－6－(－4.48)|=1.52(μm)，在區(qū)域二需要的補償量在理想狀態(tài)下應(yīng)該為2.2 μm，而采用未分區(qū)的方式補償量同樣是變化的，在X=0處與理想的偏差最大為Δzmax=|－4.48－(－2.2)|=2.28(μm)。

通過分析，我們對上述G代碼進行區(qū)域一和區(qū)域二劃分的方式來進行修改，精確的G代碼如下:

3 結(jié)語

通過對機床的誤差源進行分析，提出了以誤差分區(qū)的方式來建立誤差模型，通過對機床的加工指令的修改，提高了數(shù)控機床的加工精度。

［1］李圣怡，戴一帆，等.精密和超精密機床精度建模技術(shù)［M］.北京:國防科技大學(xué)出版社，2007:23.

［2］范晉偉.基于多體運動學(xué)的數(shù)控機床運動建模及軟件補償技術(shù)的研究［D］.天津:天津大學(xué)，1998.