股指收益率與成交額間引導關系分析

吳明華，周愛民，宋敏

（南開大學經濟學院，天津300071）

股指收益率與成交額間引導關系分析

吳明華，周愛民，宋敏

（南開大學經濟學院，天津300071）

文章運用風險研究領域中應用廣泛的Copula分析法，考察我國上證指數及深成指日收益率與成交額之間的相互引導關系。結論顯示，成交額變動率與滯后其一個交易日的股指收益率之間不存在引導關系；股指收益率對滯后其一個交易日的成交額變動率存在先導作用，不過這種先導作用對滯后其兩個交易日的成交額變動率不存在。此外，股指收益率與滯后其一個交易日的成交額變動率間的關聯模式表現為尾相關。

收益率；成交額；Copula模型

0 引言

交易量與股價（股指）作為市場行為信息指標，由于直接反應股票（股市）的交投情況而備受市場關注，量價之間的關系也一直是技術分析領域中的研究熱點。華爾街有兩句諺語：“牛市成交量大，熊市成交量小”及“量推價走”，更通俗的說法即是：“價漲量增、價跌量減”，“量在價先行”。

成交量與價格之間到底是否存在著相互引導關系？許多學者曾對這個問題進行過研究。Hiemstra and Jones（1994）[1]研究了道瓊斯綜合指數日收益率與成交量間的引導關系，結論顯示二者存在著顯著的雙向非線性因果關系。Silvapulle and Choi（1999）[2]采用Granger因果檢驗法對韓國股票市場指數日收益率與成交量間關系進行研究，結果顯示二者具有雙向線性和非線性因果關系。我國學者對交易量與收益變動的引導關系也進行了大量的研究，不過結論差異較大。魏巍賢,康朝鋒（2001）[3]利用上證綜合指數日收益率與成交量數據，研究發現價格和成交量對預測對方有顯著作用。芮萌、孫彥叢與王清和（2003）[4]對滬深A、B股日交易數據進行研究，結論顯示任何一個市場上交易量均不Granger引導市場收益。張博（2008）[5]以上海A股綜合指數日收益率及日交易金額數據為分析對象，研究結論認為交易量中的信息交易量對于價格變動具有較高的解釋能力，且該市場存在價量之間雙向Granger因果關系。董秀良,吳仁水（2008）[6]利用中國滬深股市日交易數據，采用多元GARCH模型進行實證研究，結論顯示滬市股指收益與成交量間具有雙向引導關系，而在深市只存在收益對成交量變化的單向引導關系，不過文章作者指出，滬市指數編制存在問題，因此判定收益對成交量變化具有單向先導作用。

從股指走勢圖中觀察，量價間引導關系具有不確定性。通常，價格及交易量小幅波動時，二者間關聯關系很難捕捉，而波動較大的量、價在實踐中受到重點關注。本文借鑒在風險研究領域中應用廣泛的Copula分析法，并首次將其引入量價關系的研究中。采用Copula分析法一方面可以找到量與價的聯合分布，另一方面可以發現量價變化較明顯時二者間的關聯關系。

1 Copula分析法

1.1 本文所涉及的二元Copula函數簡介[10]

1.1.1 Gumbel Copula函數

Gumbel Copula函數的分布函數和密度函數分別為：

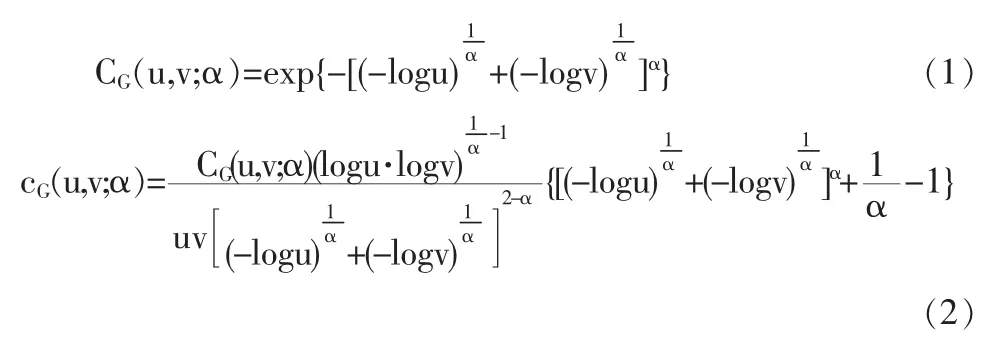
其中α（α∈（0，1]）為相關參數。當α=1時，CG（u,v;α）=u· v，隨機變量u、v相互獨立；當α→0時，隨機變量u、v趨向于完全正相關。

1.1.2 Clayton Copula函數Clayton Copula函數的分布函數和密度函數分別為：

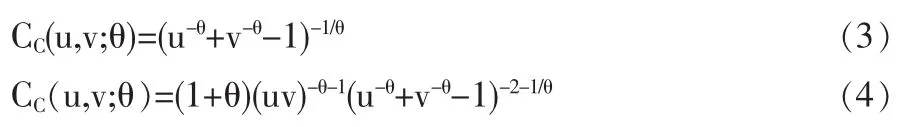
1.1.3 Frank Copula函數Frank Copula函數的分布函數和密度函數分別為：

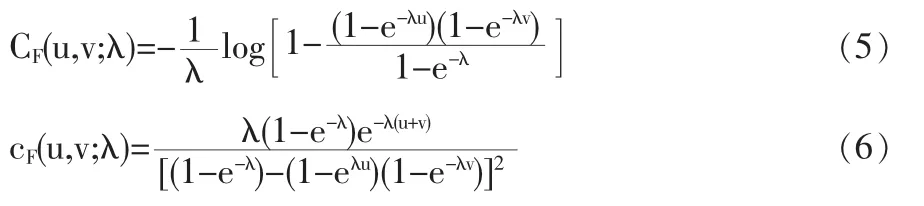
此外，用線性組合的方法，可以根據已有Copula函數構造更多的Copula函數（參考Nelsen（1998）[8]），如由以上三個二元Copula函數可以構造混合Copula函數：

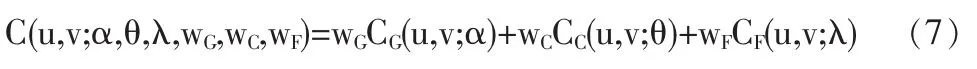
其中wG、wC、wF為權重，滿足wG+wC+wF=1，且0≤wG，wC，wF≤1。

1.2 Copula函數的參數估計

Copula函數的參數估計方法有很多（參見羅俊鵬（2005）[9]），其中偽極大似然估計法較為常用，該方法不需指定邊緣分布，從而可避免由錯選邊緣分布所導致的參數估計錯誤。偽極大似然估計法分為兩個步驟，下面以二元混合Copula函數的參數估計為例進行介紹。

首先，用經驗分布對邊緣分布建模如下：

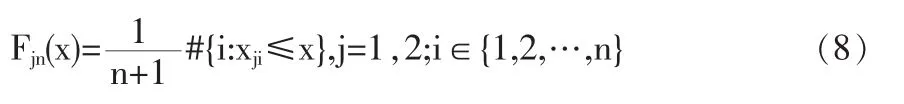
其中n為觀測值組數。這樣，每組觀測值Xi=(x1i，x2i)，i= 1，2，…，n，經式（11）變換后，得到相應擬觀測值：(ui,vi)=(F1n(x1i)，F2n(x2i))，i=1,2,…,n。

然后，基于已得擬觀測值，構造偽似然函數：

其中c(·)表示式（10）中混合Copula函數的密度函數，β=（α，θ，λ，wG，wC，wF）為待估參數。使式（12）中似然函數值極大化的估計值β贊，即為上述二元混合Copula函數的偽極大似然估計量。

1.3 擬合優度檢驗

根據已得偽極大似然估計量，可以確定二元Copula函數的具體形式，從而找出變量間的相關關系。然而所確定的Copula函數是否合適，還需進行擬合優度檢驗。由于我們采用偽極大似然法估計參數，相應可以選取邊緣分布未知時的χ2擬合優度檢驗。

設Apq，p=1，2，…，r；q=1，2，…，s是對區域[0，1]×[0，1]的一個劃分，相應地，令：

在所估計Copula函數合適的零假設之下，下列統計量M服從自由度為（r-1）(s-1)-m的χ2分布：

其中m為所估計Copula模型中包含參數的個數。

2 實證研究

2.1 數據來源與選取

本文選取我國上證指數，深圳成份指數的收盤值及成交金額序列為研究對象。之所以選取交易金額為反應交易量的指標，是因為各股票價格不一，且通常投資者以投入資金的多少來表征其對某只股票及市場前景的看好程度，因此認為交易金額比以股數為單位的交易量更能反應市場的交投狀況。各時間序列范圍為1999年8月2日至2010年2月9日，序列長度為2545。1999年7月，我國第一部《證券法》實施，盡管之后曾多次對其做出修訂，但該法案的實施，在一定程度上規范了市場交易行為。隨著監管的發展及市場的擴容，市場指數越來越不易被操縱，其價格與成交額能較真實地反應市場狀況及交易者行為。

數據來源于大智慧行情分析系統。所應用的數據分析軟件是MATLAB 7.1。

2.2 實證分析

由于股指收盤值與成交金額序列均為具有自相關性、異方差性的單位根過程，因此在進行Copula分析之前，需要將各序列處理為獨立同分布觀測值。首先為各序列取對數后做一階差分，分別以Rsh、Rsz與Ash、Asz表示對數上證指數、深圳成指收盤點數及成交金額序列差分后的值，即為滬、深股指收益率與成交額變動率序列。然后對各序列進行GARCH變換以去掉其自相關性及異方差性，結果見表1。

表1 各序列去自相關性及異方差性變換

變換后的各標準化殘差序列有效長度不同，為此我們取其第11-2545的子序列進行研究，各序列名稱不變，長度均為2535。此外，下文中的收益率及成交額變動率均指經GARCH變換后相應標準化殘差序列。

根據式（11），可得（ush，vsh）及（usz，vsz）的擬觀察值序列分別為：（Ush，Vsh）與（Usz，Vsz）。

2.2.1 收益率對成交額變動率的引導關系檢驗

為檢驗滬、深股市收益率對成交額變動率的引導關系，我們分別取Ush、Usz的前2534個值作為新序列Ushb、Uszb；取Vsh、Vsz的后2534個值作為新序列Vsha、Vsza，并組成兩對：（Vshb，Vsha）及（Uszb，Usza），采用Copula分析法分別進行研究。

應用偽極大似然法估計Copula參數，經計算，混合Copula模型的極大似然值最大，并計算相應擬合優度檢驗統計值M，結果見表2。

表2 Copula模型擬合結果

對上證指數考察時，由于第一組估計結果顯示混合Copula中Gumbel分布的權重值不顯著，將其去掉后重新進行估計，因而呈現了兩組估計結果。表2中的M值由式（15）求得，這里我們將區域[0，1]×[0，1]劃分為15×15個單元格。臨界值依次是自由度為190、192、190的χ2分布上側5%分位數。

由表2中M值均小于其臨界值可知，上證指數收益率與滯后一個交易日的成交額變動率即（Ushb，Vsha）的聯合分布，可由權重分別為0.4969與0.5031的Clayton Copula和Frank Copula組成的混合Copula函數表出；深成指收益率與滯后一個交易日的成交額變動率間即（Uszb，Vsza）的聯合分布，可由Gumbel Copula、Clayton Copula和Frank Copula三者組成的混合Copula函數表出，權重分別為0.4507、0.3063及0.2430。

兩組變量的經驗頻率分布及所估計模型頻率分布分別見圖1、圖2與圖3、圖4。

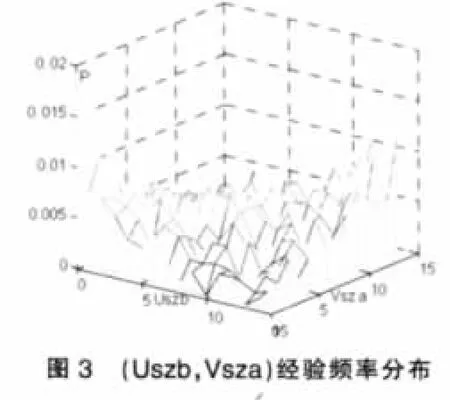
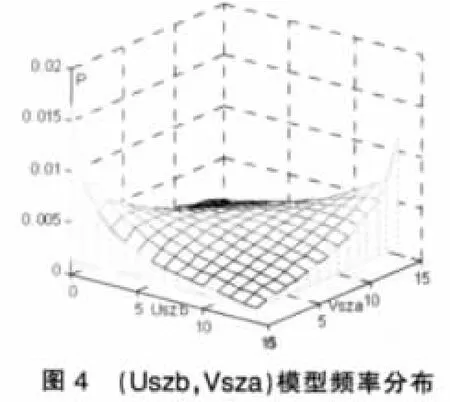
綜上，滬、深股市收益率與滯后一個交易日的成交額變動率間的聯合分布，可由混合Copula函數表出，因此可以判定滬、深股市收益率對成交額變動率具有先導作用。此外，收益率與滯后一個交易日的成交額變動率間的相關模式為尾相關：由圖1、圖2及圖3、圖4可以看出，聯合頻率在二者同時取較大值或較小值時，即其上、下尾部，較高，且下尾部的頻率稍高于上尾部的；二者之一取較大值而另一取值較小時很低。這意味著，股指漲幅較高時，下一交易日的成交額將相對擴大的可能性很高；股指跌幅較大時，下一交易日的成交額將相對萎縮的可能性非常高，且股指下跌后成交額萎縮的可能性稍高于指數上漲后成交額擴大的可能性。

根據以上分析，股指上漲后，股民熱情參與，“追漲”行為表現比較突出；股指下跌后，股民表現謹慎，進一步“殺跌”行為不明顯。這與一般認為我國股民慣于“追漲殺跌”不完全相同，但與“牛市成交量大，熊市成交量小”這句諺語相吻合。

2.2.2 成交額變動率對收益率的引導關系檢驗

為檢驗滬、深股市成交額變動率對收益率的引導關系，我們分別取Vsh、Vsz的前2534個值作為新序列Vshb、Vszb；取Ush、Usz的后2534個值作為新序列Usha、Usza，并組成兩對：（Usha，Vshb）及（Usza，Vszb），采用Copula分析法分別進行研究。

應用偽極大似然法估計Copula參數，經計算發現所有參數都不具有顯著性，結果在此不贅述。另外，觀察（Usha，Vshb）及（Usza，Uszb）的經驗頻率分布圖，見圖5、圖6，發現兩組變量均有可能相互獨立，為此驗證其獨立性如下。

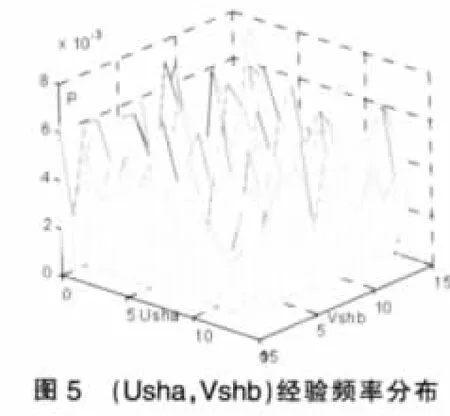
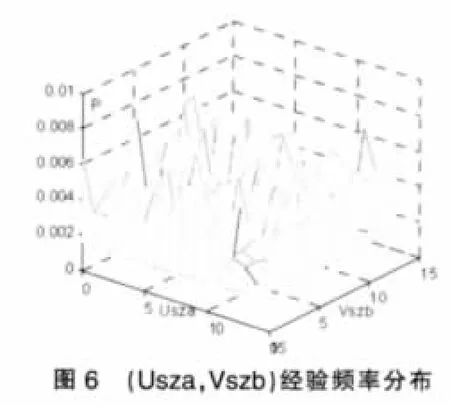
我們依然采用χ2擬合優度檢驗法，將區域[0，1]×[0，1]劃分為15×15個單元格。此時，令，p=1，2，，…，15；q=1，2，…，15。經計算變量（Usha，Vshb）及（Usza，Vszb）的M值分別為：221.6012、190.8864，二者皆小于自由度為196的χ2分布的上側5%分位數229.6632。因此可以判定Usha與Vshb及Usza與Vszb均相互獨立，即滬、深股市成交額變動率對下一交易日的收益率不存在引導關系。

2.2.3 收益率對滯后其兩個交易日成交額變動率的引導關系檢驗

由前面結論知，滬、深股市收益率對滯后一個交易日的成交額變動率具有先導作用，那么其對滯后兩個交易日的成交額變動率是否也有先導作用呢？下面對此進行檢驗。

分別取Ush、Vszaa的前2533個值作為新序列Ushbb、Uszbb；取Vsh、Vsz的后2533個值作為新序列Vshaa、Vszaa，并組成兩對：（Ushbb，Uszbb）及（Uszbb，Uszaa）。

觀察（Ushbb，Vshaa）及（Uszbb，Vszaa）的經驗頻率分布圖，即圖7與圖8，發現兩組變量均可能相互獨立，下面驗證其獨立性。

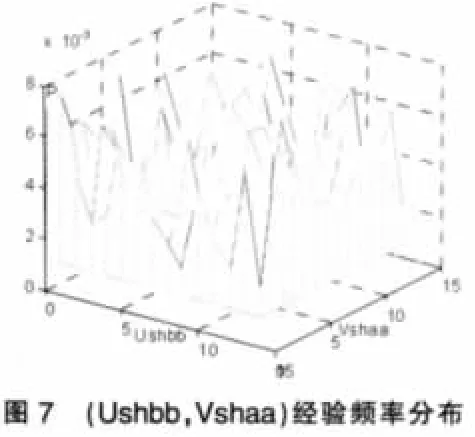
仍然采用前面驗證獨立性時的χ2擬合優度檢驗法。經計算，變量（Ushbb，Vshaa）及（Uszbb，Vszaa）的M值分別為：225.8956及180.1078，二者均小于臨界值229.6632。由此可知，滬、深股市收益率對滯后兩個交易日的成交額變動率不具有先導作用。

3 結論

本文基于滬、深股市日交易數據，借鑒在風險研究領域中應用廣泛的Copula分析法，研究了收益率與成交額變動率間的相互引導關系。結論顯示，成交額變動率與滯后其一個交易日的股指收益率間不存在引導關系；股指收益率對滯后其一個交易日的成交額變動率存在先導作用，不過這種先導作用對滯后其兩個交易日的成交額變動率不存在。

此外，股指收益率與滯后其一個交易日的成交額變動率間的相關模式表現為尾相關：其聯合頻率在二者同時取較大值或較小值時，即其上、下尾部，較高，且下尾部的頻率稍高于上尾部的；在二者之一取較大值而另一取值較小時很低。這意味著，股指漲幅較高時，下一交易日的成交額將相對擴大的可能性很高；股指跌幅較大時，下一交易日的成交額將相對萎縮的可能性非常高，且股指下跌后成交額萎縮的可能性稍高于指數上漲后成交額擴大的可能性。據此可知，股指上漲后，股民熱情參與，“追漲”行為表現比較突出；股指下跌后，股民表現謹慎，進一步“殺跌”的行為不明顯。這與“牛市成交量大，熊市成交量小”這句諺語相吻合，但與一般認為的我國股民慣于“追漲殺跌”不完全相同，我們認為我國股民慣于“追漲”，但“殺跌”只在股價上升一段后的反轉之初，即獲利盤較多時，有所表現；在股價已有一定跌幅，被套牢時，股民則傾向于捂盤待漲。

本文結論及芮萌，孫彥叢，王清和（2003）[4]、董秀良,吳仁水（2008）[6]基本結論均認為成交額或成交量對股指收益率沒有引導作用，與“量在價先行”相矛盾，這是否是中國股市所獨有的特性，有待于進一步基于個股及不同周期的數據進行驗證。

[1]HiemstraC，JonesJD.TestingforLinearandNon-linear Granger Causality in the Stock Price-volume Relation[J].Journal of Finance,1994,54(5).

[2]Silvapulle P，Choi J S.Testing for Linear and Non-linear Granger Causality in the Stock Price-volume Relation:Korean Evidence [J].The Quarterly Review of Economic and Finance,1999,39(1).

[3]魏巍賢,康朝鋒.上海股市價量關系的實證分析[J].預測,2001，（8）.

[4]芮萌,孫彥叢,王清和.中國股票市場交易量是否包含預測股票收益的信息研究[J].統計研究，2003，（3）.

[5]張博.上海證券A股市場價量關系實證研究[J].財經問題研究，2008，（2）.

[6]董秀良,吳仁水.交易量適合作為股價波動信息的代理變量嗎?[J].數量經濟技術經濟研究,2008，（1）.

[7]Sklar A.Fonctions de Repartitionàn Dimensions et leurs Marges [J].Publication de l'Institut de Statistique de l'Universitéde Paris, 1959，(8).

[8]Nelsen R B.An Introduction to Copulas[M].New York:Springer, 1998.

[9]羅俊鵬.Copula理論及其在金融分析中的應用研究[D].天津：天津大學理學院，2005.

[10]韋艷華.Copula理論及其在多變量金融時間序列分析上的應用研究[D].天津：天津大學管理學院，2004.

（責任編輯/浩天）

F830.9

A

1002-6487（2011）05-0141-04

南開大學基本科研業務專項資金項目（NKZXB10052）

吳明華（1982-），女，博士研究生，研究方向：資本市場及金融工程。

周愛民（1961-），男，教授，博士生導師，研究方向：資本市場及金融工程。