灰色PERT算法在項目工期中的研究與應用

符長虹，吳順祥，王文淵

（1.廈門大學自動化系，福建廈門361005；2.中國中鐵四局集團有限公司，合肥230023）

灰色PERT算法在項目工期中的研究與應用

符長虹1，吳順祥1，王文淵2

（1.廈門大學自動化系，福建廈門361005；2.中國中鐵四局集團有限公司，合肥230023）

為提高PERT網絡中關鍵路線與關鍵工序決策的可靠性，減少求解的復雜性，文章根據工序時間不確定的特點，結合灰色系統理論，提出了工序時間為區間灰數的灰色PERT網絡，并且根據實際工序時間概率分布的特點，提出了工序時間的正態分布模型，該方法避免了決策中片面采用均勻分布區間灰數描述模糊評價的局限性，更好地體現了工序“最可能時間”、“最悲觀時間”與“最樂觀時間”三者概率分布的特點。另外，考慮到工程計劃能否在規定工期內順利完成這一隨機現象，提出了相應的灰色PERT算法。最后，通過實例分析，說明該灰色PERT算法能夠有效避免片面采用均勻分布區間灰數的局限性，且計算出項目工程在規定工期內完成的可能概率，更加符合實際項目工期的決策，具有較好的可行性和高效性，拓展了這一領域的研究與應用。

PERT網絡；灰色理論；均值白化值；正態分布；標準差；關鍵路線

0 引言

考慮到經典PERT網絡中工序完成時間受許多內、外諸因素影響，導致其具體數值無法確定，只能通過估計最樂觀時間a、最可能時間m與最悲觀時間b來進行關鍵路線與關鍵工序的決策，然而本文結合灰色系統理論，基于工序完成時間在區間[a,b]內變化的特點，提出了工序完成時間為區間灰數的灰色PERT網絡。但是根據經典PERT網絡中三種估計時間概率分布的特點，文獻[1]等的工序完成時間片面采用均勻分布區間灰數來描述模糊評價的方法則會產生嚴重的失真，因此本文針對這個局限性，考慮到三種估計時間近似服從正態分布的特點，提出了工序完成時間服從正態分布的分布模型。文獻[2]等的PERT網絡中忽略了每一條路線在規定項目工期內實際完成該項目的“可能性”這一隨機現象，因此本文為更全面、更科學、更有效地研究PERT網絡，提出了相應的灰色PERT算法，該算法通過求出每項工序完成時間區間灰數的均值白化值以及標準差，接著求出每條線路上所有工序完成時間區間灰數的均值白化值之和以及標準差，進而求出每條線路上所有工序完成時間區間灰數的均值白化值之和所對應的概率系數以及在規定工期內完成項目的概率，最后根據概率的大小決策關鍵線路與關鍵工序，通過實例分析，說明該灰色PERT算法具有較好的可行性和高效性，減少了信息失真與決策失誤。

1 基本理論

2 灰色PERT網絡及其關鍵線路與關鍵工序的確定

2.1 灰色PERT網絡及工序時間概率模型的研究

考慮到經典PERT網絡通過三種估計時間，即最樂觀時間a、最可能時間m與最悲觀時間b，來決策關鍵線路與關鍵工序，結合灰色系統理論以及工序完成時間在最樂觀時間與最悲觀時間之間變化，即在[a,b]之間變化，本文介紹工序完成時間為區間灰數的灰色PERT網絡，如圖1所示，其中對應的工序時間灰數為hi(茚)∈

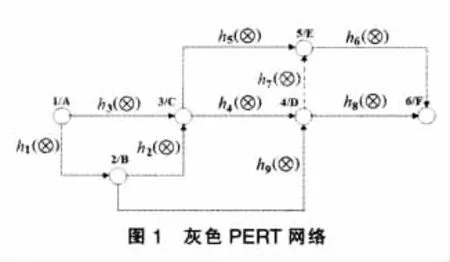
本文又考慮到經典PERT網絡中三種估計時間的概率分布情況，根據實際情況，工序完成時間區間灰數不可能片面認為服從均勻分布，這會造成決策的嚴重失真，因此提出了基于正態分布的工序完成時間，如圖2所示[3][4]。

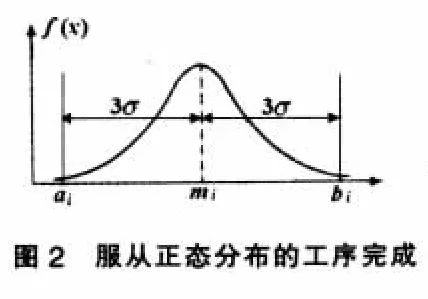
由圖3可知，本文可以確定正態分布的參數，其中正態分布的數學期望根據正態分布3σ的原則，即p (x∈[ai,bi])=0.997，可得方差

2.2 關鍵線路與關鍵工序的確定

在灰色PERT網絡中,考慮到項目計劃能否在規定工期內完成項目這一隨機現象，本文結合灰色理論，利用各條線路上所有工序完成時間區間灰數的均值白化值之和所對應的概率，來進行關鍵路線以及關鍵工序的決策，具體的灰色PERT網絡算法步驟如下：

步驟1在灰色PERT網絡中，找出所有的路線，記為xi(i=1,2,…,n)，以及第xi條線路上的工序，其時間灰數分別記為(j=1,2,…,m)，其中hij(茚)表示第xi條線路上第j道工序的時間灰數；

步驟2計算出灰色PERT網絡中各個工序時間灰數的均值白化值hi(茚軜)以及對應的方差σi，并分別計算出第xi條線路上所有工序時間灰數的均值白化值hi(茚軜)之和以及標準差：

其中，σxi表示第xi條線路上項目完成時間的標準差；

步驟3根據規定的項目計劃總工期T，分別計算出每條路線上所有工序時間灰數的均值白化值hi(茚軜)之和的概率系數：

步驟4根據公式（3）計算出的概率系數分別計算每條線路在所有工序時間灰數的均值白化值hi(茚軜)之和下完成該項目的概率：

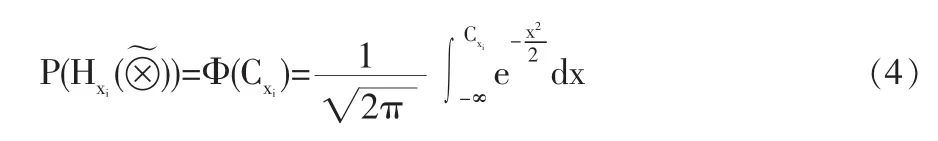
步驟5對公式（4）求得的概率進行排序，其中概率最小所對應的路線則為關鍵路線，其上的工序則為關鍵工序。

3 實例分析

某實際項目中共有9道工序，每項工序的持續時間如表1所示[1][2]。

表1 各工序的持續時間

表1所對應的灰色PERT網絡如圖3所示。

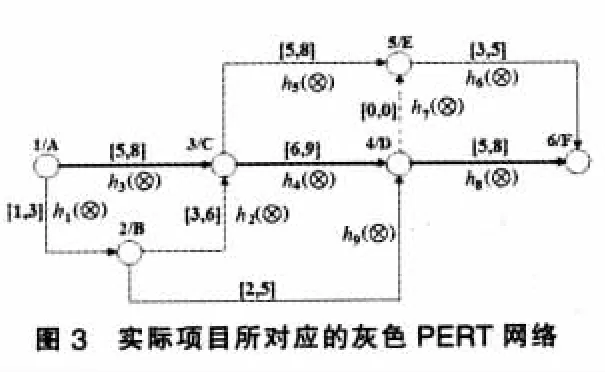
步驟1該灰色PERT網絡中共有5條線路，分別如下：

第x1條：1→3→5→6，共3項工序：h3(茚)、h5(茚)和h6(茚)，分別記為h11(茚)、h12(茚)和h13(茚)；

第x2條：1→3→4→5→6，共4項工序：h3(茚)、h4(茚)、h7(茚)和h6(茚)，分別記為h21(茚)、h22(茚)、h23(茚)和h24(茚)；

第x3條：1→3→4→6，共3項工序：h3(茚)、h4(茚)和h8(茚)，分別記為h31(茚)、h32(茚)和h33(茚)；

第x4條：1→2→3→4→6，共4項工序：h1(茚)、h2(茚)、h4(茚)和h8(茚)，分別記為h41(茚)、h42(茚)、h43(茚)和h44(茚)；

第x5條：1→2→4→6，共3項工序：h1(茚)、h9(茚)和h8(茚)，分別記為h51(茚)、h52(茚)和h53(茚)。

步驟2計算各個工序時間灰數的均值白化值hi(茚軜)以及對應服從正態分布的方差σi：工序1→2：其工序持續時間區間灰數為h1(茚)∈[1,3]，

同理，其余工序持續時間，期望以及方差如表2所示。

表2 其余各個工序持續時間灰數的均值白化值以及方差

根據公式（1）計算出各條線路上所有工序時間灰數的均值白化值hi()之和（見表3）。

表3 各線路上所有工序時間灰數的均值白化值之和

根據公式（2）計算每條線路上項目完成時間的標準差如下：

同理可以求得其余線路的標準離差：

σx2=0.782,σx3=0.866,σx4=0.928,σx5=0.782

步驟3根據公式（3）計算在規定項目計劃總工期為T= 20的情況下各條線路所對應的概率系數：

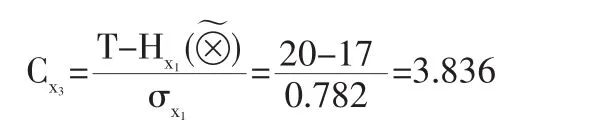
同理可求得其余路線上所對應的概率系數（見表4）。

表4 其余路線所對應的概率系數

表5 其余線路所對應的概率

步驟4根據公式（4）求得各條路線上所有工序時間灰數的均值hi()白化值之和的概率：

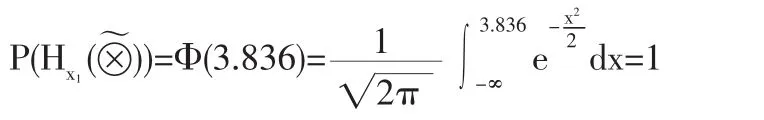
同理可求得其余路線上所對應的概率：

步驟5根據步驟4求得的各路線對應概率進行排序，其中概率最小對應的路線即為所求關鍵路線：故有關鍵路線為x3：1→3→4→6，如圖3中粗線所示。

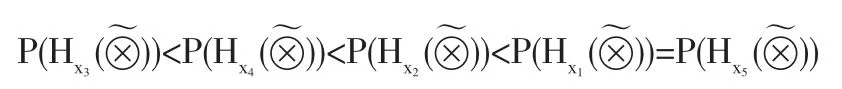
4 結論

本文針對決策中采用均勻分布區間灰數描述模糊評價值的局限性，考慮到正態分布模型能夠更準確、更有效表示工序完成時間的概率分布特點，以及項目計劃是否能在規定工期內完成項目的可能性這一隨機現象，提出了應用正態分布區間灰數來決策灰色PERT網絡中關鍵路線與關鍵工作的算法。通過實例證明，該方法具有較好的可行性和高效性，為這一領域提供了關鍵路線以及關鍵工序決策的新方法，可供從事PERT網絡的技術人員與管理人員參考。

[1]崔邯龍，李萬慶，孟文清.張艷杰，灰色網絡計劃中的關鍵線路確定方法研究[J].數學的實踐與認識，2009，38(8).

[2]楊應玖，楊毅，楊念.論灰色網絡計劃技術[J].武漢水利電力大學學報，1998,31(3).

[3]謝乃明，劉思峰.考慮概率分布的灰數排序方法[J].系統工程理論與實踐，2009，29(4).

[4]劉琳，陳云翔，葛志浩，基于正態分布區間數的概率測度及多屬性決策[J].系統工程與電子技術，2008,30(4).

[5]Chao-Chin Chung,Ho-Hsien Chen,Pao-Chuan Hsieh.Optimization of the Monascus Purpureus Fermentation Process Based on Multiple Performance Characteristics[J].Journal of Grey System,2008, 11(2).

[6]Wen-Fang Hsieh,Kun-Li Wen.A New Approach of Grey Decision-Making[J].Journal of Grey System,2009,12(2).

[7]Guo-Dong Li,Daisuke Yamaguchi,Masatake Nagai,Masatoshi Kitaoka.A Research on Grey Model by Grey Interval Analysis[J]. Journal of Grey System,2006,9(2).

[8]Ping-Yi Hu.Using A Grey Multipurpose Decision System for Car Purchasing[J].Journal of Grey System,2004,7(1).

[9]Long-qing Shen,Jian-feng Yu,Hai-wei Yang.Research on Algorithms for Critical Path of PERT Network with Lowering Conditions[J].Application Research of Computers,2006,(1).

[10]劉思峰，黨耀國，方志耕.灰色系統理論及其應用[M].北京：科學出版社，2004.

（責任編輯/易永生）

F224

A

1002－6487（2011）05－0152-03

國家自然科學基金資助項目（60704042）；國家“十一五”科技支撐計劃項目（2007BAK34B04）

符長虹(1986-)，男，湖南岳陽人，碩士，研究方向：不完備系統與數據挖掘。

吳順祥（1966-），男，湖南邵陽人，博士，教授，研究方向：不完備系統。

王文淵（1985-），女，河南雞西人，助理工程師，研究方向：工程設計。